こんにちは!今回も化学のための数学の続きをやっていきます。今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(permutation)
行列を深く理解するための準備的な内容なのでこの動画だけだとあまり面白くないかもしれませんが、大事なことなのでどうかお付き合いください。
では参りましょう!
置換とは
まず、置換がどんなものかというと、\(n\)個の整数からなる集合から自身への1対1写像のことを言います。
写像とか言われても分かんないんで例で説明しましょう。
例えば次数が\(3\)、つまり\(1\)、\(2\)、\(3\)が並んでいる中で\(1\)と\(2\)を入れ替えるという操作を行う事にします。
そしてこの操作のことを置換と呼びましてこんな形で表現します。
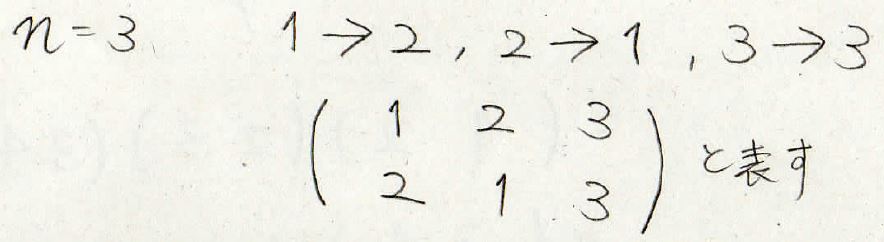
2段になっていて上の行には\(1\)、\(2\)、\(3\)という風に順番に数字を書きます。
そして下の行には入れ替えを行った後の数字の並びを書きます。
この例であれば\(1\)と\(2\)を入れ替えるという操作をしているので\(1\)の下に\(2\)が来て、\(2\)の下に\(1\)が来るという事になります。
これを一般化すると\(1\)が移される先が\(k_1\)、\(2\)が移される先が\(k_2\)ということになるのでこのように書くことができます。
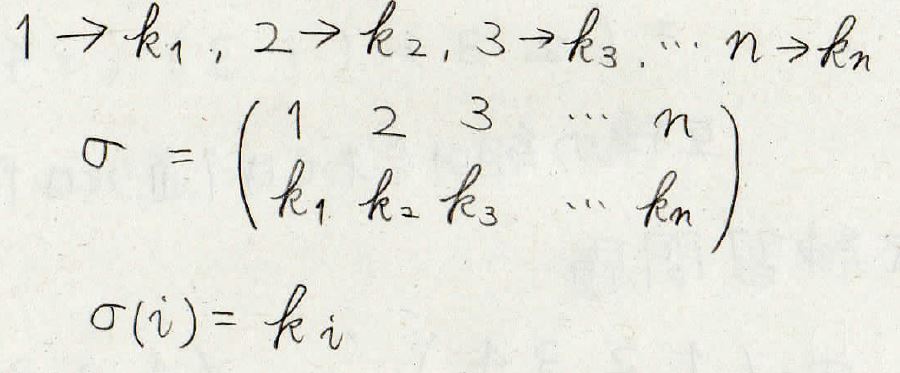
この置換を\(\sigma\)として表すことにすると\(i\)が移される先は\(\sigma (i)\)で表現できます。
そしてこの置換は数に限りがありまして、次数が小さいほど少なくなります。
例えば\(1\)次の置換はそのままにするという操作しかないため1個しかありません。
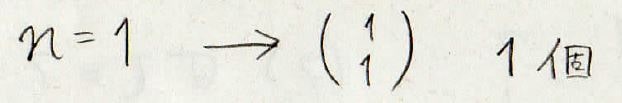
\(2\)次の置換はそのままにするか、\(1\)と\(2\)を入れ替えるかという2個が出てきます。
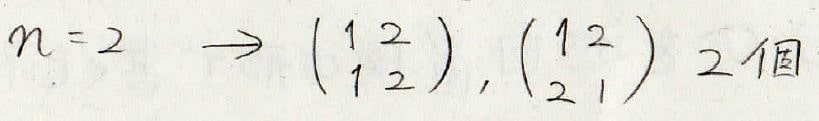
そして\(3\)次の場合はこの通り6個の置換が存在します。
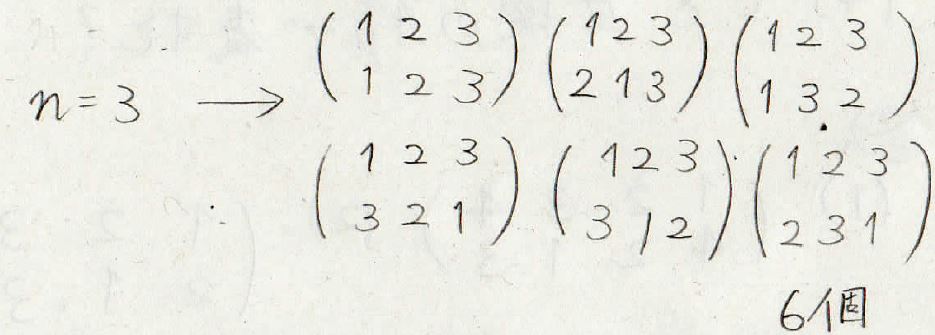
ここで勘の良い人は分かると思いますが、取り得る置換の個数はその次数の階乗になります。
置換の掛け算
それで、ここからは置換の掛け算をどう考えるのかという話をします。
次数が同じ2つの置換\(\sigma\)と\(\tau\)について、\(\sigma \tau\)の\(i\)が移される先は\(\sigma (\tau (i))\)になります。

実際の例でやってみますとこんな感じです。
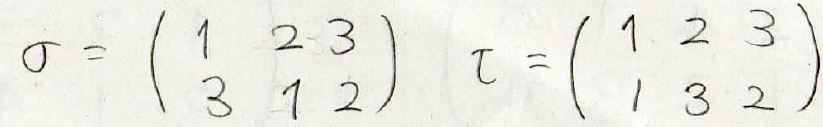
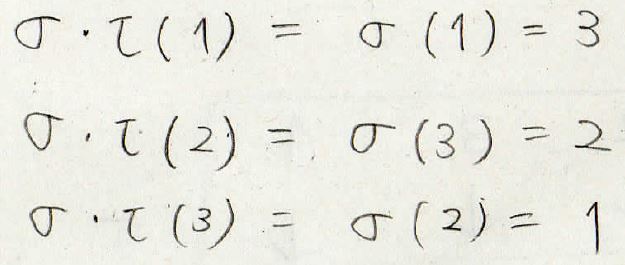
\(\sigma (\tau (1))\)を考える際にはまず\(\tau (1)\)を見ます。
すると\(1\)になるので、今度は\(\sigma (1)\)を見て、\(3\)になります。
\(\sigma (\tau (2))\)については、まず\(\tau (2)\)が\(3\)なので\(\sigma (3)\)を見ればいいことになり、\(2\)が出てきます。
そして、\(\sigma (\tau (3))\)は余った\(1\)になります。
単位置換
では続いて単位置換というものについてお話しします。
これは言葉で説明するとそのままにしておくという操作のことです。
すなわち、上の段の数字と下の段の数字が全て同じになっている置換が単位置換となります。

そしてある置換に対して掛け算をすることで単位置換になる置換のことを逆置換といいます。
そして逆置換との掛け算では順番を交換することもできます。
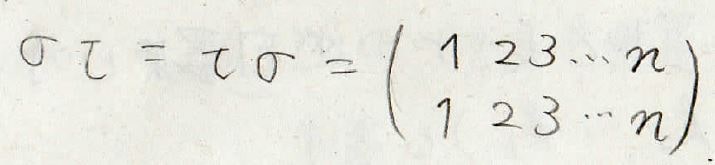
一般的にこのような置換の掛け算は交換できないので知っておいてください。
試しにさっき出てきた\(\sigma\)と\(\tau\)を使って\(\tau \sigma\)を出してみると\(\sigma \tau\)と一致していません。
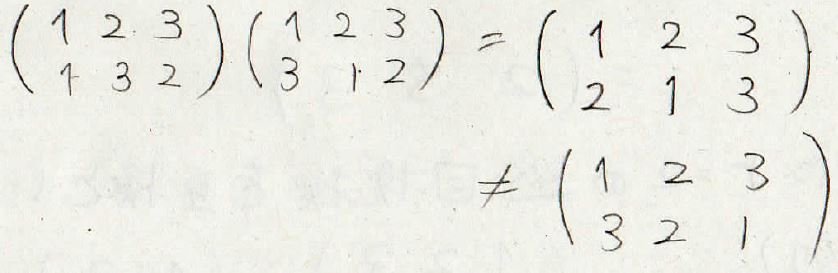
逆置換の求め方
逆置換はこんな風にして求めます。
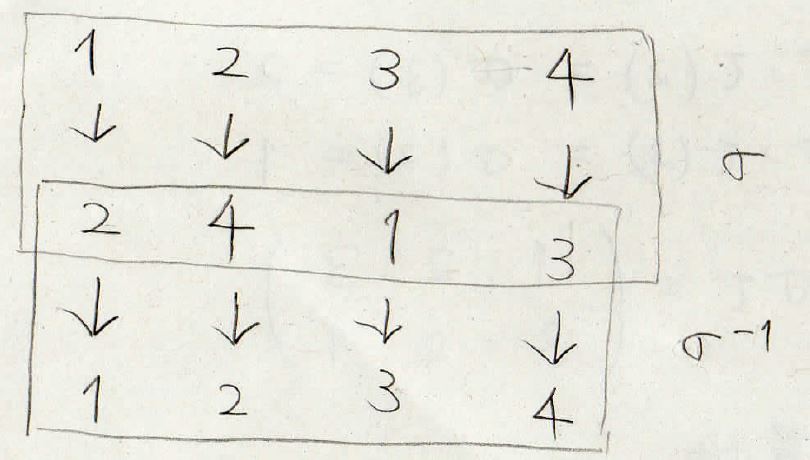
まず、\(\sigma\)の上の段と下の段を入れ替えて書きます。

そのあと、上の段が\(1\)、\(2\)、\(3\)、\(4\)と順番になるように並び替えるだけです。
模式的に書けばこんな感じになります。
巡回置換
さあ、では今度は巡回置換というものについてお話しします。
色々出てきて大変ですがもうちょっとなのでお付き合いください(笑)
巡回置換とはある値から始まり移った先の値を見て、その値が今度どこに移るのかというのが一周するまでつなげていきます。
そこで出てこなかった値は固定して、出てきた値だけを順番に並べたものが巡回置換となります。
そのとき出てきた値の個数を長さと言います。
全くもってなんのこっちゃなんで例を見てみましょう。
\(\sigma\)がこんな置換だったとします。
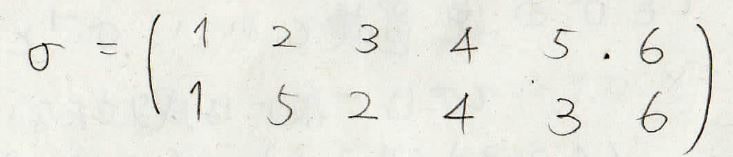
ここで、\(1\)、\(4\)、\(6\)は上下が同じで固定されています。
そして違う値へ移っている中でまず\(2\)に注目してみましょう。
\(2\)は\(5\)に移されています。
そうしたら今度は\(5\)の移り先に着目します。\(5\)は\(3\)に移っています。
そして、また\(3\)に着目してみると、\(3\)の移り先は\(2\)になっていて一周してしまいました。
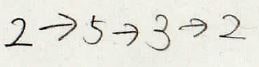
そして、この場合には出てきた値を順番に並べて\((2 5 3)\)と表記します。
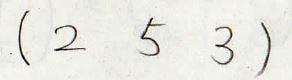
これが巡回置換です。この場合の長さは\(3\)になります。
互換
そして特に長さが\(2\)の巡回置換のことは互換と呼ばれます。
長さが\(2\)という事は単純に2つの値を入れ替えたという操作になります。
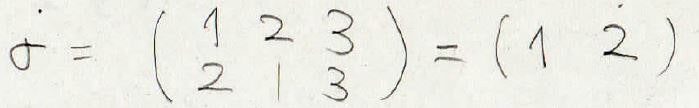
そして、これが行列を理解するうえでもポイントになるので覚えておいてほしいんですけど、任意の置換は互換の積という形で表現することができます。
例えばこの\(\sigma\)を互換の積の形にすると\((1 2)(2 3)(3 4)\)となります。
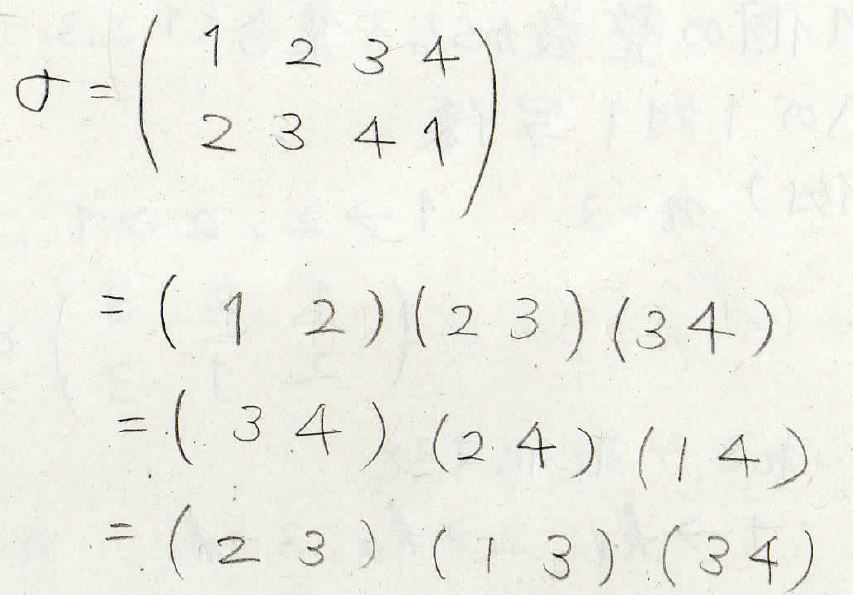
また、どこから入れ替えてもいいので、\((3 4)(2 4)(1 4)\)や\((2 3)(1 3)(3 4)\)なども\(\sigma\)と同じ意味になります。
こんな風に互換の積としての書き換えは1通りとは限らないので、覚えておいてください。
練習問題
はい、それでは本題は以上ですので練習問題をやってみましょう!
\(\sigma\)と\(\tau\)を下のように与えられるとき、\(\sigma ^{-1}\)、\(\sigma \tau\)、\(\sigma\)の巡回置換としての表記、\(\tau\)の互換の積としての表記をそれぞれ求めてくださいという問題です。

こんな感じになってますので、間違っていた方はじっくり考えてみてください。
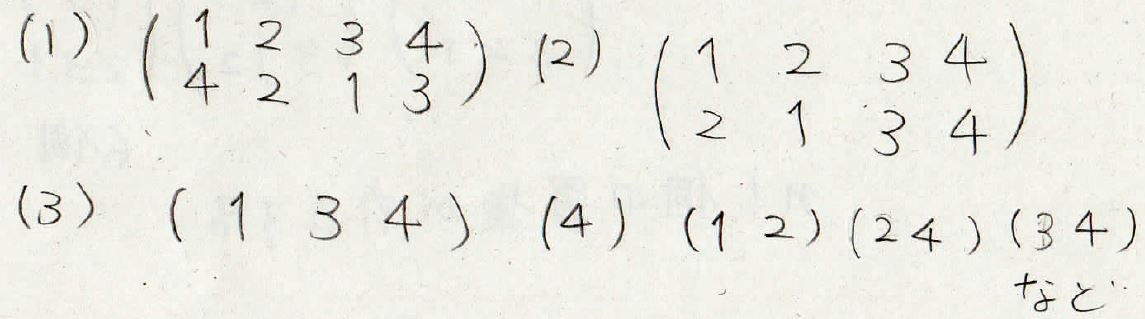
まとめ
それでは最後軽くおさらいをやって終わります。
まず置換とはそれぞれの値がどこに移されるのかを表したもので、その次数の階乗の数だけ考えることができます。
そして置換の掛け算はまず、右側の移り先を考えたのちに左側の置換によってその移り先がまたどこに移るかを考えます。
そして、置換の中にはそのまま移すという単位置換があるんですけど、ある置換に対して掛け算をすると単位置換になるものを逆置換と呼び、これは元の置換の上下を入れ替えることにより求めることができました。
そして、巡回置換というのは移った先の値がどこに移るのかというのを一周するまで考えて辿った値を書くことで表現します。
その際、辿った中に出てこなかった値は固定されている物だと考えます。
出てきた値の個数は長さと呼ばれ、特に長さが\(2\)、すなわち2つの値を入れ替えるという巡回置換は互換と呼ばれます。
任意の置換は互換の積という形で表現できます。
また、その時の表し方は1通りであるとは限らなくて、多くの場合は複数あります。
それではどうもありがとうございました!



