こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(chirality)
異性体の分類
まずは、化学で出てくる異性体の分類について、改めて確認したいと思います。
そもそも異性体とは、分子式は同じだが構造が異なる物質のことを言います。
構造異性体と立体異性体に大別でき、これらもまたいくつかの種類に分かれます。
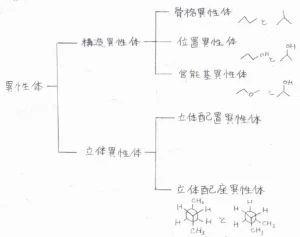
構造異性体
まず、構造異性体とは、分子式が同じで、原子の繋がり方がことなる物質のことで、さらに骨格異性体(連鎖異性体)、位置異性体、官能基異性体に分類できます。
骨格異性体(連鎖異性体)
骨格異性体とは、分子の炭素骨格が異なる物質のことです。
例えば、n-ブタンと2-メチルペンタンの関係がこれに該当します。
位置異性体
2つ目の位置異性体とは、分子の炭素骨格は同じですが、官能基が結合している位置に違いがある物質のことです。
例えば、1-プロパノールと2-プロパノールの関係が該当します。
官能基異性体
3つ目の官能基異性体とは、分子式は同じものの、官能基の種類が異なる物質のことを言います。
例えば、メトキシメタンと2-プロパノールは、どちらの分子式も\(\displaystyle \rm{C_3H_8O}\)\(\)ですが、一方はエーテル、もう一方はアルコールに分類される化合物です。
これらは、水への親和性、沸点、起こりうる化学反応などにおいて、まったく異なる性質をもちます。
立体異性体
一方で、構造異性体に含まれない異性体である立体異性体とは、分子式と原子の繋がり方が同じだが原子の空間的な配置に違いがある物質のことを言います。
立体異性体は、さらに立体配置異性体と立体配座異性体に分けることができます。
立体配座異性体
立体配座異性体とは、単結合のまわりの回転により相互交換できる関係にあるものを指し、これらは同一の化合物として扱われます。
そのため、厳密には他の異性体と意味が違います。
前回お話しした、n-ブタンのトランス型とゴーシュ型の立体配座どうしの関係がこれに該当します。
立体配置異性体
一方の立体配置異性体は、立体異性体のうち単結合の回転では相互交換できないものということになります。
立体配置異性体は、さらにエナンチオマー(光学異性体、鏡像異性体)とジアステレオマーに分類でき、ジアステレオマーも、シス-トランス異性体(幾何異性体)と立体化学的ジアステレオマーの2つに分けられます。
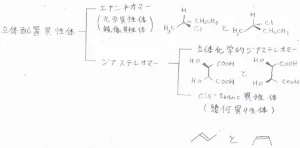
エナンチオマー(光学異性体、鏡像異性体)
まず、エナンチオマーとは、鏡写しの関係になっているものを言います。
ここには、互いにエナンチオマーの関係である2種類の2-クロロブタンの構造を書いています。
エナンチオマーの関係にある2つの化合物は、同じ対称性をもつため、結晶の安定性や分子間力も等しくなります。
その結果、沸点、融点、密度など基本的な物性はすべて同じになります。
ただし、生物の体内など、キラルな環境下では異なる応答を示す場合があります。
ジアステレオマー
一方で、ジアステレオマーとは、立体異性体のうち、単結合の回転でも相互交換できず、鏡写しの関係にもない物質を指します。
対称性が異なるため、一般的にジアステレオマーどうしで沸点、融点、密度などは一致しません。
シス-トランス異性体(幾何異性体)
シス-トランス異性体は、二重結合や環構造といった回転が束縛された構造をもち、官能基の相対的な位置関係が異なるものを指します。
trans-2-ブテンとcis-2-ブテンがその例です。
立体化学的ジアステレオマー
それに該当しないものが立体化学的ジアステレオマーと言われるものです。
ここには、立体化学的ジアステレオマーの関係にある2種類の酒石酸という化合物の構造を書いています。
キラリティ
ここからは、先ほどの異性体の分類のうち、立体配置異性体に関して、さらに考えていきます。
\(\displaystyle \rm{sp}\)\(^3\)混成の炭素原子に結合している4つの置換基がすべて異なるとき、その炭素原子のことを不斉炭素と言います。
不斉炭素を1つだけもつ化合物には、必ずエナンチオマーが存在します。
例えば、下図上側の化合物では、炭素原子に結合している4つの置換基のうち、2つが水素で共通しているので、この分子は不斉炭素をもっておらず、エナンチオマーは存在しません。
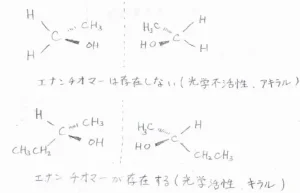
エナンチオマーが存在しないことは、光学不活性である、またはアキラルであると言います。
この場合、鏡に映した構造は、回転させて元の構造と重ねられるので、同一の化合物だと言えます。
そして、上図下側の化合物では、4つの置換基がすべて異なるので、中心の炭素原子が不斉炭素であり、この化合物にはエナンチオマーが存在することになります。
鏡に映した構造をいくら回しても元の構造とは一致しないので、これらは別の化合物であると言えます。
エナンチオマーが存在することは、光学活性である、またはキラルであると言います。
分子や物体がその鏡像と重ね合わせることができない性質のことは、キラリティと言います。
そして、より一般的には、構造の中に対称面があるかどうかでキラリティの判別ができます。
例えば、先ほどアキラルな化合物として例に挙げたエタノールは、図の中で赤で示した平面について、対称な構造をしています。

一方で、キラルな分子である2-ブタノールでは、対称面を見つけることができません。
不斉炭素が2つ以上の場合でも、この方法でキラルかどうかを判定できます。
ここでは、2つの不斉炭素をもつ化合物についてお話しします。
下記の構造式において、\(\displaystyle \rm{X}\)\(\)、\(\displaystyle \rm{Y}\)\(\)、\(\displaystyle \rm{Z}\)\(\)および\(\displaystyle \rm{X’}\)\(\)、\(\displaystyle \rm{Y’}\)\(\)、\(\displaystyle \rm{Z’}\)\(\)は互いに異なる置換基を表しています。
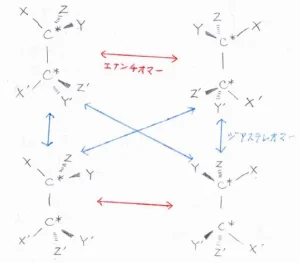
不斉炭素を1つにつき2通りの立体配置があると考えると、4つの立体配置異性体を考えることができます。
両方の不斉炭素について異なる立体配置となっているものどうしは、エナンチオマーとなります。
一方の不斉炭素についてのみ異なる立体配置となっているものどうしでは、鏡写しではないので、ジアステレオマーとなります。
ただし、2つの不斉炭素に結合している3つの異なる置換基が同じ組み合わせの場合、すなわち\(\displaystyle \rm{X=X’}\)\(\)、\(\displaystyle \rm{Y=Y’}\)\(\)、\(\displaystyle \rm{Z=Z’}\)\(\)のときには、この図のようにジアステレオマーの一方が面対称となります。
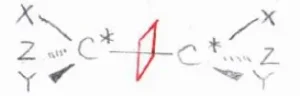
この化合物は、鏡像をとっても回転させれば元の構造と重なるので、同じ化合物です。
このように、不斉炭素をもっているが、アキラルとなる化合物のことは、メソ体と言います。
旋光性
ここからは、エナンチオマーをどのように区別するのかという話をします。
先ほどもお話ししたとおり、エナンチオマーは融点、沸点、密度など物理的な性質がまったく同じになりますが、偏光に対する応答には違いが生じます。
具体的には、キラルな物質の溶液に直線偏光を通過させると、電場の振動の向きが変化する旋光という現象が起こります。
この現象は、複屈折の一種であり、キラルな化合物の非対称な電子分布が溶液全体で平均化されないときに起こる現象です。
反応条件が同じとき、互いにエナンチオマーの関係にある2種類の分子は、電場の振動の方向を逆方向へ同じ大きさだけ変化させます。
観測者が光源のほうに向かって、偏光面が右に傾くことを右旋性、左に傾くことを左旋性と言います。
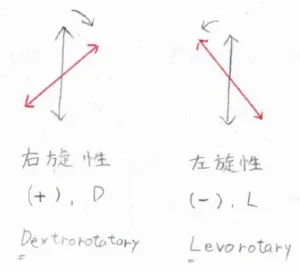
これらはをIUPAC名で区別するときには、それぞれ「(+)-」と「(-)-」を付けて、区別します。
また、それぞれの化合物をD体、L体と言って、区別することもあります。
生体内に存在するグリシン以外のアミノ酸は、そのほとんどがL体であることが知られています。
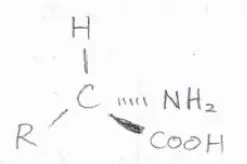
また、天然に存在する単糖は、そのほとんどがD体です。
エナンチオマーどうしで生体に対する応答に違いが生じうるのは、生体内が一部キラルな環境にあるためです。
ただし、どれだけ旋光面を変化させたのかという実測値は、その化合物の種類だけでなく、実験条件にも依存するので、単純に比較することはできません。
そこで、物質に固有の比旋光度\(\displaystyle [\alpha]_\lambda^t\)という値を用います。
その定義は、実測の旋光した角度\(\displaystyle \alpha\)を溶液の濃度\(\displaystyle c\)と試料セルの長さ\(\displaystyle l\)で割るというものです。
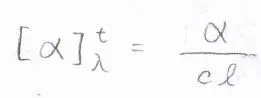
旋光度の実測値は、入射光が干渉した分子の個数に比例するため、比旋光度では、その要素を排除しています。
ただし、それ以外にも、温度や入射光の波長、溶媒の種類にも依存するため、文献等のデータと比較する場合には、これらの要素もそろえておく必要があります。
角度\(\displaystyle \alpha\)を度数法で表すことにして、濃度\(\displaystyle c\)の単位を\(\displaystyle \rm{g\ mL}\)\(^{-1}\)、セルの長さ\(\displaystyle l\)の単位を\(\displaystyle \rm{dm}\)\(\)としたとき、比旋光度\(\displaystyle [\alpha]\)の単位は、\(\displaystyle 10^{-1}\ \rm{deg\ cm^2\ g}\)\(^{-1}\)となります。
この単位は、しばしば省略されて、比旋光度が無次元量であるように表記されることもあります。
また、濃度\(\displaystyle c\)の単位を\(\displaystyle \rm{g\ dL}\)\(^{-1}\)として、\(\displaystyle [\alpha]_\lambda^t=\frac{100\alpha}{cl}\)としている文献もあります。
この旋光度測定の結果を使うと、2つのエナンチオマーが混ざっていたときに、その割合を算出することができます。
一方のエナンチオマーがどの程度過剰に存在しているかを表すときには、エナンチオマー過剰率(ee)という値を計算します。
これは、混合物の比旋光度を純粋な一方のエナンチオマーの比旋光度で除したものを百分率で表したもので、光学純度とも言われます。

例として、純粋なD体の比旋光度が\(\displaystyle 20.0\)、混合物の比旋光度が\(\displaystyle 15.0\)のときを考えると、そのエナンチオマー過剰率は、\(\displaystyle 75.0\%\)となります。

純粋なL体の比旋光度は\(\displaystyle -20.0\)で、D体のモル分率を\(\displaystyle x\)とすると、L体のモル分率は\(\displaystyle 1-x\)です。

これを方程式に当てはめると、\(\displaystyle x=\frac{7}{8}\)と計算されます。
つまり、D体とL体の存在比は\(\displaystyle 7:1\)だとわかります。
エナンチオマー過剰率は、あくまで旋光度の比なので、モル分率と混同しないでください。
エナンチオマー過剰率とモル分率の関係式は、次のように求められます。
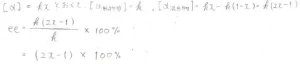
まず、各成分の比旋光度への寄与は、モル分率に比例するはずなので、その比例定数を\(\displaystyle k\)とおきます。
すると、純粋なD体については、モル分率が\(\displaystyle 1\)なので、その比旋光度は\(\displaystyle k\)と書けます。
L体のモル分率は\(\displaystyle 1-x\)、比旋光度の比例定数は\(\displaystyle -k\)となるので、混合物の比旋光度は\(\displaystyle kx-k(1-x)=k(2x-1)\)となります。
したがって、両者の比をとると、エナンチオマー過剰率が\(\displaystyle (2x-1)\times 100\%\)で与えられることがわかります。
エナンチオマーがちょうど\(\displaystyle 1:1\)で混合したものは、ラセミ混合物またはラセミ体と呼ばれますが、その場合のエナンチオマー過剰率は\(\displaystyle 0\%\)となります。
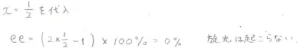
このとき、溶液内の局所的には旋光が起こっていますが、全体としては旋光は観測されず、光学不活性となります。
絶対配置による区別
以上が直線偏光の旋光によって、エナンチオマーを区別する方法の話でした。
しかし、この方法は実験事実に基づくものなので、未知の化合物やあまりにも不安定な化合物に対しては、どちらがD体なのか断定するのが困難なことがあります。
そこで、実験事実に基づかず、その絶対配置からエナンチオマーを区別する方法もよく使われます。
置換基に優先順位を付けて、それがどちらのパターンに当てはまるかを考えます。
置換基に優先順位を付けるルールは、次のとおりです。
まず、不斉炭素に直接結合している原子のうち、原子番号の大きいものから番号を付けます。
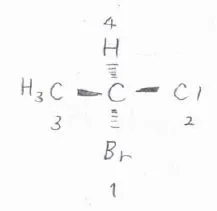
1-ブロモ-1-クロロエタンの場合、不斉炭素に直接している原子は、水素、炭素、塩素、臭素です。
これを原子番号の大きいほうから数えるので、ブロモ基が1、クロロ基が2、メチル基が3、水素が4となります。
原子番号が1の水素が結合している場合は、必ず優先順位が4番目になります。
そして、不斉炭素に直接結合している原子が同じ置換基については、末端側へとたどって、初めて違いが生じた原子の原子番号から番号を付けます。
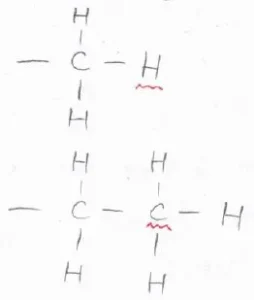
メチル基とエチル基を例にすると、不斉炭素中心に直接結合している原子は、どちらも炭素原子となりますが、その炭素原子に結合している原子の1つがメチル基は水素、エチル基は炭素となります。
炭素のほうが原子番号が大きいため、エチル基はメチル基よりも優先順位が高いことになります。
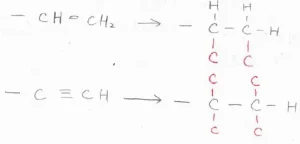
そして、置換基に二重結合や三重結合があった場合は、次のように扱います。
まず、エテニル基について、2つの炭素原子の二重結合を単結合に置き換えます。
次に、4本あるうちの残り1本の結合を、炭素原子との単結合として考えます。
先ほどのエチル基と比較すると、1位の炭素に結合している原子の1つが水素か炭素かで違いが生じるので、エテニル基のほうが優先順位が高いことになります。
同様に、エチニル基についても、まず三重結合を単結合に置き換えます。
残る2本ずつの結合は、炭素原子との単結合と考えます。
これをエテニル基と比較すると、エチニル基のほうが優先順位が高いことになります。
最後に、最も優先順位の低い置換基が奥側になるような方向から、その分子を見たときに、残る3つの置換基の配置がどうなるかを考えます。
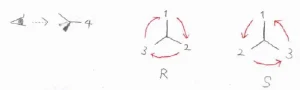
1、2、3番目の置換基を順番に数えたときに、時計回りになっているものをR体、反時計回りになっているものをS体と言って、エナンチオマーを区別します。
RとSの大文字を書いたときに、それぞれの曲線部分の書き始めが時計回りと反時計回りになっているので、それで覚えると便利です。

Fischer投影式
立体を考慮するとき、実線と波線とくさび型で単結合を表現する方法がありますが、R体とS体の判別には、Fischer投影式という表記法が便利です。
これは、不斉炭素に結合している4つの置換基を、十字で表したものです。
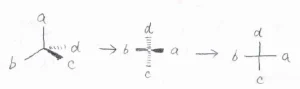
この例において、縦方向に書かれている置換基である\(\displaystyle c\)と\(\displaystyle d\)は紙面奥側に向いており、横方向に書かれている\(\displaystyle a\)と\(\displaystyle b\)は紙面手前側に向いています。
4番目の置換基が上に位置するようにFischer投影式を書いたとき、1、2、3が時計回りに位置しているとR体、反時計回りに位置しているとS体と判別できます。
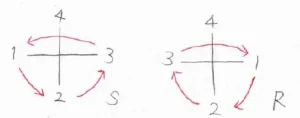
Fischer投影式を書いてR体かS体か判別できないときには、上記の形になるまで数字を入れ替えてください。
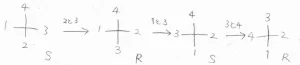
Fischer投影式には、2つの置換基を1回入れ替えるごとに絶対配置が反転するという性質があるので、R体かS体と判別できる形になるまでに数字を入れ替えた回数が偶数か奇数かで、もとの絶対配置も判別できます。
練習問題
それではここで、練習問題をやってみましょう。
次の3つのキラルな分子は、R体とS体のどちらになるかを判別してください。
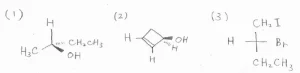
(1)与えられている2-ブタノールの構造をFischer投影式で表すと、こちらのようになります。
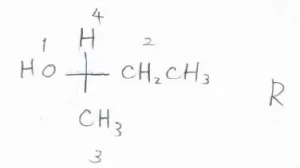
不斉炭素に直接結合している原子の中では、酸素がもっとも原子番号が大きいので、ヒドロキシ基が1番となります。
エチル基とメチル基ではエチル基のほうが優先されるので、エチル基が2番、メチル基が3番、残った水素が4番となります。
4が上にある形で、1、2、3と数えたとき、時計回りになるので、この2-ブタノールはR体だとわかります。
(2)まず、問題の3-ヒドロキシシクロブテンについて、水素が上にくるようにFischer投影式を書きます。
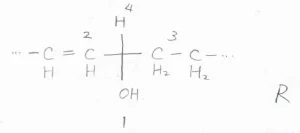
二重結合があるほうが優先されるので、優先順位はこのようになります。
1、2、3は時計回りに位置しているので、これもR体だとわかります。
(3)2-ブロモ-1-ヨードブタンについては、始めからFischer投影式が与えられています。
水素原子が上にないので、ヨードメチル基と交換したのが、下の形です。
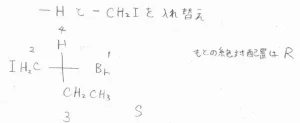
ヨードメチル基はエチル基よりも優先されます。
1、2、3は反時計回りに位置しているので、この絶対配置はSとなります。
ただし、置換基を奇数回入れ替えているので、元の構造は、これを反転したものになります。
したがって、元の絶対配置はRです。
まとめ
今回の内容は以上です。次回の有機化学の動画では、ハロゲン化されたアルカンで起こる求核置換反応という反応について、お話ししていきます。
間違いの指摘、リクエスト、質問等あれば、X(https://X.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




