こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Lennard-Jones 1、Lennard-Jones 2)
それでは内容に入っていきます!
レナード-ジョーンズポテンシャルとは?
始めに紹介しておくと、分子間相互作用のポテンシャル\(V\)が\(\displaystyle 4\varepsilon[(\frac{r_0}{r})^{12}-(\frac{r_0}{r})^6]\)で与えられるというものです。
\(\varepsilon\)と\(r_0\)は定数で、\(r\)は分子間距離を指します。
\(12\)乗の項が斥力項、\(6\)乗の項が引力項を表します。
引力相互作用ポテンシャルの分子間距離依存性
分子間ではたらく引力には、さまざまな種類があります。
それぞれの場合について、ポテンシャルの分子間距離依存性を見ていきましょう。
部分電荷間
まず、最も簡単なのは部分電荷間、つまりイオン同士ではたらく相互作用です。
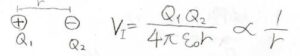
これは単純にクーロンの法則に従うため、ポテンシャルは\(r\)に反比例します。
部分電荷-永久双極子
そして、次のパターンは、イオンと永久双極子の相互作用です。
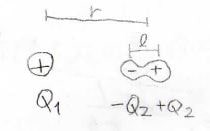
イオンの電荷を\(Q_1\)、永久双極子の正電荷を\(+Q_2\)、負電荷を\(-Q_2\)、双極子の長さを\(l\)とすると、ポテンシャルは下のように書けます。
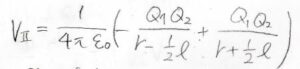
ここで、\(\displaystyle x=\frac{l}{2r}\)と置き、さらに\(l\)は\(r\)に比べて十分短いものとして近似をします。
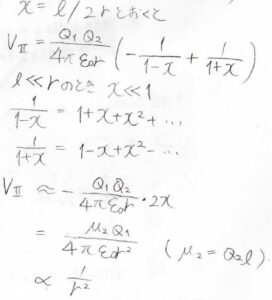
すると、\(x^2\)の項が残ってくるため、\(V\)は\(\displaystyle \frac{1}{r^2}\)に比例することになります。
ここで、\(Q_2l\)は双極子モーメントの大きさ\(\mu_2\)と書き換えています。
永久双極子-永久双極子
続いてのパターンは、永久双極子同士の相互作用です。
同一直線上に並んだ場合
まず、2つの双極子が同一直線上に並んでいたときについて考えると、ポテンシャルはこのように書けます。
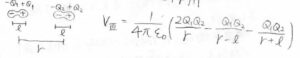
\(\displaystyle x=\frac{l}{r}\)として、先ほどと同様の近似をすると、\(V\)は\(\displaystyle \frac{1}{r^3}\)に比例するということが導かれます。
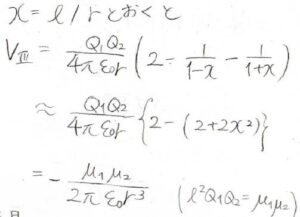
同一直線上に並んでいない場合
双極子が同一直線上にない場合には、下図のように角度\(\theta\)を定義すると、\(\displaystyle V=\frac{\mu_1\mu_2}{4\pi \varepsilon_0r^3}f(\theta)\)となります。
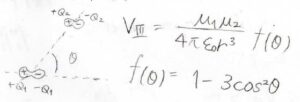
そして、\(f(\theta)\)は\(1-3\cos^2{(\theta)}\)で与えられます。
これは、双極子が自由に回転しない結晶に対応しています。
ランダムに回転する場合
流体、すなわち液体と気体の場合では、\(\theta\)がランダムに時間変化するので、\(V\)も平均化して考えなければいけません。
そこで、\(f(\theta)\)の球平均を計算すると、答えが\(0\)になります。
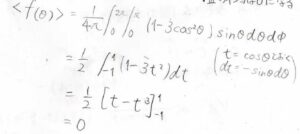
したがって、完全にランダムな回転が起こる流体中では、双極子同士の相互作用は平均化されてなくなるということがわかります。
熱運動による加重平均をとる場合
厄介なのはここからで、実際の流体中では、完全にランダムな回転にならない場合があります。
\(\theta=0\)のときは、他の値のときに比べて少し安定になるため、ここに重みをつけて平均化する必要があります。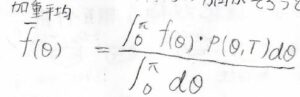
平均化するときの考え方はいくつかあるのですが、ここでは相互作用のポテンシャルと熱運動のエネルギーの大小関係に注目してみましょう。
これは、温度が高いときには熱運動が激しいので、ランダムな回転に近く、低温になるに従って\(\theta=0\)の寄与が大きくなるという考え方です。
このときの\(\theta\)の分布を表す\(p(\theta, T)\)は、ボルツマン分布に従うこととします。
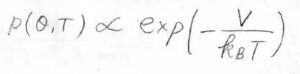
さらに、温度が十分に高く、双極子-双極子相互作用のポテンシャル\(V\)が\(k_\rm{B}\)\(T\)より十分に小さい場合は、\(\displaystyle \exp{(-\frac{V}{k_\rm{B}\mathit{T}})}\approx \displaystyle 1-\frac{V}{k_\rm{B}\mathit{T}}\)と近似できます。
すると、加重平均\(\bar{f(\theta)}\)はこのようにかけます。
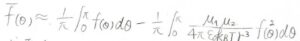
したがって、極座標における角度\(\varphi\)についても平均をとった球平均は、このようになります。

ここで\(\langle \rangle_0\)は完全にランダムな回転をしているときの球平均を意味します。
さっき計算したように第一項は\(0\)となりますが、第二項にある\(f(\theta)^2\)の球平均は\(\displaystyle \frac{2}{3}\)となります。
したがって、双極子同士の相互作用のポテンシャルは下のように書けて、\(\displaystyle \frac{1}{r^6}\)に比例することになります。
永久多極子-永久多極子
双極子でなくて、多極子であった場合には、\(r\)の次数も変わってきます。
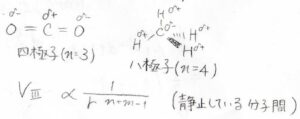
分子に存在する双極子モーメントの本数を\(n\)、\(m\)とすると、結晶におけるポテンシャルは\(\displaystyle \frac{1}{r^{n+m-1}}\)に比例します。
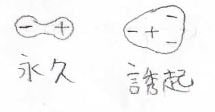
永久双極子-誘起双極子
続いて、永久双極子と誘起双極子の相互作用について考えてみましょう。
分極がない分子でも、永久双極子が近づいてくることで、電子の偏りが生じます。
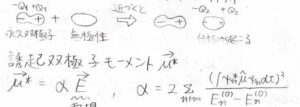
このようにしてできた双極子のことを誘起双極子と言います。
誘起双極子のモーメントの大きさは、永久双極子が作り出す電場の大きさに比例します。
その比例定数\(\alpha\)の単位は\(\rm{C^2\ J^{-1}\ m^{-1}}\)となるのですが、\(4\pi \varepsilon_0\)で割って、体積のパラメータとして表すこともあります。
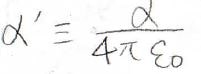
この量を分極率体積といい、ここでは\(\alpha’\)と表すことにします。
そして、永久双極子がつくる電場は、双極子モーメントと下のような関係になっており、電場の大きさは\(\displaystyle \frac{1}{r^3}\)に比例して減衰していきます。
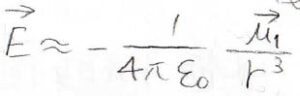
以上のことより、永久双極子-誘起双極子相互作用のポテンシャルはこのように書けます。
\(\displaystyle \frac{1}{r^6}\)に比例するのは、双極子-双極子相互作用で\(\displaystyle \frac{1}{r^3}\)に比例し、さらに誘起双極子モーメントの大きさも\(\displaystyle \frac{1}{r^3}\)に比例するからです。
ここで重要なことは、永久双極子から見たときに誘起双極子は自由に回転できないということです。
これは、永久双極子が近づいてきた方向に合わせて分極するためです。
したがって、ポテンシャルの球平均は温度に依存しません。
誘起双極子-誘起双極子
続いて、誘起双極子同士の相互作用を考えてみましょう。
永久双極子がなくても、ある時刻について着目すると、電子が偏在することがあります。
すると、それに伴って周りの分子も誘起されて双極子となります。
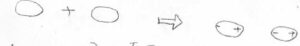
無極性であるはずの二原子分子でも、液体の状態をとることには、この相互作用が密接に関係しています。
この相互作用は分散相互作用、ロンドン相互作用とも呼ばれています。
相互作用のポテンシャルは、こちらのロンドンの式で書けます。

ここで、\(I\)は分子のイオン化エネルギーです。
相互作用する2つの分子のうち、一方が双極子になった時点であとは永久双極子と誘起双極子の相互作用と基本的に変わらないため、ポテンシャルは\(\displaystyle \frac{1}{r^6}\)に比例します。
引力相互作用のまとめ
ここまでのことをまとめると、熱運動を考慮して加重平均をとった双極子-双極子相互作用と永久双極子-誘起双極子相互作用、そして誘起双極子-誘起双極子相互作用の3つはすべてポテンシャルが\(\displaystyle \frac{1}{r^6}\)に比例することになります。
したがって、これらすべてをまとめると、\(C\)を正の定数として\(\displaystyle V=-\frac{C}{r^6}\)と表すことができます。
ただし、ここで注意したいのは、この表現が引力相互作用を完全に表したものではないということです。
まず、回転が起こらない結晶や、イオンが存在する系では成り立ちません。
また、水素結合はもっと大きな距離依存性をもちます。
溶媒との親和性に起因する疎水性相互作用も例外です。
そして、誘起されたときに必ずしも双極子になるとは限らないため、厳密には誘起多極子の寄与を考えなければいけませんが、ここでは無視しています。
3分子間ではたらく引力相互作用
そして、ここまでは2つの分子間で引力を考えていましたが、より一般的に3つの分子についても考えてきます。
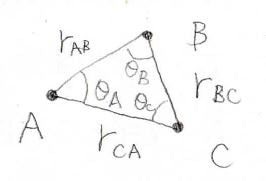
すると、3点が同一直線上に並んでいるときが熱力学的に最も安定となり、正三角形を作るときに最も不安定になります。

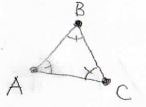
これを式で表したのが、こちらのアクシルロッド-テラーの式であり、これは引力相互作用の非加成性を示すものとなっています。
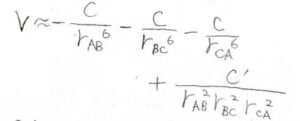
![]()
ここで、\(\displaystyle a\approx \frac{3}{4}\alpha’C\)です。
したがって、引力のポテンシャルが\(\displaystyle \frac{1}{r^6}\)に比例するという考え方では、3つ以上の点の位置関係による効果も考えられておらず、あくまで2つの分子間距離だけに着目した大雑把なものだと言えます。
斥力相互作用
次に、斥力相互作用を考えていきます。
最も簡単なのは、剛体球モデルです。
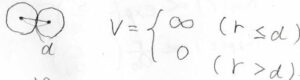
分子は球であるとして、中心同士が直径まで近づいたときにポテンシャルが発散します。
直径よりも離れているときには、\(V=0\)です。
とても簡単なモデルですが、これでもコロイド粒子の挙動や排除体積効果などを説明することができる有用なものです。
ただし、不連続な関数なので、例えば微分して力の大きさを求めたいときなどには、使えません。
ミーポテンシャル
そこで、引力相互作用があっても短距離側で+側へ発散するような関数として、斥力のポテンシャルを導入したのが、こちらのミーポテンシャルです。
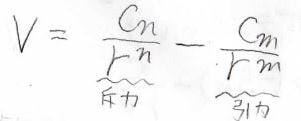
これは一般式で、\(C_n\)、\(C_m\)はいずれも正の定数、そして\(n\)は\(m\)より大きいです。
そして、特に\(n=12\)、\(m=6\)のポテンシャルのことをレナード-ジョーンズポテンシャル、もしくは(6,12)ポテンシャルと言います。
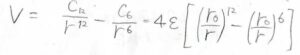
中には、上記のミーポテンシャルを広義のレナード-ジョーンズポテンシャルとして紹介しているものもあります。
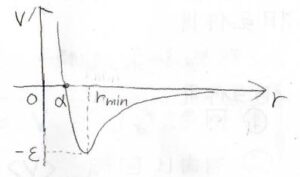
グラフで示したものがこちらで、赤が斥力、青が引力、黒がその和を示しています。
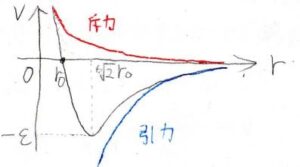
2つの定数\(\varepsilon\)と\(r_0\)は、レナード-ジョーンズパラメータと呼ばれ、それぞれは井戸の深さと\(V=0と\)なる分子間距離を示しています。
これを使うと、主に試料の表面の様子を観察する目的で用いられる原子間力顕微鏡、略してAFMで観測される力の大きさは、ポテンシャルの負の勾配として、このように計算されます。

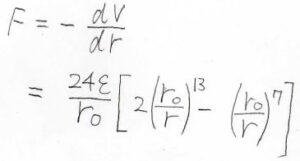
バッキンガムポテンシャル
しかし厳密には、斥力項として\(\displaystyle \frac{1}{r^{12}}\)に比例するという表現は、かなり大雑把です。
電子間反発が軌道の重なりによって起こると考えた場合、動径関数の式から\(\exp{(-r)}\)に比例するというほうが信頼できます。

実際に斥力項を指数関数でおいたポテンシャルは、バッキンガムポテンシャル、もしくはexp-6ポテンシャルと言います。
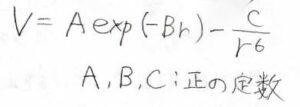
実在気体のファンデルワールスパラメータを考える際には、レナード-ジョーンズポテンシャルではなく、こちらの式が使われました。
しかし、こちらのポテンシャルも問題があって、短距離側だと指数部分が\(1\)に収束するので、引力優性となってしまいます。

もちろん、これは現実的ではありません。
そこで、こちらの修正バッキンガムポテンシャルというものもあります。
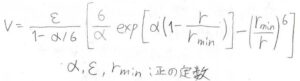
ただ、ここまでくるとパラメータが3つも出てくる上に、式の形も複雑です。
そもそも、引力項が\(\displaystyle \frac{1}{r^6}\)に比例するというのも大雑把な近似でしたので、そこまでの厳密さを求めない場合は、むしろパラメータが2つのレナード-ジョーンズポテンシャルのほうが使い勝手がよいことも多いです。
そのため、いまでも分子動力学シミュレーションでは、レナード-ジョーンズポテンシャルのほうがよく見かける式となっています。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!





