こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Maxwell relations)
それでは内容に入っていきます!
熱力学基本式
まずは、熱力学基本式の話から入っていきます。
熱力学第一法則より内部エネルギーの微小変化\(\rm{d}\)\(U\)は、系へ与えられた微小な熱量\(\rm{d’}\)\(q\)と系へなされた微小な仕事\(\rm{d’}\)\(w\)との和で表されます。
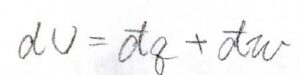
ここで、系が均一な組成をもつ閉鎖系であったとき、つまり外界と熱のやりとりだけして、物質のやりとりをしない場合は、可逆変化で\(\rm{d’}\)\(q=T\rm{d}\)\(S\)となります。
ここで\(T\)は絶対温度、\(S\)はエントロピーです。
さらに、非膨張の仕事がなかった場合は\(\rm{d’}\)\(w=-p\rm{d}\)\(V\)が成立します。
以上のことをまとめると、均一な組成をもつ閉鎖系で、非膨張の仕事を伴わない可逆変化が起こったとき、内部エネルギーの変化\(\rm{d}\)\(U\)は\(T\rm{d}\)\(S-p\rm{d}\)\(V\)と表されます。
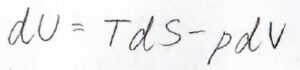
この式のことを熱力学基本式といいます。
内部エネルギーは状態関数であり、その変化量は経路に依存しないはずなので、この等式はその変化の可逆・不可逆に関わらず成り立つことになります。
不可逆なときには、\(\rm{d’}\)\(q\)は\(T\rm{d}\)\(S\)より小さく、\(\rm{d’}\)\(w\)は\(-p\rm{d}\)\(V\)より大きくなるわけですが、もともと均一で組成の変化もない限り、その和は常に\(T\rm{d}\)\(S-p\rm{d}\)\(V\)になるということです。
内部エネルギーから導かれるマクスウェルの関係式
熱力学基本式は\(S\)と\(V\)を変数とした二変数関数\(U\)の全微分と見ることができます。
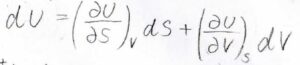
そうすると、\(\displaystyle (\frac{\partial U}{\partial S})_V=T\)、\(\displaystyle (\frac{\partial U}{\partial p})_S=-p\)だということがわかります。
そして、数学的に常に成立するわけではありませんが、状態関数である内部エネルギーについては、偏微分の順序交換が可能です。
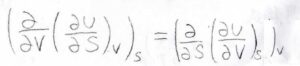
つまり、内部エネルギーをエントロピーについて偏微分してから体積について偏微分した値は、内部エネルギーを体積について偏微分してからエントロピーについて偏微分した値と一致します。
このことより、エントロピー一定として温度を体積について偏微分した値は、体積一定として圧力をエントロピーについて偏微分した値に\(-1\)をかけた値に等しくなります。

この関係式を、マクスウェルの関係式といいます。
この式を使えば、実験的に測定が難しい量も測定することができます。
圧力のエントロピー依存性が測れなくても、温度の体積依存性だったら簡単に測れるので、そこから計算が可能です。
化学熱力学の基本式とマクスウェルの関係式
それで、熱力学基本式とマクスウェルの関係式は、エンタルピーやヘルムホルツエネルギー、ギブズエネルギーに関しても同様のものを導くことができます。
エンタルピーについて
例えば、\(H=U+pV\)で定義されるエンタルピーの場合、\(\rm{d}\)\(H=T\rm{d}\)\(S-p\rm{d}\)\(V+\rm{d}\)\((pV)\)となります。
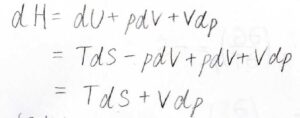
\(\rm{d}\)\((pV)=p\rm{d}\)\(V+V\rm{d}\)\(p\)より、\(\rm{d}\)\(H=T\rm{d}\)\(S+V\rm{d}\)\(p\)という基本式が導かれます。
エンタルピーをエントロピーと圧力の二変数関数とみなせば、\(\displaystyle (\frac{\partial H}{\partial S})_p=T\)、\(\displaystyle (\frac{\partial H}{\partial p})_S=V\)という式が得られます。
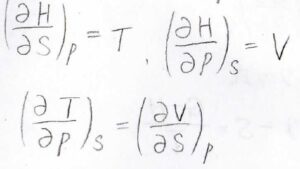
最後に偏微分の順序交換が可能であることを利用して、\(\displaystyle (\frac{\partial T}{\partial p})_S=(\frac{\partial V}{\partial S})_p\)というマクスウェルの関係式が導かれます。
ヘルムホルツエネルギーについて
\(A=U-TS\)で定義されるヘルムホルツエネルギーに関しては、\(\rm{d}\)\(A=T\rm{d}\)\(S-p\rm{d}\)\(V-T\rm{d}\)\(S-S\rm{d}\)\(T\)となります。

その結果、\(T\rm{d}\)\(S\)がキャンセルして、\(\rm{d}\)\(A=-p\rm{d}\)\(V-S\rm{d}\)\(T\)という基本式が導かれます。
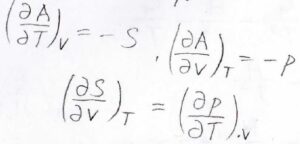
ヘルムホルツエネルギーを体積と温度の二変数とすると、偏微分の順序交換により、\(\displaystyle (\frac{\partial S}{\partial V})_T=(\frac{\partial p}{\partial T})_V\)というマクスウェルの関係式も出てきます。
ギブズエネルギーについて
最後、\(G=H-TS\)で定義されるギブズエネルギーに関しては、\(\rm{d}\)\(G=V\rm{d}\)\(p-S\rm{d}\)\(T\)となります。

ギブズエネルギーを温度と圧力の二変数関数とすると、\(\displaystyle (\frac{\partial V}{\partial T})_p=-(\frac{\partial S}{\partial p})_T\)というマクスウェルの関係式が導かれます。
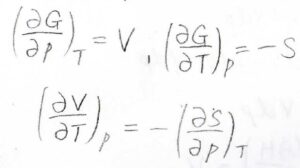
ギブズ-ヘルムホルツの式
また、ギブズエネルギーの定義が\(G=H-TS\)であることから、\(\displaystyle -S=\frac{G-H}{T}\)と書けます。
したがって、\(\displaystyle -S=(\frac{\partial G}{\partial T})_p=\frac{G}{T}-\frac{H}{T}\)です。
この結果を利用して、圧力一定で\(\displaystyle \frac{G}{T}\)を温度について偏微分すると、その値は\(\displaystyle -\frac{H}{T^2}\)となります。
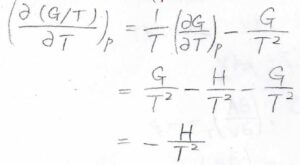

この式はギブズ-ヘルムホルツの式と呼ばれていて、エンタルピーの値からギブズエネルギーの温度依存性がわかるということを表しています。
任意の変化に伴うギブズエネルギー変化を\(\Delta G\)、エンタルピー変化を\(\Delta H\)とすると、\(\displaystyle [\frac{\partial (\Delta G/T)}{\partial T}]_p=-\frac{\Delta H}{T^2}\)となります。
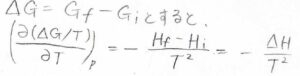
この関係は、平衡定数や電池の起電力の温度依存性を反応熱から予想することに使うことができます。
また、熱量計による反応熱の測定が困難な場合には、平衡定数や起電力の温度依存性から反応熱を見積もることにも利用できます。
練習問題
それでは最後に練習問題をやって終わります。
(1)内部エネルギー\(U\)を温度と体積の二変数関数としてみなしたときに出てきた内圧\(\pi_T\)が\(\displaystyle T(\frac{\partial p}{\partial T})_V-p\)と表せることを示してください。
(2)エンタルピー\(H\)を温度と圧力の二変数関数としてみなしたときに出てくる等温ジュール-トムソン係数\(\mu_T\)を温度、圧力、体積だけを使って表すとどうなるでしょうか?
これと、熱力学基本式を合わせると、\(\displaystyle \pi_T=T(\frac{\partial S}{\partial V})_p-p\)となります。

ここで、ヘルムホルツエネルギーについての基本式から導かれたマクスウェルの関係式を使います。
すると、\(\displaystyle (\frac{\partial S}{\partial V})_p=(\frac{\partial p}{\partial T})_V\)より\(\displaystyle \pi_T=T(\frac{\partial p}{\partial T})_V-p\)という式が導かれます。
(2)もまったく同じ手順で解けます。
等温ジュール-トムソン係数\(\displaystyle \mu_T=(\frac{\partial H}{\partial p})_T\)で、\(\rm{d}\)\(H=T\rm{d}\)\(S+V\rm{d}\)\(p\)であるため、\(\displaystyle \mu_T=T(\frac{\partial S}{\partial p})_T+V\)となります。
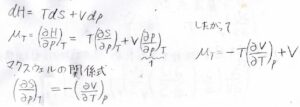
そして、ギブズエネルギーについての基本式から得られたマクスウェルの基本式\(\displaystyle (\frac{\partial S}{\partial p})_T=-(\frac{\partial V}{\partial T})_p\)より、\(\displaystyle \mu_T=-T(\frac{\partial V}{\partial T})_p+V\)となります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!