こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(virial)
それでは、内容に入っていきます!
理想気体と実在気体の違い
それではまず、改めて理想気体と実在気体の違いを整理してみましょう。
高校で習った通り、理想気体の状態方程式は\(pV=nRT\)ですが、この式では2つの要素が無視されています。
それは、分子の大きさとファンデルワールス力に代表される分子間力です。
それらをモデル化して考慮したのがファンデルワールスの状態方程式です。
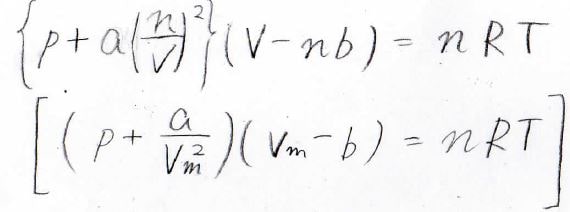
ここで、\(a\)と\(b\)はファンデルワールスパラメータと呼ばれ、物質定数になります。
詳しくはこちらを参照してください。

\(a\)は分子間力の大きさの度合いを表しており、\((n/V)^2\)の部分は、2つの分子が衝突する確率を考えています。
\(b\)は分子の中心同士がこれ以上近づけなくなる領域の体積であり、排除体積と呼ばれます。
今は分子\(1\ \rm{mol}\)あたりの量になっています。
下側の式は、上側の式の両辺を物質量\(n\)で割った形になります。
そして、理想気体と実在気体の状態方程式では1つ明確な違いがあって、それが今回のテーマになります。
それは、\(pV_\rm{m}\)\(\)と\(RT\)の比です。
理想気体では\(1\)になりますが、実在気体では\(1\)にならないので、この比を実在気体の非理想性を表すパラメータとして考えます。
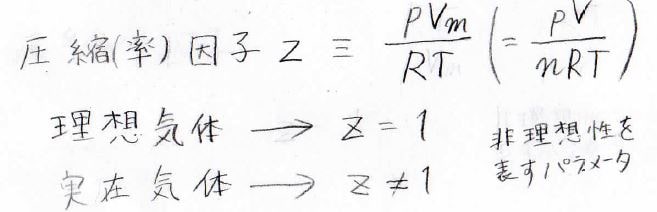
この比は、圧縮因子、または圧縮率因子、圧縮係数と呼ばれ、\(z\)で書かれることが多いです。
任意の実在気体の圧縮因子を表す場合には、テイラー展開などの要領で級数を使うというアプローチを考えることができます。
実在気体も高温低圧条件下では理想気体に近づくため、\(p\rightarrow 0\)で\(z\rightarrow 1\)になるような関数を作ることにします。
実際にべき級数として\(z\)を表したのが、こちらの式になります。
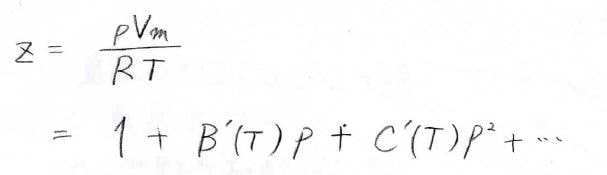
理想気体では、ボイルの法則より、\(p\)が\(V_\rm{m}\)\(\)に反比例するため、この式は下のように書き換えることもできます。
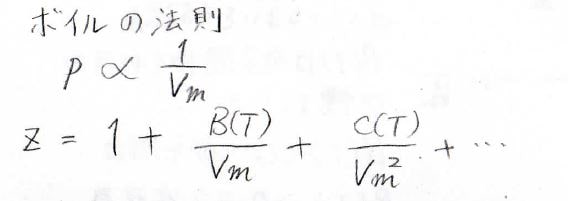
ここで、\(B(T)\)と\(C(T)\)はそれぞれ第2ビリアル係数、第3ビリアル係数と呼ばれ、温度に依存する、物質に固有の関数になります。
ちなみに、第1ビリアル係数は\(1\)になります。
この式の両辺に\(RT\)をかけ式をビリアル状態方程式といいます。
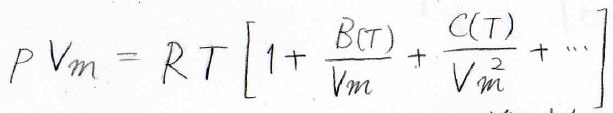
\(B(T)\)の物理的な意味
ここで、第2ビリアル係数\(B(T)\)がもつ物理的な意味について、もう少し考えてみましょう。
モル体積\(V_\rm{m}\)\(\)が大きいときには、多くの物質で\(C(T)/V_\rm{m}\)\(\)は\(B(T)\)よりも十分に小さいと考えることができるため、\(z\)を\(V_\rm{m}\)\(^{-1}\)で偏微分した値は、\(B(T)\)と近似できます。
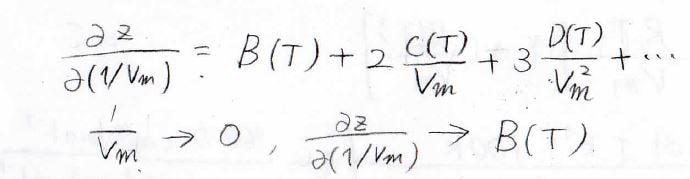
グラフの縦軸に\(z\)、横軸に\(V_\rm{m}\)\(^{-1}\)をとると、\(V_\rm{m}\)\(^{-1}\)を小さくしていったときの\(z\)の傾きが\(B(T)\)になります。

そして、\(B(T)\)は温度の関数であるため、温度を変えていくと、\(z\)は以下のように変化します。
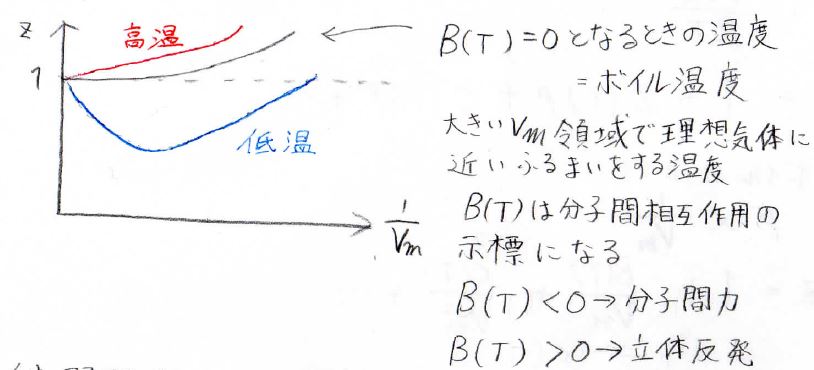
ここで青が低温、赤が高温になります。
ある温度で\(B(T)=0\)となり、そのときの温度をボイル温度と呼びます。
この温度では、広いモル体積の範囲で理想気体に近い挙動を示すということになります。
そして、\(B(T)\)の値は、分子間で立体反発と分子間力のどちらが優勢なのかを示す指標となります。
低温で\(B(T)\)が負になるのは分子間力が優勢であることに対応します。
反対に、高温で\(B(T)\)が正になるのは、膨張した排除体積の影響が優勢になるということに対応します。
練習問題
それでは最後、練習問題をやってみましょう。
体積\(1\ \rm{L}\)の容器の中に窒素ガスが\(0.4\ \rm{mol}\)あったとき、\(100\ \rm{K}\)における圧力はいくらでしょうかというのが問題です。
ただし、圧縮因子は二次の項までで記述されて、その第2ビリアル係数は\(-160.0\ \rm{cm^3\ mol^{-1}}\)であるとします。
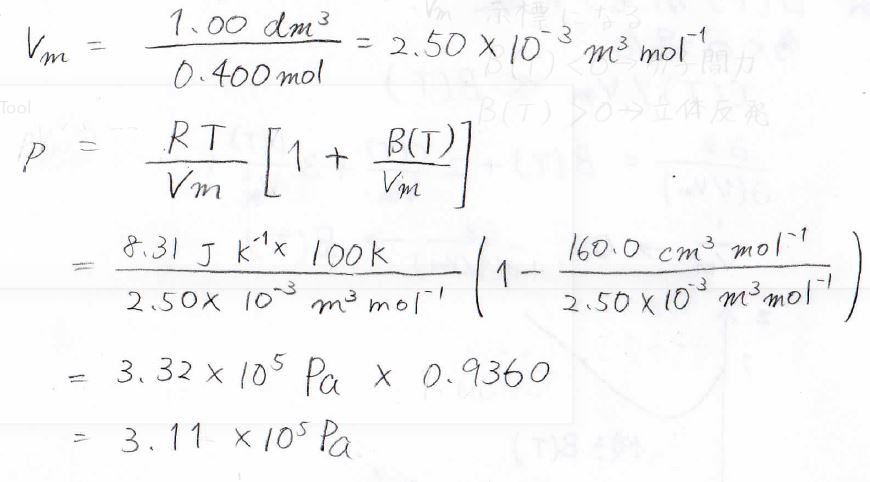
求めるべき圧力\(p\)は、二次まででこのように書けるため、あとはこれを計算することで、\(3.11\times 10^5\ \rm{Pa}\)と出てきます。
まとめ
はい、それでは今回の内容は以上なので、最後軽くおさらいをやって終わります。
今回は、圧縮率因子とビリアル状態方程式を使って、実在気体の非理想性を考えました。
圧縮率因子は\(pV_\rm{m}\)\(/RT\)で定義され、\(z\)で表されます。\(z\)が1の時には理想気体、\(z\)が\(1\)から外れるほど、非理想的であることになります。
一般的に\(z\)を表すときには、べき級数を使うことができ、そうやって作った状態方程式をビリアル状態方程式と呼びます。
第2ビリアル係数は分子間で引力と斥力のどちらが優勢なのかの指標になり、ちょうど\(0\)になるときの温度はボイル温度と呼ばれます。
それではどうも、ありがとうございました!