こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(contribution to mean energy and entropy)
※シートの後半は、次回の記事の内容です。

平均エネルギーと分子分配関数の関係
始めに、分子分配関数から分子の平均エネルギーが求められることを確かめます。
過去の記事で、集合分配関数を使って、内部エネルギーを表した方法とほとんど同じです。
詳しくは、こちらを参照してください。

まず、基底状態を基準にとったエネルギー準位を\(\varepsilon_i\)とします。
ボルツマン分布に従う分子の平均エネルギー\(\langle \varepsilon\rangle\)は、全エネルギー\(E\)を分子数\(N\)で割ったものであり、占有数の比から期待値をとると、\(\displaystyle \frac{1}{q}\sum_{i}\varepsilon_i\exp{(-\beta \varepsilon_i)}\)と書けます。
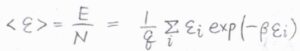
ここで、\(q\)は分子分配関数、\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)、\(k_\rm{B}\)はボルツマン定数、\(T\)は絶対温度です。
\(\displaystyle \varepsilon_i\exp{(-\beta \varepsilon_i)}=-[\frac{\partial}{\partial\beta}\exp{(-\beta \varepsilon_i)}]_V\)であることから、\(\displaystyle \langle \varepsilon\rangle=-\frac{1}{q}(\frac{\partial q}{\partial \beta})_V\)となります。
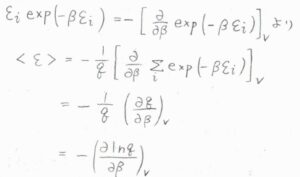
ここで、偏微分の形にしているのは、エネルギー準位が\(\beta\)以外の変数をもつためです。
系の体積が変化すると、並進のエネルギー準位が変化するため、体積を一定に保ったまま、\(\beta\)で微分する必要があります。
さらに、\(\displaystyle \frac{1}{q}=\frac{\rm{d}\ln{\mathit{q}}}{\rm{d}\mathit{q}}\)より、\(\displaystyle \langle \varepsilon\rangle=-(\frac{\partial \ln{q}}{\partial \beta})_V\)と書けます。
ただし、ここで注意したいことは、このようにして求められた平均エネルギーは基底状態のエネルギーを基準にとったものなので、絶対零度近傍では、必ず\(0\)に収束します。
完全に静止している状態を基準にとった場合の平均エネルギーは、これに基底状態のエネルギーを足した値になります。
それでは、前回考えた分子分配関数の寄与を利用して、それぞれの自由度に割り当てられるエネルギーの平均値を求めていきましょう。
こちらの記事と合わせて、ご覧ください。

平均電子エネルギー
始めに、電子の平均エネルギーを求めます。
分子分配関数を考えたときと同様ですが、多くの分子において、基底状態からの電子励起に必要なエネルギーは、並進や回転、振動に比べてきわめて大きいため、ほとんどの分子は電子基底状態にあると考えられます。
そのため、基底状態のエネルギーを基準にとった平均エネルギー\(\langle \varepsilon^\rm{E}\rangle\)は、\(0\)となります。
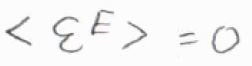
ただし、スピン-軌道カップリングなどにより、小さな励起エネルギーをもつ分子では、第一励起状態も考慮する必要があります。
前回も紹介した一酸化窒素については、励起エネルギーを\(\varepsilon\)として、電子分配関数は\(2+2\exp{(-\beta \varepsilon)}\)で与えられます。
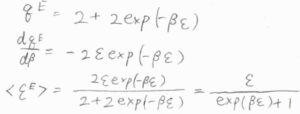
\(\displaystyle \frac{\rm{d}\mathit{q}^\rm{E}}{\rm{d}\beta}=-2\varepsilon\exp{(-\beta\varepsilon)}\)となるので、\(\langle \varepsilon^\rm{E}\)\(\displaystyle \rangle=-\frac{1}{q^\rm{E}}\frac{\rm{d}\mathit{q}^\rm{E}}{\rm{d}\beta}\)に代入して、\(\langle \varepsilon^\rm{E}\)\(\displaystyle \rangle=\frac{\varepsilon}{\exp{(\beta\varepsilon)}+1}\)と求められます。
絶対零度近傍では、\(\exp{(\beta\varepsilon)}\)が無限大に発散するので、\(\langle \varepsilon^\rm{E}\rangle\)\(=0\)となります。
平均スピンエネルギー
ここで、前回も話したスピン状態についても、少しお話ししておきます。
外部磁場\(\boldsymbol{B}\)のもとで、2つのスピン状態に分裂した電子の平均エネルギーを考えます。
まず、スピン分配関数\(q^\rm{S}\)は、\(1+\exp{(-2\beta \mu_\rm{B}\mathit{B})}\)で与えられます。
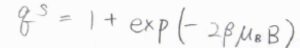
ここで、\(\mu_\rm{B}\)はボーア磁子、\(B\)は外部磁場の大きさで、電子の\(g\)因子を\(2\)として考えています。
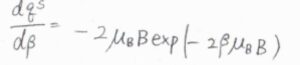
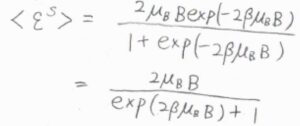
\(\displaystyle \frac{\rm{d}\mathit{q}^\rm{S}}{\rm{d}\beta}=-2\mu_\rm{B}\)\(B\exp{(-2\beta\mu_\rm{B}\mathit{B})}\)となることから、\(\langle \varepsilon^\rm{S}\)\(\displaystyle \rangle=\frac{2\mu_\rm{B}\mathit{B}}{\exp{(2\beta\mu_\rm{B}\mathit{B})}+1}\)と求められます。
平均並進エネルギー
続いて、並進の平均エネルギーを求めます。
まず、ある程度温度が高く、体積が大きい系において、三次元の並進分配関数\(q^\rm{T}\)は、\(\displaystyle \frac{V}{\Lambda^3}\)で与えられます。
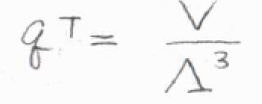
ここで、\(\Lambda\)は熱波長、もしくは熱的ド・ブロイ波長という長さの次元をもつパラメータで、\(\displaystyle (\frac{\beta}{2\pi m})^\frac{1}{2}\)と定義されます。
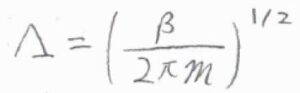
\(m\)は分子の質量です。
これをもとに、平均の並進エネルギーを求めると、\(\langle \varepsilon^\rm{T}\rangle\)\(\displaystyle =\frac{3}{2\beta}\)となります。
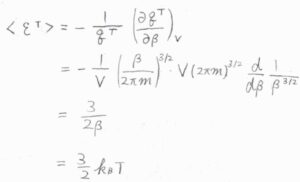
\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)を代入すると、\(\displaystyle \frac{3}{2}k_\rm{B}\)\(T\)となります。
1次元で考えれば、\(q^\rm{T}\)\(\displaystyle =\frac{1}{2}k_\rm{B}\)\(T\)であり、3つの自由度に\(\displaystyle \frac{1}{2}k_\rm{B}\)\(T\)ずつエネルギーが割り当てられるという等分配則と一致した結果が得られます。
平均回転エネルギー
次に、回転の平均エネルギーを求めます。
分子の形状によって、回転に割り当てられる自由度は変化するので、ここでは直線型回転子について考えることにします。
主軸に垂直で、互いに垂直な2つの軸についての回転運動に自由度が割り当てられるので、自由度は\(2\)になります。
したがって、等分配則より高温域における平均の回転エネルギーは、\(k_\rm{B}\)\(T\)になると予想されます。
対称数があると複雑になるので、ここでは非対称な分子で考えることにします。
回転分配関数\(q^\rm{R}\)は、\(\displaystyle \sum_J (2J+1)\exp{[-\beta h c \tilde{B}J(J+1)]}\)で与えられます。
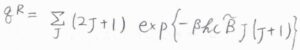
ここで、\(J\)は回転量子数、\(h\)はプランク定数、\(c\)は光の速さ、\(\tilde{B}\)は回転定数です。
分配関数を3つ目の項まで書き下すと、\(1+3\exp{(-2\beta h c \tilde{B})}+5\exp{(-6\beta h c \tilde{B})}\)になります。
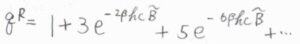
また、これらの項を\(\beta\)について微分すると、\(-6hc\tilde{B}\exp{(-2\beta h c \tilde{B})}-30hc\tilde{B}\exp{(-6\beta h c \tilde{B})}\)になるので、この結果を平均エネルギーの式に代入すると、
\(\langle \varepsilon^\rm{R}\)\(\displaystyle \rangle\approx \frac{6hc\tilde{B}e^{-2\beta h c \tilde{B}}+30hc\tilde{B}e^{-6\beta h c \tilde{B}}+84hc\tilde{B}e^{-12\beta h c \tilde{B}}}{1+3e^{-2\beta h c \tilde{B}}+5e^{-6\beta h c \tilde{B}}}hc\tilde{B}\)というかなり煩雑な式になることがわかります。
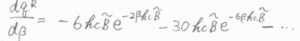
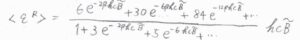
ただ、絶対温度\(T\)が回転特性温度\(\theta^\rm{R}\)よりも十分に高ければ、\(q^\rm{R}\)\(\displaystyle =\frac{1}{\beta hc\tilde{B}}\)と近似できるので、\(\langle \varepsilon^\rm{R}\)\(\displaystyle \rangle=\frac{1}{\beta}\)というとても簡単な答えになります。
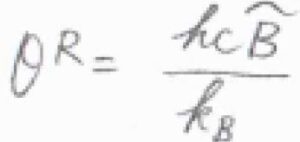
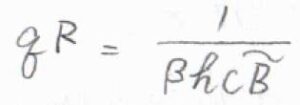
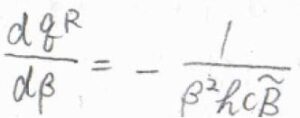
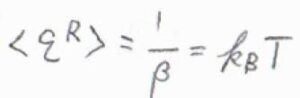
\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)より、\(\langle \varepsilon^\rm{R}\)\(\rangle=k_\rm{B}\)\(T\)となるので、この答えは等分配則からくる予想と一致します。
平均振動エネルギー
最後に、平均の振動エネルギーを求めます。
まず、一次元調和振動子についての振動分配関数\(q^\rm{V}\)は、\(\displaystyle \frac{1}{1-\exp{(-\beta \hbar \omega)}}\)です。
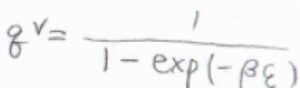
ここで、\(\displaystyle \hbar=\frac{h}{2\pi}\)、\(\omega\)は角周波数です。
これを\(\beta\)で微分すると、\(\displaystyle -\frac{\hbar \omega \exp{(-\beta \hbar \omega)}}{[1-\exp{(-\beta \hbar \omega)}]^2}\)となります。
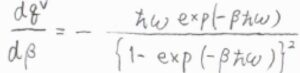
これらを平均エネルギーの式に代入すると、\(\langle \varepsilon^\rm{V}\)\(\displaystyle \rangle=\frac{\hbar \omega}{\exp{(\beta \hbar \omega)}-1}\)となります。
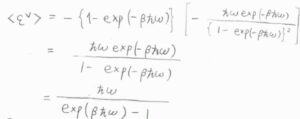
ただ、これは零点エネルギーを基準にとった値のため、完全に静止している状態のエネルギーを基準にすると、\(\langle \varepsilon^\rm{V}\)\(\displaystyle \rangle=\frac{\hbar \omega}{\exp{(\beta \hbar \omega)}-1}+\frac{1}{2}\hbar \omega\)となります。
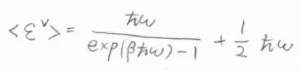
絶対温度\(T\)が振動特性温度\(\theta^\rm{V}\)より十分高いときには、指数関数のマクローリン展開より、\(\langle \varepsilon^\rm{V}\)\(\displaystyle \rangle=\frac{1}{\beta}+\frac{1}{2}\hbar \omega\)となります。
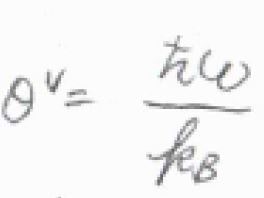
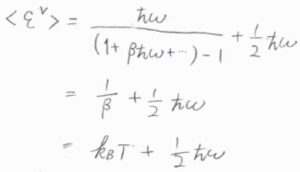
\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)を代入すると、\(\langle \varepsilon^\rm{V}\)\(\rangle=k_\rm{B}\)\(\displaystyle T+\frac{1}{2}\hbar \omega\)です。
振動の自由度は\(1\)なので、等分配則からくる予想と一致しないように思えるかもしれません。
しかし、一次元調和振動子のエネルギーは、運動エネルギー\(\displaystyle \frac{p_x^2}{2m}\)とポテンシャルエネルギー\(\displaystyle \frac{1}{2}kx^2\)の和であり、これら2つの2乗項それぞれに平均エネルギー\(\displaystyle \frac{1}{2}k_\rm{B}\)\(T\)が割り当てられることになります(\(p_x\)は運動量、\(k\)は力の定数)。
そのため、計算された\(\langle \varepsilon^\rm{V}\)\(\rangle\)は、等分配則と一致していると言えます。
分子が複数の基準振動モードをもっているときには、それぞれの振動モードについての平均エネルギーの和が、全体の平均エネルギーとなります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




