こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Laue condition)
それでは内容に入っていきます!
ラウエ関数
まず、これは前回も少し触れたことですが、結晶全体の構造因子\(F\)は、1つの単位胞について考えたうえで、さらに、それが繰り返されることも考慮されます。
前回の記事はこちらです。

反射光強度\(I\)は振幅の二乗に比例することから、\(\displaystyle I \propto |\sum_j \exp{(\rm{i}\mathit{\boldsymbol{q}\cdot \boldsymbol{r}_j})}|^2 \)となります。
ここで、\(j\)は単位胞につけたラベル番号です。
\(\boldsymbol{q}\)は散乱ベクトル、\(\boldsymbol{r}\)は位置ベクトルです。
さらに、単位胞の基本ベクトルを\(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{c}\)として、\( \boldsymbol{r}_j=x_j\boldsymbol{a}+y_j\boldsymbol{b}+z_j\boldsymbol{c} \)とすると、\(\displaystyle I\propto |\sum_{x=0}^{N_a-1}\exp{(\rm{i}\mathit{x\boldsymbol{q}\cdot \boldsymbol{a}})}|^2|\sum_{y=0}^{N_b-1}\exp{(\rm{i}\mathit{y\boldsymbol{q}\cdot \boldsymbol{b}})}|^2|\sum_{z=0}^{N_c-1}\exp{(\rm{i}\mathit{z\boldsymbol{q}\cdot \boldsymbol{c}})}|^2 \)と書けます。
ここで、\( N_a \)、\( N_b \)、\( N_c \)は、それぞれの基本ベクトル方向についての単位胞の個数です。
\(\displaystyle |\sum_{x=0}^{N_a-1}\exp{(\rm{i}\mathit{x\boldsymbol{q}\cdot \boldsymbol{a}})}|^2 \)だけを取り出してみると、これは初項が\(1\)で公比が\( \exp{(\rm{i}\mathit{\boldsymbol{q}\cdot \boldsymbol{a}})} \)の等比数列の和の二乗であるため、\(\displaystyle \frac{|1-\exp{(\rm{i}\mathit{N_a\boldsymbol{q}\cdot \boldsymbol{a}})}|^2}{|1-\exp{(\rm{i}\mathit{\boldsymbol{q}\cdot \boldsymbol{a}})}|^2} \)と表せます。
さらにオイラーの公式と2倍角の公式、半角の公式を使うと、\(\displaystyle \frac{\sin^2{(\frac{1}{2}N_a\boldsymbol{q}\cdot \boldsymbol{a})}}{\sin^2{(\frac{1}{2}\boldsymbol{q}\cdot \boldsymbol{a})}} \)となります。
\(\boldsymbol{b}\)や\(\boldsymbol{c}\)の方向についても同様に変形できるため、反射光強度\(I\)は、こちらの関数に比例することになります。
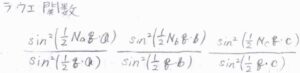
この関数のことをラウエ関数と言います。
縦軸に\(\boldsymbol{a}\)についての寄与、横軸に\(\displaystyle \frac{\boldsymbol{q}\cdot \boldsymbol{a}} {2\pi} \)をとると、横軸が整数となるときに大きなピークが周期的に現れる形になります。
\( N_a=3 \)のとき
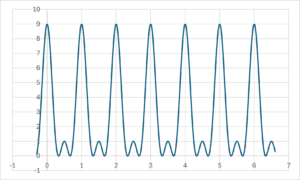
\( N_a=5 \)のとき
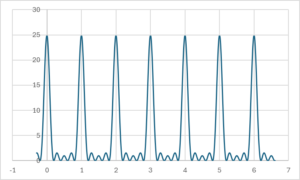
\( N_a=10 \)のとき
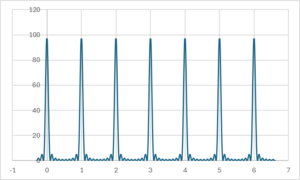
※それぞれのグラフで、縦軸の値が変化していることに注意してください。
主極大と呼ばれる大きなピークの高さは\( N_a^2 \)で与えられ、半値幅はおよそ\(\displaystyle \frac{1}{N_a} \)となります。
また、大きなピークの間には、副極大と呼ばれる小さなピークが現れます。
これらは\( N_a \)の増加に伴って、数は増えていきますが、その高さは低くなっていきます。
以上のことより、単位胞の構造が繰り返されるほど、よりくっきりとした回折図形が現れるということになります。
ラウエ条件(ラウエの式)
回折条件としては、グラフの横軸である\(\displaystyle \frac{\boldsymbol{q}\cdot \boldsymbol{a}}{2\pi} \)が整数であるということになるので、\(h\)を整数とすると、\( \boldsymbol{q}\cdot \boldsymbol{a}=2\pi h \)となります。
また、残りの2方向についても、\(k\)と\(l\)を整数として、\( \boldsymbol{q}\cdot \boldsymbol{b}=2\pi k \)、\( \boldsymbol{q}\cdot \boldsymbol{c}=2\pi l \)が条件になります。
これら3つの式をまとめてラウエ条件もしくはラウエの式と言います。
これを満たすようなベクトル\(\boldsymbol{G}\)と\(\boldsymbol{q}\)が一致するという形で簡単に書くこともあります。
整数である\(h\)、\(k\)、\(l\)はラウエ指数と呼ばれます。
ラウエ指数はミラー指数と似ていますが、あくまで数学的にラウエ関数が主極大となったときの反射指数を意味しており、指数どうしが\(1\)以外の公約数をもたないとするミラー指数のような制限はありません。
また、ラウエ指数は特定の面を指すものではないので、かっこを付けて表記することはありません。
逆格子ベクトル
そして、先ほど出てきたベクトル\(\boldsymbol{G}\)ですが、これは逆格子ベクトルというもので、ラウエ指数を使って\( h\boldsymbol{b}_1+k\boldsymbol{b}_2+l\boldsymbol{b}_3 \)と書けます。
ただし、\( \boldsymbol{a}_i\cdot \boldsymbol{b}_j=2\pi \delta_{ij} \)です。
ここで、\( \delta_{ij} \)はクロネッカーのデルタで、\( \boldsymbol{a}_1\)、\( \boldsymbol{a}_2\)、\( \boldsymbol{a}_3\)は単位胞の基本ベクトルです。
\( \boldsymbol{b}_1 \)と\( \boldsymbol{b}_2 \)と\( \boldsymbol{b}_3 \)は、次のようにして求められます。
まず、\( \boldsymbol{b}_1 \)についてのみ着目します。
\( \boldsymbol{a}_1\cdot \boldsymbol{b}_1 \)のみが\(0\)ではない値をもつということから、\( \boldsymbol{b}_1 \)は\( \boldsymbol{a}_2 \)と\( \boldsymbol{a}_3 \)に垂直であるということになります。
\( \boldsymbol{a}_2 \)と\( \boldsymbol{a}_3 \)の両方に垂直なベクトルの例といえば、両者の外積\( \boldsymbol{a}_2\times \boldsymbol{a}_3 \)があるため、\( \boldsymbol{b}_1 \)は\( \boldsymbol{a}_2\times \boldsymbol{a}_3 \)に平行だといえます。
その比例定数を\( \alpha \)とすると、\( \boldsymbol{b}_1\cdot \boldsymbol{a}_1=\alpha V=2\pi \)となるため、\(\displaystyle \alpha=\frac{2\pi}{V} \)と求められます。
ここで、\(V\)は3つのベクトル\( \boldsymbol{a}_1 \)、\( \boldsymbol{a}_2 \)、\( \boldsymbol{a}_3 \)で張られる平行六面体の体積です。
\( \boldsymbol{b}_2 \)と\( \boldsymbol{b}_3 \)についても同様に求めることができるので、逆格子ベクトル\(\displaystyle \boldsymbol{G}=\frac{2\pi}{V}h
\boldsymbol{a}_2\times \boldsymbol{a}_3+\frac{2\pi}{V}k\boldsymbol{a}_3\times \boldsymbol{a}_1+\frac{2\pi}{V}l\boldsymbol{a}_1\times \boldsymbol{a}_2 \)となります。
逆格子ベクトルの特徴
逆格子ベクトルの特徴は、次のように考えることができます。
まず、ラウエ指数と同じミラー指数である\( (h\ k\ l) \)面を考えます。
\( (h\ k\ l) \)面上の任意の点を与えるベクトルを\(\boldsymbol{p}\)、\( (h\ k\ l) \)面と平行なベクトルを\( \boldsymbol{p}_0 \)とします。
すると、\(x\)と\(y\)を任意の実数として、\(\displaystyle \boldsymbol{p}=\frac{\boldsymbol{a}_1}{h}+x(\frac{\boldsymbol{a}_2}{k}-\frac{\boldsymbol{a}_1}{h})+y(\frac{\boldsymbol{a}_3}{l}-\frac{\boldsymbol{a}_1}{h}) \)、\(\displaystyle \boldsymbol{p}_0=x_0(\frac{\boldsymbol{a}_2}{k}-\frac{\boldsymbol{a}_1}{h})+y_0(\frac{\boldsymbol{a}_3}{l}-\frac{\boldsymbol{a}_1}{h}) \)と表されます。
\( \boldsymbol{G}\cdot \boldsymbol{p}_0=0 \)となるため、逆格子ベクトル\(\boldsymbol{G}\)は\( (h\ k\ l) \)面と垂直の関係にあるということになります。
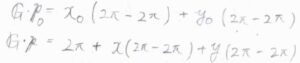
また、\( \boldsymbol{G}\cdot \boldsymbol{p}=2\pi \)であり、\(\boldsymbol{p}\)が\(\boldsymbol{G}\)と並行であるときの\(\boldsymbol{p}\)の大きさは、面の間隔である\( d_{hkl} \)と等しいため、逆格子ベクトル\(\boldsymbol{G}\)の大きさは\(\displaystyle \frac{2\pi}{d_{hkl}} \)だとわかります。
このことより、ラウエ指数とミラー指数には明確な違いがあるものの、密接な関係があると言えます。
そして、結晶の繰り返し構造はしばしば波と同じように考えることができますが、そのとき、逆格子ベクトルはその波の波数ベクトルに相当します。
それは、逆格子ベクトルの大きさである\(\displaystyle \frac{2\pi}{d_{hkl}} \)が、波長\( d_{hkl} \)の波の波数ベクトルの大きさであることから、容易にイメージできると思います。
ラウエ条件とブラッグの法則との関係
最後に、ブラッグの法則がラウエ条件から導けることを示します。
ラウエ指数をすべて\(n\)倍したとき、\(\displaystyle |\boldsymbol{G}|=\frac{2\pi}{d_{nh, nk, nl}}\)となります。
また、回折条件を満たすとき、\(\boldsymbol{q}=\boldsymbol{G}\)より、\(\displaystyle |\boldsymbol{G}|=\frac{4\pi}{\lambda}\sin{\theta}\)となります。
両者に\(\displaystyle \frac{\lambda d_{nh, nk, nl}}{2\pi}\)をかけると、\(\lambda=2d_{nh, nk, nl}\sin{\theta}\)となり、ブラッグの法則が導かれます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!