こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(rate equation)
それでは内容に入っていきます!
反応速度式
ここでは、下記の反応を例にします。
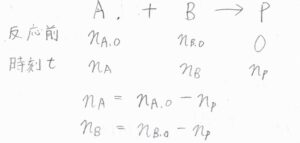
化学種\(\rm{A}\)と\(\rm{B}\)が1つずつ反応して、生成物\(\rm{P}\)(ができたというものです。
反応が起こる前の\(\rm{A}\)と\(\rm{B}\)の物質量をそれぞれ\(n_{\rm{A},0}\)、\(n_{\rm{B},0}\)、時刻\(t\)における\(\rm{P}\)の物質量を\(n_\rm{P}\)とすると、\(\rm{P}\)が生成した分だけ\(\rm{A}\)と\(\rm{B}\)は消費されたことになるため、時刻\(t\)における\(\rm{A}\)と\(\rm{B}\)の物質量はそれぞれ\(n_\rm{A,0}\)\(-n_\rm{P}\)、\(n_\rm{B,0}\)\(-n_\rm{P}\)と表されます。
ここで、最も簡単な反応機構でこの反応が起こっていると仮定します。
最も簡単な機構というのは、\(2\)分子が反応できるほど近づいたところで\(\rm{P}\)に変化するというものです。
その場合、反応が起こる確率は\(2\)分子の衝突確率に比例します。
衝突確率は、分子数に比例して大きくますが、体積が大きくなるとそれに反比例して小さくなります。
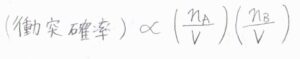
これを\(\rm{A}\)と\(\rm{B}\)の両方について考えるので、衝突確率は両者それぞれのモル濃度に比例するということになります。
これ以降、モル濃度は大かっこで表すことにします。
\(\rm{P}\)の生成速度を\(v\)を、\(\rm{P}\)のモル濃度を時間について微分したものだと定義すると、これが\([\rm{A}]\)と\([\rm{B}]\)の両方に比例することになります。

\(k\)は比例定数で、反応速度定数と呼ばれます。
ここで、\(V\)は体積です。
またお話ししますが、反応速度定数は温度や分子の形などを反映した値になります。
それで、\(\rm{P}\)の生成速度とまったく同じ速度で\(\rm{A}\)と\(\rm{B}\)は消費されていくことから、これらの消滅速度は\(-v\)で書けます。
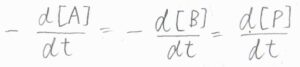
より一般的に、\(\displaystyle \sum_\rm{J}\)\(\nu_\rm{J}\)\( \rm{J}\)\(=0\)という反応式を考える際には、まず反応進行度\(\xi\)を反応に関わるすべての化学種について\(\rm{d}\)\(n_\rm{J}\)\(=\nu_\rm{J}\)\(\rm{d}\)\(\xi\)となるように定義します。
さらに、反応速度\(v\)は\(\displaystyle \frac{1}{V}\frac{\rm{d}\xi}{\rm{d}\mathit{t}}\)と定義します。
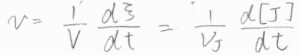
また、これは\(\displaystyle \frac{1}{\nu_\rm{J}}\frac{\rm{d} [\rm{J}]}{\rm{d}\mathit{t}}\)とも表されます。
そして、理想気体については、理想気体の状態方程式より\([\rm{J}]\)を\(\displaystyle \frac{p_\rm{J}}{RT}\)と書き換えることができます。
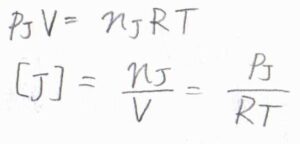
ここで、\(p_\rm{J}\)は化学種\(\rm{J}\)の分圧、\(R\)は気体定数、\(T\)は絶対温度です。
反応が起こっている間、温度が一定だったときには、\(\displaystyle v=\frac{1}{\nu_\rm{J}\mathit{RT}}\frac{\rm{d}\mathit{p}_J}{\rm{d}\mathit{t}}\)となります。

反応次数
ここまでは単純な反応機構でしたが、より一般的な反応では反応速度\(\displaystyle v\)がモル濃度に比例するとは限りません。
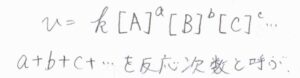
それぞれの化学種のモル濃度の指数をすべて足したものは反応次数と呼ばれ、反応次数が\(1\)の反応は\(1\)次反応、反応次数が\(2\)の反応は\(2\)次反応と言います。

反応次数、そしてそれぞれのモル濃度についての依存性は、反応機構に依存するため、全体の化学反応式からは決めることができず、実験的に求めることになります。
つまり、\(\rm{A}\)\(+\rm{B}\)\( \longrightarrow \rm{P}\)という反応式を見て、反応速度\(v=k[\rm{A}\)\(][\rm{B}]\)だと決めつけることはできません。
モル濃度の測定方法
それでは、反応次数を実験的に決定する方法について考えていきましょう。
反応次数を考える前には、まずモル濃度を測定しなくてはいけません。
実時間分析
始めに、モル濃度をリアルタイムで測定する方法について説明します。
この方法は実時間分析と呼び、次に紹介する流通法やストップトフロー法があります。
流通法
流通法では\(\rm{A}\)と\(\rm{B}\)を一定の速度で流入させて混合し、流出してきたもののモル濃度を分光器を使って調べます。
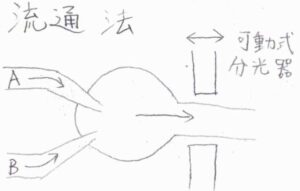
この分光器は図中でいうところの左右に移動することができて、左右に動かすことで、反応開始からどれだけ経過した時点を観察するかをコントロールできます。
ただし、この方法では、常に反応物を供給する必要があるため、多量の反応物が必要になります。
また、反応を追えるほど流速を速く保つ必要があるため、あまりに高速で反応が進行する場合にはこの方法は使えません。
ストップトフロー法
ストップトフロー法では、反応物を一瞬だけ流入させて混合し、それを流出させます。
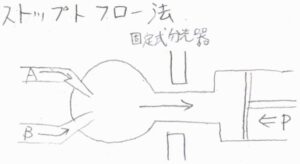
分光器は固定されており、リアルタイムでモル濃度を観察します。
紫外可視吸収、円二色性、蛍光分光などの分光技術が使われます。
試料が少量で済むことから、生化学反応の観察に適しており、たんぱく質のフォールディングや酵素反応の速度論の研究に使われています。
ミリ秒から秒の時間スケールで起こる反応に使うことができます。
閃光光分解
ピコ秒やフェムト秒単位で起こるような超高速反応では、閃光光分解という方法もあります。
始めに試料にパルス波を照射することで反応を開始させ、そこに波長の異なる電磁波を照射するなどしてモル濃度を調べます。
電子吸収および放出、赤外吸収、ラマン散乱などが利用されます。
分光器によるモル濃度測定
分光器でモル濃度を決定する原理は、例えば吸収分光法だと、ランベルト-ベールの法則を利用しています。

モル濃度が大きいほど、特定の波長の電磁波を多く吸収するため、入射光と透過光の強度に大きな差が生じます。

他の分光法でも、強度を利用してモル濃度を決定しています。
急速停止法
続いて、実時間分析とは異なる方法として、急速停止法というものがあります。
反応が起こっている途中で、急激に冷却したり、停止剤を加えたりすることにより反応を停止させる方法です。
急冷する場合を急冷停止法、停止剤を使う場合を化学的急速流動停止法と言います。
反応停止にかかるミリ秒単位の時間スケールよりも反応が速い場合には、使うことができません。
実時間分析と異なり、測定にはいくら時間をかけてもよいため、滴定やクロマトグラフィー、ゲル電気泳動などの方法で物質量を決定することができます。
反応によっては、反応物や生成物に加えて中間体の濃度を測定することも可能です。
反応次数の決定方法
これらの方法を用いて反応次数を求める際には、次のような手段があります。
過剰法
まず、過剰法という方法では、反応速度のモル濃度依存性を調べたい1つの化学種を除き、他すべての化学種の濃度を過剰にします。

このとき、反応の進行に伴って濃度が変化するのは、いま着目している1つの化学種だけだと考えることができます。
他の化学種の濃度をすべて定数とみなして、反応速度定数と同じように扱うことにします。
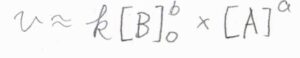
グラフで縦軸に反応速度の常用対数、横軸にいま着目している化学種のモル濃度の常用対数をとると、直線が書けます。

その傾きが指数になります。
傾きが\(1\)の反応のことを擬\(1\)次反応、傾きが\(2\)の反応を擬\(2\)次反応と言います。
擬と付いているのは、実際に\(1\)次、\(2\)次であるというわけではなく、見かけ上そうなっているという意味です。
初速度の方法
過剰法とは別の方の方法で、初速度の方法というものもあります。
反応開始直後の短い時間では、濃度が初濃度、ここでは\([\rm{A}\)\(]_0\)にほぼ等しいと近似できます。
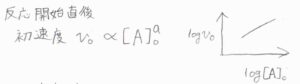
初濃度を変化させながら反応速度を調べて、それを両対数グラフにプロットすれば、過剰法と同様に直線の傾きから依存性を調べることができます。
積分型反応速度式
最後に、モル濃度がどのように時間変化するのかを考えて終わります。
1次反応
ここでは反応物\(\rm{A}\)の\(1\)分子が生成物\(\rm{P}\)の\(1\)分子に変化するという\(1\)次反応を考えてみます。
![]()
反応速度は、\(\rm{A}\)のモル濃度の消滅速度にマイナスをかけたものであり、これが\(k[\rm{A}]\)で表されます。
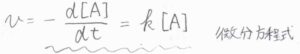
波線部を見ると、微分方程式になっていることがわかります。
両辺を時刻\(0\)から\(t\)まで定積分すると、結局\([\rm{A}\)\(]=[\rm{A}\)\(]_0\exp{(-kt)}\)となります。
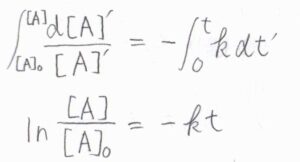
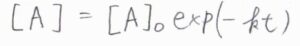
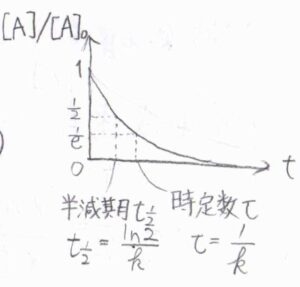
モル濃度が\(\displaystyle \frac{1}{2}\)倍になるまでにかかる時間を半減期といい、それは\(\displaystyle \frac{\ln{2}}{k}\)と書けます。
また、モル濃度が\(\displaystyle \frac{1}{\rm{e}}\)倍になるまでにかかる時間を時定数と呼び、それは\(\displaystyle \frac{1}{k}\)と表せます。
2次反応
続いて、反応物\(\rm{A}\)が\(2\)分子から生成物\(\rm{P}\)が\(1\)分子生成する\(2\)次反応について考えてみます。

この場合も微分方程式になるので、これを解くと、\(\displaystyle [\rm{A}]=\frac{[\rm{A}]_0}{1+[\rm{A}]_0\mathit{kt}}\)という関係が得られます。
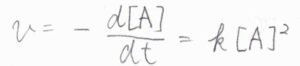
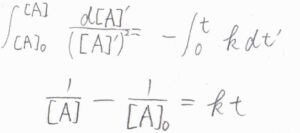
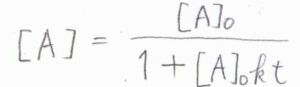
反比例のグラフを平行移動した形の減衰曲線になります。
最後、異なる化学種\(\rm{A}\)と\(\rm{B}\)が\(1\)分子ずつ反応して生成物\(\rm{P}\)が\(1\)分子できるという\(2\)次反応については、以下のようになります。

\([\rm{A}]\)の減少量を\(x\)とおくと、\([\rm{B}]\)の減少量も\(x\)となるので、ここから微分方程式を解いていきます。
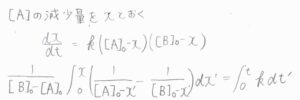
すると、\(\displaystyle \frac{1}{[\rm{B}]_0-[\rm{A}]_0}\ln{\frac{[\rm{B}]/[\rm{B}]_0}{[\rm{A}]/[\rm{A}]_0}}=\mathit{kt}\)という関係式が導かれます。
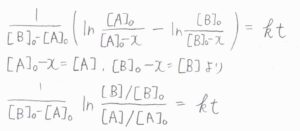
過剰法でやったように、\([\rm{B}]_0\)がとても大きいとして近似すれば、\([\rm{A}]\)は指数関数になり、見かけ上は\(1\)次反応と同じふるまいをします。
\([\rm{A}]_0\)がとても大きいとしても、\([\rm{B}\)\(]_0-[\rm{A}]_0\)が負の値となるため、\([\rm{B}]\)は指数関数となり、時間の経過とともに減衰します。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!