こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓

動画で使ったシートはこちら(phase separation)
それでは内容に入っていきます!
過剰熱力学量
まず、理由は後でも述べますが、理想溶液では相分離が起こりません。
理想溶液については、こちらを参照してください。

そこでここでは、実在溶液を含む一般的な溶液について考える方法から話していきます。
理想溶液と実在溶液の熱力学量の差は、過剰熱力学量として定義されます。
つまり、ある熱力学量\(X\)について、過剰熱力学量\(X^\rm{E}\)は、混合に伴う変化量\(\Delta X\)から理想溶液の値\(\Delta X^\rm{ideal}\)を引いた値となります。

例えば、過剰エントロピー\(S^\rm{E}\)は実際の混合エントロピー変化から\(\displaystyle -nR\sum_i x_i\ln{x_i}\)を引いた値です。

また、理想溶液の混合エンタルピーと混合による体積変化は\(0\)ですから、これらがそのまま過剰エンタルピー、過剰体積となります。
正則溶液
そして、特に過剰エントロピーが\(0\)で過剰エンタルピーが\(0\)ではない溶液のことを正則溶液と呼びます。

物理的な意味としては、同種分子間相互作用と異種分子間相互作用に差があるが、その相互作用はロンドン分散力のみであり、錯形成などはないということです。
それで、混合エンタルピーをどのように表すのかということですが、まず示量性の量なので、全体の物質量\(n\)に比例します。
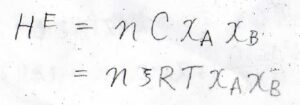
それから、分子間相互作用であることから、各成分の分子数にも比例するはずなので、モル分率\(x_\rm{A}\)と\(x_\rm{B}\)の両方に比例します。
したがって、比例定数を\(C\)とすると、\(H^\rm{E}\)\(=nCx_\rm{A}\)\(x_\rm{B}\)という関係が成り立つことになります。
ここで、\(C\)はエネルギーの単位をもつ量です。
よって、\(1\ \rm{mol}\)の分子がもつ熱運動エネルギー\(RT\)を使うと、\(H^\rm{E}\)\(=n\xi RTx_\rm{A}\)\(x_\rm{B}\)という形でも表すことができます。
ここで、\(\xi\)は無次元量で、同種分子間相互作用と異種分子間相互作用の差を反映したパラメータとなります。
横軸を\(\rm{A}\)のモル分率、縦軸を混合エンタルピーとすると、下のようなグラフが書けます。
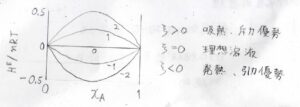
グラフに打ってある数字は、\(\xi\)の値を表しています。
\(\xi=0\)というのが、理想溶液に対応します。
\(\xi\)が負というのは、分子間で引力が優勢となることを意味します。
このとき、2つの成分の混合は発熱を伴う変化になります。
反対に、\(\xi\)が正のときには、分子間で斥力が優勢であり、混合は吸熱を伴う変化になります。
そして、エントロピーも加味して、正則溶液の混合ギブズエネルギー\(\Delta_\rm{mix}\)\( G\)を\(\xi\)を使って表すと、\(nRT(\xi x_\rm{A}\)\(x_\rm{B}\)\(+x_\rm{A}\)\(\ln{x_\rm{A}}\)\(+x_\rm{B}\)\(\ln{x_\rm{B}})\)となります。

この関数のグラフを書くために、組成比についての微分も考えると、次のような事実が導かれます。
まず、エンタルピー項を\(x_\rm{A}\)について微分し、その両端の極限をとると、\(n\xi RT\)という有限の値になります。
これに対して、混合エントロピーの導関数は、両端で\(\infty\)となります。
有限量から無限量を引くと無限量になるため、混合ギブズエネルギーの導関数は両端で\(-\infty\)に発散します。
これはつまり、組成比が\(0\)または\(1\)付近を見ると、混合ギブズエネルギーが負となるような組成の領域が必ず存在するということです。
わかりやすく言い換えれば、どれだけ相性の悪い成分の組み合わせでも、少しだけなら混ざるということです。
水と油を混ぜたら分離しますが、水層にも少し油の分子が混ざっていて、油層にも少し水が混ざっています。
実際に、横軸を\(\rm{A}\)のモル分率、縦軸を混合ギブズエネルギーとして、グラフを書くと、このようになります。

\(\xi\)が負のときには、エンタルピーが下に凸、エントロピーが上に凸となるため、ギブズエネルギーは下に凸となります。
ただ、\(\xi\)が正のときには、エンタルピーが上に凸となるため、エントロピーとの大小関係によっては、このように極小が2つあるグラフになることがあります。

このようなポテンシャルカーブは、そのまま双極小型であると言います。
相分離の原理
このグラフを使えば、正則溶液でなぜ相分離が起こるのかを説明することができます。
それを説明するためには、分子のブラウン運動が重要になります。
すべての分子は熱エネルギーをもっており、ランダムな動きをします。
その影響で、一度均質となった溶液でも、瞬間的に見れば、部分的に濃度の高い領域と濃度の低い領域が生じることになります。
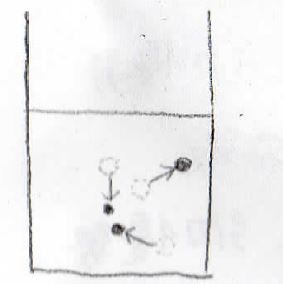
この現象を濃度揺らぎと言います。
これにより、例えば溶液に光を当てると、溶質分子の振動によるドップラー効果が生じたりします。
動的光散乱測定は、このドップラー効果を散乱高強度あるいは散乱光電場の自己相関関数という形で観察し、緩和時間から流体力学的半径を決定できるというしくみです。
ここについては、また高分子の話で詳しくお話しする予定です。
話が逸れましたが、ここで注目してもらいたいのは、瞬間的に濃度の高い領域と濃度の小さい領域ができたときに、全体のギブズエネルギーがどうなるのかということです。
相分離が起こるかどうかは、混合ギブズエネルギーのグラフの形で決まります。
グラフが下に凸のときには、もとの組成を中心に、同じ幅だけずれた2点へ濃度が移ります。
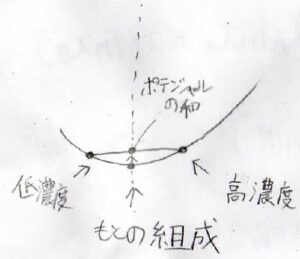
このとき、全体のギブズエネルギーは、この2点を結ぶ直線ともとの組成を示す直線の交点になります。
グラフが下に凸の場合、この平均値は均一なときの値から大きくなります。
つまり、濃度差がある状態は熱力学的に不利だということです。
すると、もとに戻ろうとする復元力が分子にはたらくため、巨視的には均一な溶液のままとなります。
対して、ギブズエネルギーが上に凸な場合は、濃度差が生じることで、全体のギブズエネルギーが減少します。
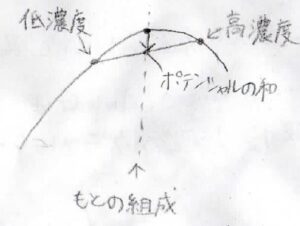
つまり、濃度差が生じたほうが熱力学的に有利だということです。
こうなると、濃度揺らぎがさらなる濃度差を生じさせるため、一度均一に混ざったとしても、相分離が起こります。
練習問題
それでは最後に、練習問題をやって終わります。
先ほど、分子間で斥力相互作用が優勢のとき、エンタルピーとエントロピーの大小関係によって、ギブズエネルギーのグラフがどうなるか決まるという話をしました。
ここでは、正則溶液で相分離が起こるための\(\xi\)の条件を具体的に求めてみてください。

組成が\(0\)や\(1\)のときには、必ず下に凸となるので、変曲点を2つもつことが必要になります。
混合ギブズエネルギーを\(x_\rm{A}\)について微分すると、\(nRT[\xi-2\xi x_\rm{A}\)\(+\ln{x_\rm{A}}-\ln{(1-x_\rm{A})}]\)となります。
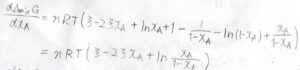
これをもう一度微分すると、\(\displaystyle nRT(-2\xi+\frac{1}{x_\rm{A}}+\frac{1}{1-x_\rm{A}})\)となります。
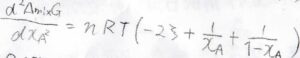
これが\(0\lt x_\rm{A}\)\(\lt 1\)の範囲に、異なる2つの実数解をもてばよいことになります。
この関数は連続関数であり、両端で無限大に発散、さらに\(x_\rm{A}\)\(=0.5\)の直線を中心に線対称となっているため、\(x_\rm{A}\)\(=0.5\)を代入したときの値が負となるための条件を考えます。
\(x_\rm{A}\)\(=0.5\)をこの2階偏導関数に代入すると、\(nRT(-2\xi+2+2)\)となり、これが負ということです。
したがって、\(\xi\gt 2\)というのが相分離するために\(\xi\)が満たす条件だと導かれます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!