こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
指標表の意味については、こちらの記事で解説しております。

動画はこちら↓
動画で使ったシートはこちら(how to use character table 1、how to use character table 2)
始めに
点群の内容は、手元に分子模型があったほうが圧倒的に理解しやすいです。
5000円前後でおすすめの分子模型があったので、ここで紹介しておきます。
積分の消滅
まず、関数の対称性と積分の値との関係について考えましょう。
\(xy\)平面に2つの円があったとして、重なっている部分の面積を\(I\)とします。
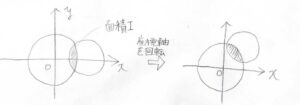
この\(I\)は、どれだけ回転や鏡映をとって座標軸を動かしても、面積なのでその値は変化しません。
そこで、\(I\)は\(\rm{A}_1\)の対称性をもつ既約表現の基底とみなすことができます。
これを三次元空間における原子軌道の重なりと同じように考えると、まず\(I\)は波動関数\(f_1\)と\(f_2\)の積を全空間で積分したものとして与えられます。
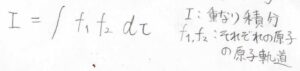
これが\(\rm{A}_1\)の対称性をもっているときだけ、\(0\)ではない値をもつことになります。
体積素片\(\rm{d}\)\(\tau\)は座標軸に依存しないため、関数の積\(f_1f_2\)の対称性が重要となります。
\(f_1f_2\)が\(\rm{A}_1\)の基底となるかどうかは、次のような方法で確認します。
まず、\(f_1\)と\(f_2\)の指標を別々の行に書きます。
次に、それぞれの対称操作について、指標の積を計算します。
これが\(f_1f_2\)の指標となるので、最後にこれが、\(\rm{A}_1\)の指標を含む和として書けるかどうかの判定をします。
例えば、\(C_\rm{3v}\)群に属する分子\(\displaystyle \rm{AB}_3\)について、原子\(\displaystyle \rm{B}\)3つの\(\rm{s}\)軌道からできた\(\rm{A}_1\)の既約表現の基底を\(f_1\)、中心原子\(\displaystyle \rm{A}\)の\(\displaystyle \rm{s}\)軌道を\(f_2\)とすると、その積の指標は、\(1\)、\(1\)、\(1\)となります。

これは\(\rm{A}_1\)の指標と一致するので、この重なり積分は\(0\)以外の値をとりうることになります。
ここで、単純に\(\displaystyle \rm{A-B}\)間の距離がとても長いときには、\(\rm{A}_1\)の指標をもっていても重なりは\(0\)になるため、\(0\)以外の値をとりうる、という言い方をしています。
別のパターンとして、\(f_1\)が\(\rm{A}_2\)の既約表現の基底であった場合には、\(f_1f_2\)の指標が\(\rm{A}_2\)のものと一致します。
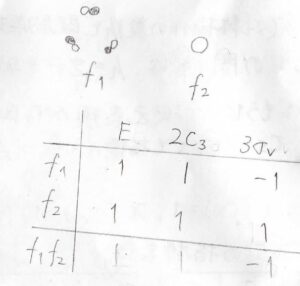
このときには、\(\rm{A}_1\)の指標を含まないので、積分は\(0\)になると断定することができます。
直積の分解
ここまでは、\(f_1f_2\)の指標がいずれかの対称種の値と一致するものでしたが、多くの場合、\(f_1f_2\)は既約表現の和を張ります。
アンモニア分子を例にして、\(f_1\)と\(f_2\)を対称種\(\rm{E}\)の基底の1つとして考えると、その指標の積は、\(4\)、\(1\)、\(0\)となります。
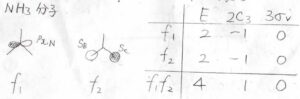
当然ですが、\(C_\rm{3v}\)群の対称種に四次元表現はないため、一致するものはありません。
しかし、実は\(4\)、\(1\)、\(0\)というのは、対称種\(\rm{A}_1\)と\(\rm{A}_2\)と\(\rm{E}\)の指標の和になります。

既約表現の和を張るとは、上記のように複数の指標の和が指標になるということです。
そして、この結果をまとめるために、\(\rm{E}\)\( \times \rm{E}\)\(=\rm{A}\)\(_1+\rm{A}\)\(_2+\rm{E}\)という書き方をし、この操作を直積の分解といいます。
ここで出てくる\(\times\)と\(+\)は通常の掛け算や足し算の記号ではなく、行列を用いた直積と直和という操作を表したもので、区別をするために、\(\bigotimes\)や\(\bigoplus\)で表記されることも多いです。
結局、この積が\(\rm{A}_1\)を含む和で書けたことから、その積分が\(0\)ではない値をとりうるということになります。
さらに、\(f_1f_2\)がもっと大きな数字の指標をもっているときには、どんな直和に分解できるのかがわかりにくくなります。
そこで、一般的な分解の方法も紹介します。
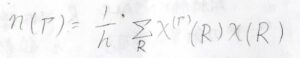
式で書くと上のとおりで、\(R\)が対称操作、\(\chi\)が指標、\(\Gamma\)が着目する既約表現、\(n\)がその既約表現が直和に現れる回数を指します。
煩雑に思えますが、実際は表を使ってとても簡単に分解できます。
例として、ここでは\(C_\rm{2v}\)群において、\(f_1f_2\)の指標が\(8\)、\(-2\)、\(-6\)、\(4\)となったときに、直和に\(\rm{A}_2\)がいくつ現れるのかを求めてみます。

ただし、対称操作の順番は、恒等操作、\(2\)回回転操作、\(\sigma_\rm{v}\)面についての鏡映操作、\(\sigma_\rm{v}’\)面についての鏡映操作という順番です。
\(C_\rm{2v}\)群では問題になりませんが、すべての対称操作を書かないといけないため、同じ類に属する対称操作もそれぞれ書くことに注意してください。
まず、積と\(\rm{A}_2\)の指標を2つの行に書きます。
そして、各列でその指標の積を計算して、下の行に書きます。
最後に、下の行の指標の和を取り、それを位数で割ります。
ここでは、\(8-2+6-4=8\)となり、これを位数\(4\)で割って\(2\)と計算されるので、\(f_1f_2\)を和に分解すると\(\rm{A}_2\)は2回出てくるということになります。
直交系の構築
次に、対称性の考え方を利用してLCAOの構築をするという話をしていきます。
シュレディンガー方程式は、多体問題を解くことができないため、ボルン-オッペンハイマー近似をしたとしても、原子核1つ、電子1つという水素様原子しか扱えません。

そこで、分子の波動関数を考える際には、もともとの原子の波動関数の線形結合として近似する方法があります。
この近似のことをLCAO近似と言います。
LCAOはLinear Combination of Atomic Orbitals、つまり原子軌道の線形結合という意味です。
それぞれの原子の波動関数について、ことなるものの積を全空間で積分したときに\(0\)となる関係のことを直交すると言い、直交する関数だけでできた関数形のことを直交系といいます。
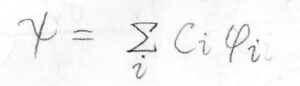
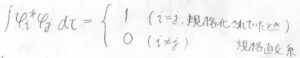
さらにそれぞれが規格化されている場合は、規格直交系といいます。
規格直交系であれば、分子の波動関数\(\psi\)同士の内積が、それぞれの係数の\(2\)乗の和になるなど、式をシンプルにできるので、とても便利です。
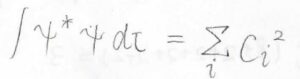
仮に、\(\varphi_i\)と\(\varphi_j\)が同じ指標をもっていたときには、その積の指標に\(\rm{A}_1\)の指標が必ず含まれます。
これは、とても簡単に証明できるので、この記事の前半部分を参照して考えてみてください。
そしてこのことより、\(i\)と\(j\)が異なるときには、必ず\(\varphi_i\)と\(\varphi_j\)は異なる指標をもっていないと直交系にならないことになります。
互いに異なる指標をもっている波動関数は、対称適合線形結合、略してSALCというものを構築することで、見つけられます。
これから紹介するのは、任意の基底から、既約表現の基底となるような線形結合を作る方法です。
これまで、\(C_\rm{2v}\)群と\(C_\rm{3v}\)群で、下のような形の軌道が基底になるとお話ししてきたのですが、これらの係数を指標表を使って決定します。
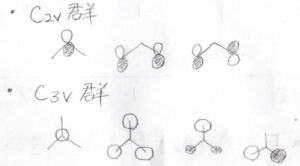
それぞれの基底同士は線形独立であるため、LCAO構築のための構成単位となります。
まず、これがSALC構築のための式です。

\(R\)が対称操作、\(\Gamma\)が着目している対称種の既約表現、\(h\)が位数、\(\chi\)が指標、\(\psi_m\)がSALC、\(\chi_0\)が先に与えた任意の基底を並べたベクトルです。
\(P^{(\Gamma)}\)は既約表現\(\Gamma\)の射影演算子といいます。
煩雑な形ですが、試しに\(\displaystyle \rm{SO}_2\)分子について、\(\rm{A}_2\)の既約表現の基底を求めてみましょう。
表を作るのですが、まずはいちばん左の列にすべての対称操作を書きます。

同じ類に含まれているものも区別して書いてください。
それから上の行に任意の基底を書きます。
ここでは、それぞれの原子の\(\rm{p}\)\(_y\)軌道としています。
それから、それぞれの対称操作により、任意の基底がどのように変化するのかを書き込みます。
例えば、\(2\)回回転操作を行った後、\(\displaystyle \rm{A}\)の酸素原子上には、\(\displaystyle \rm{B}\)の酸素原子上にあった軌道が来ます。
またそのとき、位相も反転するので、\(p_{y, \rm{A}}\)は\(-p_{y, \rm{B}}\)となります。
そして、このように作った表について、今着目している対称種\(\rm{A}_2\)の指標をかけていきます。
\(\rm{A}_2\)の指標は、順番に\(1\)、\(1\)、\(-1\)、\(-1\)であるため、\(\sigma_\rm{v}\)と\(\sigma_\rm{v}’\)の行の符号を変えます。

それから、各列について和をとります。
すると、\(p_{y, \rm{S}}\)の列は\(0\)、\(p_{y, \rm{A}}\)の列は\(2p_{y, \rm{A}}\)\(-2p_{y, \rm{B}}\)、\(p_{y, \rm{B}}\)の列は\(2p_{y, \rm{B}}\)\(-2p_{y, \rm{A}}\)となります。
ここで、\(0\)というのは規格化条件を満たしませんし、\(2p_{y, \rm{A}}\)\(-2p_{y, \rm{B}}\)を\(-1\)倍したものが\(p_{y, \rm{B}}\)\(-2p_{y, \rm{A}}\)ですから、線形独立になりません。
したがって、線形独立なのは\(2p_{y, \rm{A}}\)\(-2p_{y, \rm{B}}\)の1つであり、最後にこれを位数の\(4\)で割った\((1/2)(p_{y, \rm{A}}-\)\(p_{y, \rm{B}})\)が\(\rm{A}_2\)の対称性をもつSALCとして求められます。
ただし、このSALCは対称性だけを考えてできたものなので、規格化条件を満たすための係数は、ここから全空間について積分して求めることになります。
選択律
それでは、最後に選択律の話をします。
化学における選択律は、2つの量子状態間の遷移が許されるのかどうかを簡潔に表した規則のことを指します。
遷移が許されていることを許容、許されていないことを禁制といいます。
状態\(1\)から状態\(2\)へ分子遷移することで生じるスペクトルの強度\(I\)は、遷移確率に比例しますが、それはこちらの式で書かれる遷移双極子モーメントの大きさの\(2\)乗に比例すると近似されます。
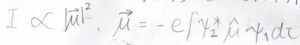
ここで、古典的な電気双極子モーメントの大きさは、電荷と原子間距離の積であるため、\(\hat{\mu}\)には座標が入ります。
同時に、\(\hat{\mu}\)はハミルトニアンの一次の摂動、つまりは相互作用に関係しています。
その相互作用とは、光吸収や発光を伴う遷移の場合は、電子と光子との相互作用を指します。
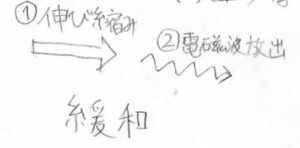
遷移によって双極子が変化した場合、電場と磁場に揺らぎが生じるため、これが電磁波として放出されます。
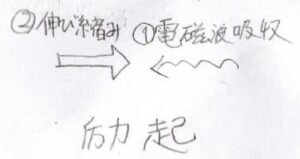
逆に電磁波を吸収するということは、双極子に変化を与えることになります。
実際に選択律を導くためには、\(\psi_1\)、\(\hat{\mu}\)、\(\psi_2\)これら3つの積を和に分解して、\(\rm{A}_1\)が含まれるかを調べます。
含まれている場合は許容遷移、含まれていない場合は禁制遷移となります。
ただし、禁制遷移でもあくまで一次の項までの摂動で近似した場合の理論上の遷移確率が\(0\)となったというだけであって、絶対に遷移が起こらないとは限らないので、注意してください。
許容遷移よりも著しく遷移確率が低いのが禁制遷移というくらいに認識しておいてください。
練習問題
最後に、練習問題をやってみましょう。
(1-1) \(C_\rm{3v}\)群に属する分子で、積の指標が\(8\)、\(2\)、\(2\)となったとき、\(f_1f_2\)はどんな既約表現の和を張りますか?
ただし、対称操作の順番は、恒等操作、\(3\)回回転操作、鏡映操作の順番です。
(1-2)\(C_\rm{2v}\)群について、中心原子の\(d_{z^2}\)軌道、\(x\)、\(d_{xy}\)軌道という3つの関数の積を全空間で積分したときに\(0\)になることを示してください。
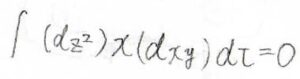
(2-1)アンモニア分子について、対称種\(\rm{E}\)のSALC2つを求めてください。
(2-2)は、\(O_\rm{h}\)群に属する\(\displaystyle \rm{SF}_6\)分子について、中心に向いた6つのフッ素原子の\(2\rm{p}\)軌道は\(\rm{A}\)\(_\rm{1g}\)\(+\rm{E}\)\(_\rm{g}\)\(+\rm{T}\)\(_\rm{1u}\)を張ります。
そのとき、硫黄原子の原子軌道の中で、それぞれがどの対称性をもった波動関数と\(0\)ではない重なりをもつことになるでしょうか?
\(O_\rm{h}\)群の指標表は記事内で出していないので、教科書等の巻末部分を利用するなどしながら考えてください。
(2-3)正四面体の環境で中心原子の\(\rm{p}\)\(_x\)軌道から\(\rm{p}\)\(_y\)軌道への遷移が許容であるか禁制であるかを判定してください。

ここで、\(3\)回回転操作2つと鏡映操作3つはそれぞれ区別して書くことに注意してください。
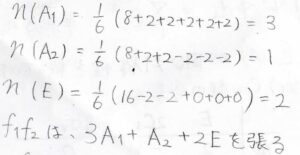
まず、\(\rm{A}_1\)の個数を求める式は、\(\displaystyle \frac{8+2+2+2+2+2}{6}=3\)となります。
\(\rm{A}_2\)については、\(\displaystyle \frac{8+2+2-2-2-2}{6}=1\)となります。
最後、\(\rm{E}\)については\(\displaystyle \frac{16-2-2+0+0+0}{6}=2\)となります。
これらの結果をまとめると、\(f_1f_2\)は\(3\rm{A}\)\(_1+\rm{A}\)\(_2+2\rm{E}\)を張るということになります。
(1-2)では、積分が\(0\)になることを示すために、この関数の積を直和に分解して\(\rm{A}_1\)が含まれないことを確かめてみましょう。
3つの関数の積になってもやり方はまったく同じで、それぞれの指標の積が、積の指標となります。
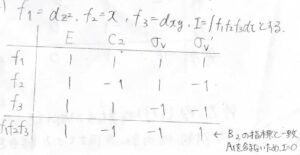
計算すると、\(1\)、\(-1\)、\(-1\)、\(1\)となり、これは\(\rm{B}_2\)の指標と一致しています。
したがって、直和に\(\rm{A}_1\)は1回も出てこないため、これを全空間で積分しても\(0\)になることがわかります。
(2-1)は、\(C_\rm{3v}\)群について、まずすべての対称操作をいちばん左の列に書きます。

そして、任意の基底はそれぞれの原子の\(\rm{s}\)軌道としておきます。
そして、それぞれの対称操作でどこに移されるのかというのを書きます。
対称種\(\rm{E}\)の指標は恒等操作で\(2\)、2つの\(3\)回回転操作で\(-1\)、3つの鏡映操作で\(0\)ですから、これをそれぞれの行にかけていきます。
それから、それぞれの列の和をとると、\(s_\rm{N}\)の列は\(0\)、\(s_\rm{A}\)の列は\(2s_\rm{A}\)\(-s_\rm{B}\)\(-s_\rm{C}\)、\(s_\rm{B}\)の列は\(2s_\rm{B}\)\(-s_\rm{C}\)\(-s_\rm{A}\)、\(s_\rm{C}\)の列は\(2s_\rm{C}\)\(-s_\rm{A}\)\(-s_\rm{B}\)となります。
ここで、\((2s_\rm{A}\)\(-s_\rm{B}\)\(-s_\rm{C}\)\()+(2s_\rm{B}\)\(-s_\rm{C}\)\(-s_\rm{A}\)\()=-(2s_\rm{C}\)\(-s_\rm{A}\)\(-s_\rm{B}\)\()\)となってしまうため、これらは線形独立ではありません。
そこで、\(2s_\rm{B}\)\(-s_\rm{C}\)\(-s_\rm{A}\)と\(2s_\rm{C}\)\(-s_\rm{A}\)\(-s_\rm{B}\)の差をとると、\(3s_\rm{B}\)\(-3s_\rm{C}\)が出てくるのですが、これは\(2s_\rm{A}\)\(-s_\rm{B}\)\(-s_\rm{C}\)と線形独立になります。
したがって、これらを位数の\(6\)で割って出てくる\(\displaystyle \frac{1}{6}(2s_\rm{A}\)\(-s_\rm{B}\)\(-s_\rm{C}\)\()\)と\(\displaystyle \frac{1}{2}(s_\rm{B}\)\(-s_\rm{C}\)\()\)が対称種\(\rm{E}\)の2つのSALCということになります。
(2-2)は始めに問題の意味を解説すると、次のようになります。
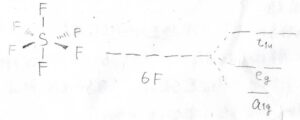
6つのフッ素原子について、中心を向いた6つの\(\rm{p}\)軌道から\(\rm{A}\)\(_\rm{1g}\)の基底となる1つの\(a_\rm{1g}\)軌道と\(\rm{E_g}\)の基底となる2つの\(e_\rm{g}\)軌道、\(\rm{T}\)\(_\rm{1u}\)の基底となる3つの\(t_\rm{1u}\)軌道ができました。
このときに、中心の硫黄原子の原子軌道がそれぞれどの軌道と結合をつくるのかというのを聞いています。
硫黄原子については、最外殻の\(3\rm{s}\)軌道、\(3\rm{p}\)軌道、\(3\rm{d}\)軌道を考えることにします。
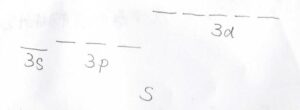
これらの原子軌道は全部で9個あるので、このうちの3個は結合を作らず、非結合性軌道になります。
まず、中心原子の\(\rm{s}\)軌道は、どんな対称操作をやっても位相は変化しませんから\(\rm{A}\)\(_\rm{1g}\)の対称性をもつことがすぐにわかります。
それから、\(O_\rm{h}\)群の指標表を見ると、対称種\(\rm{T}\)\(_\rm{1u}\)の既約表現の座標は\((x, y, z)\)とあるので、\(3\rm{p}\)\(_x\)軌道、\(3\rm{p}\)\(_y\)軌道、\(3\rm{p}\)\(_z\)軌道の3つが基底となることがわかります。
そして、対称種\(\rm{T}\)\(_\rm{2g}\)の座標の二次の項には\((xy, xz, yz)\)とあるため、\(3\rm{d}\)\(_{xy}\)軌道、\(3\rm{d}\)\(_{xz}\)軌道、\(3\rm{d}\)\(_{yz}\)軌道が3つの基底となります。
これはフッ素原子の軌道にはない対称種のため、非結合性軌道となります。
そして、残った\(3\rm{d}\)\(_{x^2-y^2}\)軌道と\(3\rm{d}\)\(_{z^2}\)軌道が\(\rm{E_g}\)の基底2つとなります。
以上のことをまとめると、\(0\)ではない重なりをもつ組み合わせは、\(3\rm{s}\)と\(a\)\(_\rm{1g}\)、\(3\rm{p}\)と\(t\)\(_\rm{1u}\)、\(3\rm{d}\)と\(e_\rm{g}\)となります。
(2-3)は、\(T_\rm{d}\)群について\(f_1=p_x\)、\(f_2=z\)、\(f_3=p_y\)としてそれらの積の指標を計算します。

すると、順番に\(27\)、\(0\)、\(-1\)、\(-1\)、\(1\)となります。
これに\(\rm{A}_1\)の指標をかけたものも同じになります。
最後、同じ類のものも区別してこれらすべての和をとると、\(24\)になります。
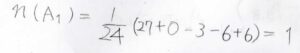
これを\(T_\rm{d}\)群の位数である\(24\)で割って、\(1\)となります。
すなわち、これらの積は\(\rm{A}_1\)を和に含んでいることになるので、その全空間についての積分は、\(0\)ではない値をとりうるということがわかります。
したがって、この遷移は許容となります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!






