こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓

動画で使ったシートはこちら(Gibbs energy variation)
生成ギブズエネルギーと反応ギブズエネルギーの関係
まずは、標準生成ギブズエネルギー\(\Delta_\rm{f}\)\( G^\circ\)というものを導入します。
標準というのは、温度が標準温度、圧力が標準圧力の標準状態での値という意味です。
標準状態で安定に存在する単体をその元素の基準物質として、それらからある物質を生成させるときのギブズエネルギーの変化のことを指します。
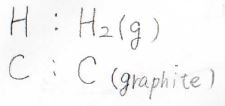
これは、標準生成エンタルピー\(\Delta_\rm{f}\)\( H^\circ\)と標準生成エントロピー\(\Delta_\rm{f}\)\( S^\circ\)を使うと、\(\Delta_\rm{f}\)\( H^\circ-T\Delta_\rm{f}\)\( S^\circ\)となります。

エンタルピー項は熱力学的な安定性、エントロピー項は分子数の変化や分子配列の変化を反映しています。
生成ギブズエネルギーの単位は\(\rm{J/mol}\)であり、その物質が\(1\ \rm{mol}\)生成するときのギブズエネルギー変化を指します。
ギブズエネルギーは状態量で、変化の経路には依存しないため、任意の反応ギブズエネルギーはいくつかの生成ギブズエネルギーの和として書くことができます。
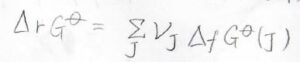
この式の中で、\(\rm{J}\)は変化に関与する化学種のいずれかを指します。
そして、\(\nu_\rm{J}\)は生成系の係数はそのまま、反応系の係数にだけ\(-1\)をかけるという化学量数です。
この標準反応ギブズエネルギーも単位は\(\rm{J/mol}\)ですが、生成ギブズエネルギーとは意味合いが違います。
こちらは、化学種\(\rm{J}\)の量が、その変化式中での係数\(\times 1\ \rm{mol}\)に対しての量となっています。
イオンの生成ギブズエネルギー
それで、化学種は分子だけではなくてイオンも含まれます。
例えば、水素分子と臭素分子が電子のやり取りをして、水素イオンと臭化物イオンが生成するということを考えましょう。
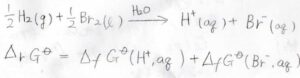
ここでは、イオンは水和しているものと考えます。
水素イオンと臭化物イオンは同時に生成するので、この反応全体のギブズエネルギー変化は、それぞれの生成ギブズエネルギーの和として書かれます。
ただ、ここで問題なのが電気的中性の原理というもので、溶液全体では、カチオンとアニオンの電荷はキャンセルされます。
つまり、アニオンとカチオンの一方だけを生成させることができません。
したがって、個別のイオンの生成ギブズエネルギーも一意的に決めることができません。
基準となる値が必要となります。
そこで慣例的に、水和した水素イオンの生成ギブズエネルギーを\(0\)とすることで、他のイオンの値も決まるようにします。
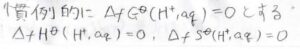
溶媒和のギブズエネルギー
イオンの熱力学的な安定性は、溶媒和の影響が大きく関わっているので、溶媒和についても考える必要があります。
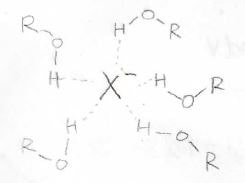
溶媒和というと、有機化学で求核置換反応の反応性の話で出てきた話でもあります。

ハロゲン化物イオンの求核性は、溶媒和の影響が大きいプロトン性溶媒中ではヨウ化物イオンが最も大きくなります。
しかし、溶媒和による安定化があまり起こらない非プロトン性溶媒中では、逆にフッ化物イオンの求核性が最も大きくなります。
詳しくは、こちらを参照してください。

この溶媒和によるギブズエネルギー変化を考えるアイデアとして、理論物理学者のマックス-ボルンは、イオンを真空中から一様な誘電体まで運ぶ際の電気的な仕事に等しいと考え、こちらのボルンの式を導きました。
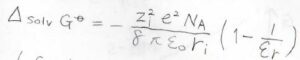
ここで、\(\varepsilon_0\)は真空の誘電率、\(\varepsilon_\rm{r}\)は溶媒の比誘電率、\(r\)はイオン半径、\(Z\)はイオンの価数、\(e\)は電気素量、\(N_\rm{A}\)はアボガドロ数です。
物理定数がいくつも入っているので、実際に数値計算する場合は、もっと簡単な式になります。
例えば、水の比誘電率\(78.54\)を代入すると、モルギブズエネルギー変化は以下のようになり、結局イオンのパラメータ2つだけあれば計算できることがわかります。
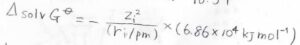
先ほどの水素イオンと臭化物イオンの生成反応について、もう一度考え直してみると、水和した水素イオンの生成ギブズエネルギーはイオン自体の生成ギブズエネルギーに溶媒和の影響を考えたものとして書けます。
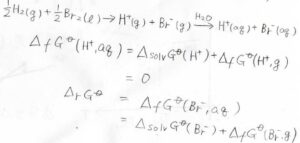
この和が慣例的には\(0\)とされます。
このとき、臭化物イオンの生成ギブズエネルギーは、反応全体のギブズエネルギー変化に等しくなります。
もちろん、溶媒和の寄与を分けて考えることもできます。
状態変化のギブズエネルギー
それでは、次に物理的な変化に伴うギブズエネルギーの変化を考えてみましょう。
熱力学第一法則とギブズエネルギーの定義より、ギブズエネルギーの微小変化\(\rm{d}\)\(G=V\rm{d}\)\(p-S\rm{d}\)\(T\)となります。

ここで、\(V\)は体積、\(p\)は圧力、\(S\)はエントロピー、\(T\)は絶対温度です。
この基本式を、\(T\)と\(p\)の二変数関数\(G\)の全微分として見ると、\(\displaystyle (\frac{\partial G}{\partial p})_T=V\)、\(\displaystyle (\frac{\partial G}{\partial T})_p=-S\)という関係が得られます。
熱力学第三法則に従う場合、エントロピーは絶対零度で\(0\)をとり、温度に対して単調増加する状態量であることから、ギブズエネルギーは温度に対して、単調減少するということになります。
エントロピーの温度依存性が小さい場合は、下のようなグラフが書けます。
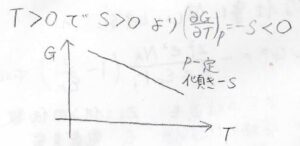
そして、固体、液体、気体という各状態で分子の配列を考えると、固体がきれいに整列しているのに対して、気体がもっとも煩雑になります。
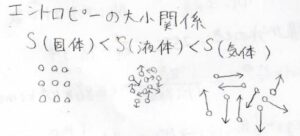
このことより、エントロピーは固体から気体に向かって大きくなっていくということになります。
これは、そのままギブズエネルギーの温度依存性に現れるので、それぞれの状態についてギブズエネルギーを図示すると、このようなグラフのようになります。
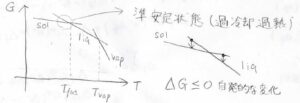
もっとも温度依存性が小さいのが固体で、もっとも大きいのが気体です。
その中間が液体です。
自発的な変化はギブズエネルギーが減少する方向へと起こるため、物質はその温度でのギブズエネルギーがより小さいほうの状態をとろうとします。
つまり、グラフ上では固体と液体の交点の温度が融点で、液体と気体の交点の温度が沸点になります。
ただ、ギブズエネルギーが高くても、その状態を保つことがあって、これを準安定状態といいます。
水を氷点下まで冷やしたのに氷にならず、衝撃を加えたら一気に氷になっていく現象は、過冷却という準安定状態がもたらすものです。
逆に融解しない、沸騰しない過熱という準安定状態もあります。
そして、ギブズエネルギーの圧力依存性は体積によって決まるわけですが、固体や液体の体積に比べると、気体の体積はとても大きいです。
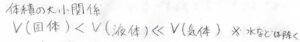
したがって、圧力を変化させたときには、気体のギブズエネルギーだけが顕著に変動することになります。
ちなみに、固体と液体は分子の密集具合は同程度で、体積にもさほど差がないので、まとめて凝集相という言い方をします。
大きな差ではありませんが、多くの物質では固体の体積が小さくなります。
ただし一部の例外として、水、単体のケイ素やビスマスなど固体の方が大きくなるものもあります。
圧力がとても小さいときには、気体のギブズエネルギーも著しく小さくなるので、下のような位置関係になります。
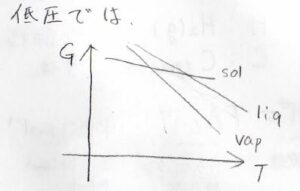
このときには、沸点が融点よりも低い温度であるようになり、実際には液体の状態が観測されないようになります。
つまり、物質は液体を経由せずに固体から気体へと変化する昇華性物質となります。
そして、もう少し高い圧力で液体の領域がちょうど現れるときには、各状態のギブズエネルギーが下のような位置関係になります。
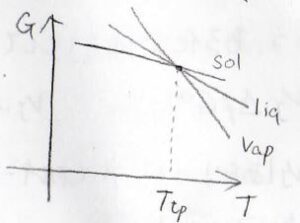
3本の線が交わるときの温度と圧力は、それぞれの物質について一意的に決まり、これが三重点となります。
横軸を温度、縦軸を圧力として書いた相図では、3本の相境界が交わって、固体と液体と気体のすべてが共存する点がこれにあたります。

気体のギブズエネルギーの圧力依存性
温度を一定として、圧力が\(p_\rm{i}\)から\(p_\rm{f}\)まで変化したとき、終点のギブズエネルギー\(G_\rm{f}\)は、始点のギブズエネルギー\(G_\rm{i}\)に\(V\rm{d}\)\(p\)の定積分を足した値として書かれます。
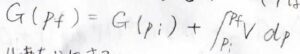
モルあたりの量にすると、下の形になります。
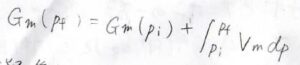
こうしておくと、体積やギブズエネルギーが物質量に比例しない示強性の量になります。
仮に、変化の前後で凝集相のままだった場合は、モル体積の変化はとても小さいと考えられるので、積分の外に出すという近似ができます。
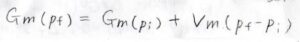
理想気体だった場合は、\(V_\rm{m}\)\(\displaystyle=\frac{RT}{p}\)なので、積分は\(\displaystyle RT\ln{(\frac{p_\rm{f}}{p_\rm{i}})}\)となります。
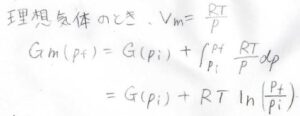
変化前の圧力\(p_\rm{i}\)を標準圧力\(p^\circ\)で置き換えると、標準ギブズエネルギーからの差を考えることもできます。
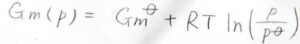
実在気体の場合には、実効の圧力\(f\)を導入することで、理想気体と同様に考えることができます。

ここで\(f\)は実際の圧力\(p\)に係数\(\phi\)をかけたものとしています。
\(f\)のことはフガシティー、\(\phi\)のことはフガシティ―係数と呼び、これは温度と圧力、物質の種類にも依存する量になります。
証明は練習問題でやりますが、圧縮率因子を\(Z\)とすると、\(\ln{\phi}\)は\(\displaystyle \frac{Z-1}{p}\)を圧力について\(0\)から\(p\)まで定積分した値となります。
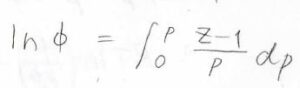
実在気体と理想気体のギブズエネルギーの圧力依存性は、下のような形になります。
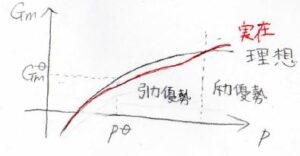
黒が理想気体で、赤が実在気体です。
定圧では分子間相互作用がはたらきにくいため、実在気体が理想気体に近いふるまいをします。
温度がボイル温度よりも低いときには、圧力が上昇するにつれて、まず引力の影響でフガシティーが下がり、実在気体のギブズエネルギーも小さくなります。
さらに圧力が上昇すると、斥力相互作用が優勢となり、今度は逆に実在気体のギブズエネルギーが大きくなることで、図のような変化の仕方をします。
練習問題
それでは最後に練習問題をやって終わります。
(1)\(-10 ^\circ\rm{C}\)において密度が\(917\ \rm{kg\ m}\)\(^{-3}\)の氷があったとして、圧力を\(1.0\ \rm{bar}\)から\(2.0\ \rm{bar}\)まで上昇させたときにモルギブズエネルギーの変化量はいくらになりますか?
(2)先ほど紹介したフガシティ―係数と圧縮率因子の関係式を導いてください。
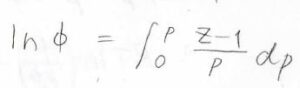
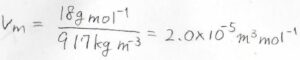
すると、\(2.0 \times 10^{-5}\ \rm{m^3\ mol^{-1}}\)となりました。
モル体積の温度依存性を無視すると、モルギブズエネルギー変化は、モル体積と圧力差の積として\(2.0\ \rm{J\ mol}\)\(^{-1}\)と計算されます。

続いて(2)では、まず実在気体について、ギブズエネルギーの圧力依存性を考えます。
圧力を\(p’\)から\(p\)まで変化させたとき、それぞれの状態のフガシティーを\(f’\)、\(f\)として、ギブズエネルギー変化は\(\displaystyle RT\ln{(\frac{f}{f’})}\)と表されます。
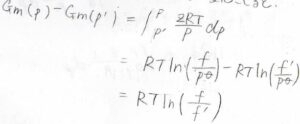
モル体積は圧縮率因子\(Z\)を使って\(\displaystyle \frac{ZRT}{p}\)と表されます。
これが理想気体であれば、こうなります。
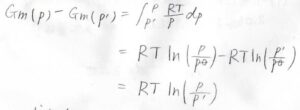
理想気体のモル体積は\(\displaystyle \frac{RT}{p}\)なので、以上の2つの式の差をとると、このような式が作れます。
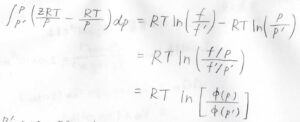
そして、対数の和をいじると、真数は\(\phi\)の比になります。
ここで、\(p’\)を\(0\)に近づけていくと、\(\phi(p’)\)は\(1\)に近づきます。
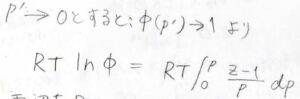
両辺についてその極限をとって、最後に両辺を\(RT\)で割ると問題にある式が出てきます。
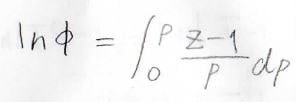
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!