こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(thermodynamics of rubber elasticity)
それでは内容に入っていきます!
ゴムの化学構造と基本的な物性
まずはゴムの基本的な話をしていきます。
ゴムとは、架橋により高分子が三次元的な網目構造を形成したものを言います。
化学結合により架橋点ができているという点で、絡み合いなど化学結合ではない架橋点形成によってできる物理ゲルとは区別されます。
ゴム状の弾性力を有する工業的材料のことは、まとめてエラストマーとも言います。
主にパラゴムノキの樹液から採れるポリイソプレンを原料に作られるゴムを天然ゴムと言って、ナフサから分離されるエチレンやスチレン、ブタジエンやイソプレンなどを原料として作られるゴムを合成ゴムと言います。
イソプレンの付加重合は、こちらの4パターンが考えられますが、よく伸びるゴムとなるのは、そのうちのポリ(シス-1,4-イソプレン)だけになります。
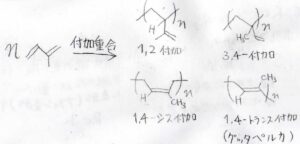
ポリ(トランス-1,4-イソプレン)からできるゴムは、ガラス転移温度が高く、室温ではまったく弾みません。
こっちのポリイソプレンは、アカテツ科の木の樹液の主成分で、グッタペルカやグッタパーチャなどと言います。
トランス型の対称性が高いことで、高分子鎖同士がより接近でき、分子運動の自由度が阻害されることが低弾性の原因です。
原理としては、多くの植物に由来するシス型の不飽和脂肪酸が常温で液体なのに対し、動物由来の飽和脂肪酸が常温で固体になるのとよく似ています。
ただ、ガラス転移は速度論的な現象で、融解は熱力学的な現象なので、明確に区別はされます。
重合の際には、Ziegler-Natta触媒などを用いることで立体規則性を制御することができます。
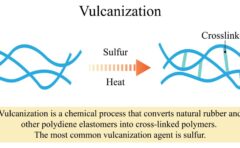
そして、硫黄分子などを付加させることで三次元網目構造を作る反応は、総称して架橋反応と言います。

特に、硫黄を使って架橋することを加硫と言います。
個々の網目鎖が自由度をもつため、熱エネルギーはそれぞれの網目鎖に等分配されます。
したがって、ゴムの張力は網目鎖の本数に比例することになります。
ゴムは、架橋されていることによる立体障害があるため、分子が整列して結晶となることができません。
つまり、ゴムには融点がありません。
それでも液体窒素などで冷却したときにはカチカチになるのですが、それはガラス転移であり、凝固ではありません。
シス型の対称性により、ガラス転移温度はきわめて低く、\(\displaystyle -70^\circ \rm{C}\)などになるため、常温では局所的なブラウン運動が液体と同程度に激しく、そのおかげで変形した瞬間に復元力がはたらきます。
しかし、化学結合により流動することができないため、ゴムは結晶ではない固体に分類されます。
ゴム弾性と熱力学量の関係
ここからは、そんなゴムの張力が熱力学的にどう表されるのかを考えていきます。
ゴムは引っ張っても、元の長さに戻るため、可逆系だと言えます。
つまり、ゴムに与えられた熱量\(\rm{d’}\)\(q\)は\(T\rm{d}\)\(S\)、体積変化を伴う仕事\(\rm{d’}\)\(w\)は\(-p\rm{d}\)\(V\)となります。
ここで、\(T\)は絶対温度、\(S\)はエントロピー、\(p\)は圧力、\(V\)はゴムの体積です。
そして、ゴムの内部エネルギーは、伸長によって与えられた仕事の寄与を考えなくてはいけないため、熱力学基本式には\(f\rm{d}\)\(L\)という項が付きます。
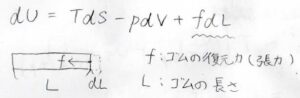
ここで、\(f\)はゴムの張力、\(L\)はゴムの長さです。
そして、長さ\(L\)と体積\(V\)は互いに独立な変数になります。
ゴムは伸長によりほとんど体積が変化しない、つまり引っ張った量に反比例して断面積が小さくなるという性質をもっているため、\(V\)を固定しても\(L\)は決まりません。
伸長による体積変化はポアソン比という量で整理されます。
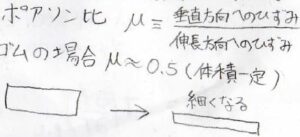
これは、伸長方向へのひずみに対して、垂直方向へのひずみがどうなるかを比として表したもので、ポアソン比が\(0.5\)というのが、体積変化しないという意味になります。
ひずみの定義については、こちらの記事でお話ししています。
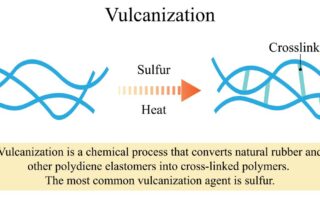
そして、熱力学基本式の項が1つ増えたということは、エンタルピー、ヘルムホルツエネルギー、ギブズエネルギーの基本式にも同じく\(f\rm{d}\)\(L\)が付くことになります。
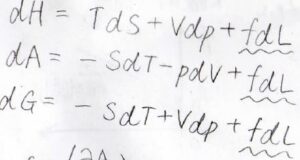
外力を与えて伸ばしたときに自由エネルギーが増大して、自発的に縮んだときに自由エネルギーが同じ分だけ減少するということになります。
これらの式を三変数関数の全微分として見ると、張力\(f\)は\(\displaystyle (\frac{\partial A}{\partial L})_{T, V}\)、つまり\(\displaystyle (\frac{\partial U}{\partial L})_{T, V}-T(\frac{\partial S}{\partial L})_{T, V}\)となります。

また、ギブズエネルギーの基本式より、\(f\)は\(\displaystyle (\frac{\partial G}{\partial L})_{T, V}\)、すなわち\(\displaystyle (\frac{\partial H}{\partial L})_{T, V}-T(\frac{\partial S}{\partial L})_{T, V}\)とも書けます。
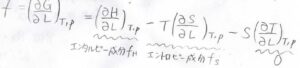
したがって、温度と体積が一定の条件下では、張力が内部エネルギー由来の成分とエントロピー由来の成分に分離できることになります。
いま、それぞれを\(f_U\)、\(f_S’\)として表すことにします。
また、温度と圧力が一定の条件下では、張力はエンタルピー由来の成分\(f_H\)とエントロピー由来の成分\(f_S\)の和として書くことができます。
ここで、マクスウェルの関係式を考えると、\(\displaystyle S=(\frac{\partial A}{\partial T})_{V, L}\)であるため、\(\displaystyle f_S’=T(\frac{\partial f}{\partial T})_{V, L}\)と書けます。

マクスウェルの関係式の考え方については、こちらを参照してください。

ただし、体積を一定として温度を変化させるというのは、熱膨張があるため、実験的には難しいです。
圧力を一定にして温度を変化させるというのは簡単なので、\(f_S’\)を求めるときには、一次の項までの近似を使うのが現実的です。

ここで、\(\lambda\)は伸長比と言って、ゴムの長さ\(L\)を自然長\(L_0\)で割った値です。
\(\alpha_T\)は線膨張率で、一般的なゴム材料では\(2.2 \times 10^{-4}\ \rm{K}\)\(^{-1}\)程度になることが知られています。
この値を知らなかったとしても、この線膨張率の決定は実験的に難しくありません。
そして、圧力と長さを固定して、横軸\(T\)、縦軸\(f\)としてプロットすれば、その温度における傾きから\(f_S\)を求めることができます。
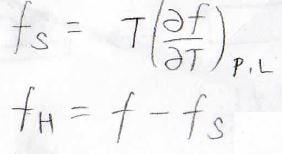
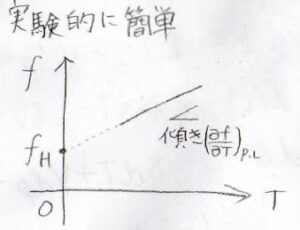
またこのとき、一定の傾きの直線を引くと、縦軸の切片が\(f_H\)になります。
ここで注意しておきたいのは、このようなプロットはあまり文献には載せない、ということです。
それは、\(f\)が試料の大きさに依存してしまうためです。

そこで、張力を断面積で割った応力\(\sigma\)を使うことで、ゴムの内部情報だけを取り出すのが一般的です。
応力の単位は\(\rm{Pa}\)になりますが、これは圧力というより、単位体積あたりのエネルギー\((\rm{J\ m}\)\(^{-3}\))として見たほうが、ゴムの内部情報としてのイメージを捉えやすいと思います。
ゴム弾性の分子論的起源
最後に、エンタルピー成分とエントロピー成分の分子論的な起源について考えて終わります。
エンタルピー成分の起源は、結合角や結合長のひずみです。
これを伸びきりとも言います。


結合性軌道のポテンシャルの谷はとてもシャープなので、結合長が少し変化しただけでも大きな復元力が生じます。
対して、エントロピー成分はもっと大きなスケールの構造変化に起因しています。
ボルツマンの式より、エントロピーはとりうる微視的状態の数\(W\)が大きいほど大きな値となります。
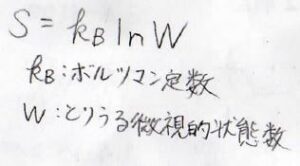
ボルツマンの式の導出過程は、こちらを参照してください。

いま、\(1\)本の網目鎖に着目したとすると、架橋点間の直線距離\(R_\rm{c}\)が小さいときには、鎖の経路がいろいろとれることがわかります。

対して、\(R_\rm{c}\)がほとんど経路長と等しくなったときには、どのような経路をとるのかという場合の数が少なくなります。
つまり、試料全体の巨視的な変形量に比例して網目鎖の局所的な変形量も決まる場合には、ゴムを引っ張るほどエントロピーは減少することになります。
このような変形のことをアフィン変形と言います。
伸長による体積変化がないとした場合、エントロピーと伸長比の関係は、下のように表されます。
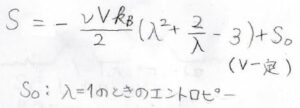
ここで\(\nu\)は単位体積あたりの網目鎖の本数、つまり数密度で、\(S_0\)は自然長のときのエントロピーです。
導出については、こちらを参照してください。

一次元的には、ゴムは長さが\(0\)になるまで縮もうとするはずですが、三次元的に考えると、それでは垂直方向へのひずみがとても大きくなってしまって、全体のエントロピーは小さくなってしまいます。
そのため、ゴムは\(0\)ではない自然長をもちます。
以上のことを踏まえて全体の張力\(f\)は長さ\(L\)に対して、このような逆S字型の変化をします。
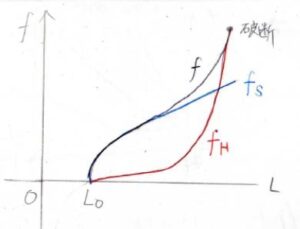
変形量が小さいときには、網目鎖全体の構造変化により復元力が発現するため、エントロピー成分が大きく寄与します。
この領域では、エンタルピー成分は張力全体の\(1\)~\(2\)割程度しかありません。
金属やセラミックスでは、分子が小さいためここまでエントロピーが寄与することはありません。
そして、誰しも経験上わかると思いますが、ゴムは引っ張りすぎるとちぎれます。
ちぎれることは破断とも言いますが、その直前は網目鎖の経路長以上に伸びることを強いられるため、結合長や結合角にひずみが生じます。
その結果、エンタルピー成分が優勢となり、一気に張力が跳ね上がります。
縦軸を応力、横軸をひずみとしたグラフでも似たような形になりますが、それはstrainとstressの頭文字をとって、ssカーブという呼び方をします。
破断に至るまでに試料に与えられた仕事は、こちらの斜線部の面積に等しく、これを破断エネルギー、タフネスなどと呼びます。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!