こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはエントロピーに関して、ボルツマンの式の導出です。
始めに、ボルツマンの式を紹介したのち、統計の理論をもとに導出していきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(Boltzmann equation)
僕のプロフィールはこんな感じになってますので、よろしくお願いします。
それでは内容に入っていきます！
ボルツマンの式とは？
まずはじめに、ボルツマンの式とはどんなものかお話します。
エントロピーを\(S\)、ボルツマン定数を\(k_\rm{B}\)\(\)とすると、\(S=k_\rm{B}\)\(\ln{W}\)という関係が成り立ちます。
この式がボルツマンの式です。
ここで、\(W\)はとりうる微視的状態の数です。
つまり、離散的なエネルギー準位をもつ粒子がどのように分布するのかという場合の数になります。
ここからの導出で詳しくお話しするので、ここでは、ふーんと思ってもらったら十分です。
そして、↓の熱力学的なエントロピーの定義に対して、ボルツマンの式は統計的な定義であるといわれます。
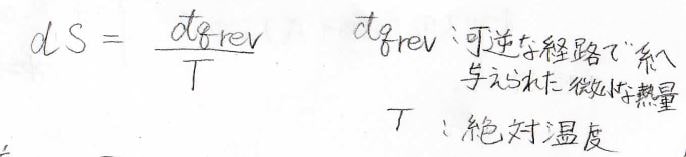
ボルツマンの式導出
じゃあ、ここから実際にこの式を導出していきます。
まず、ここからは簡単のためにとある気体分子が\(N\)個閉じ込められているという系を考えていきます。
分子がもつエネルギーは不連続な値となるとして、それぞれのエネルギーの値を低いものから\(\varepsilon_0\)、\(\varepsilon_1\)と数えることにします。
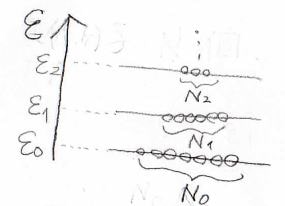
また、それぞれのエネルギー準位にある分子の個数を\(N_0\)、\(N_1\)とします。
このとき、気体の内部エネルギーは、それぞれの分子がもつエネルギーの総和であるため、\(\sum_i N_i \varepsilon_i\)と書けます。
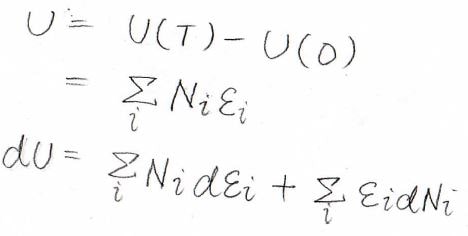
そして、その微小変化\(\rm{d}\)\(U\)は、全微分として書けます。
それぞれの項の意味を言葉で説明すると、次のようになります。
まず第一項は、各状態の分子数はそのままで、エネルギーに変化が起こったときの内部エネルギー変化を指します。
井戸型ポテンシャルから考察すると、この寄与は井戸の横幅が大きくなることと対応しています。
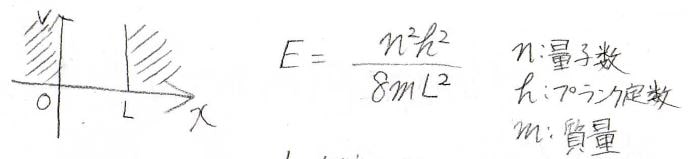
三次元であれば体積の変化に関係していることになりますから、第一項は系がされた仕事\(\rm{d’}\)\(w\)に相当します。
井戸型ポテンシャルについてはこちらを参照ください。
そして、第二項は各状態のエネルギーはそのままで分子数が変化することによる内部エネルギーの変化を指します。
ボルツマン分布の式より、これは単純に分子の熱運動が加速されたことと対応していますので、これが系に与えられた熱量\(\rm{d’}\)\(q\)に相当します。
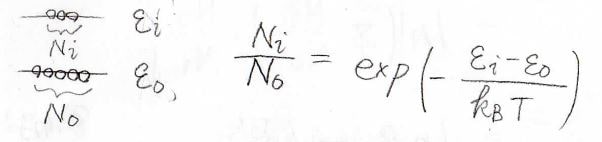
したがって、熱力学的なエントロピーの定義より、エントロピーの微小変化\(\rm{d}\)\(S\)は、このように書けます。
ここで\(T\)の逆数については、ボルツマン分布の式を導出したときに出てきた\(\beta\)を使って、\(k_B \beta\)と書き換えることができます。
詳しくは、こちらの記事を参照してください。
それで、とりうる微視的状態の数\(W\)は、高校でも習った通り、階乗を使ってこのように書けます。
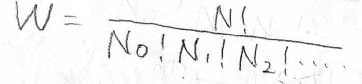
その対数をとって、こちらのスターリングの近似を使います。
すると、\(\sum_i N_i\)は\(N\)ですからキャンセルされて、\(N \ln{N}-\sum_i (N_i \ln{N_i})\)となります。
これをある特定の\(N_i\)について偏微分すると、\(\ln{N}-\ln{N_i}\)、すなわち\(\ln{(N/N_i)}\)となります。
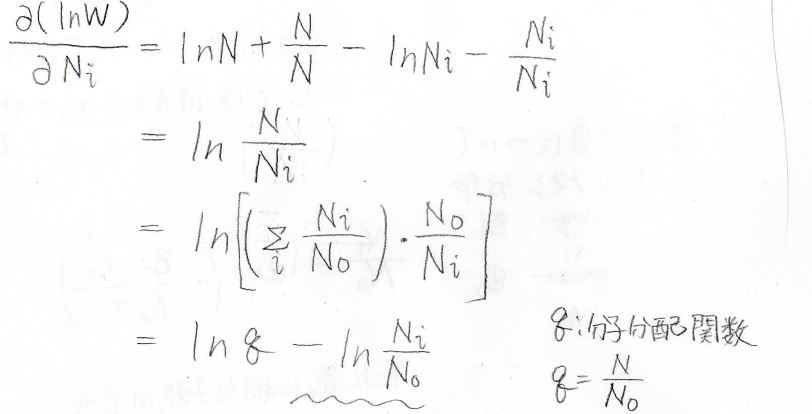
そして、基底状態の分子数を\(N_0\)として、\(N/N_0\)は、分子分配関数\(q\)と書けますので、\(\ln{(N/N_i)}=\ln{q}-\ln{(N_0/N_i)}\)となります。
ここで、ボルツマン分布の式より、\(-\ln{(N_0/N_i)}=\beta (\varepsilon_i-\varepsilon_0)\)となります。
したがって、エントロピーの微小変化\(\rm{d}\)\(S\)はこのように書けます。
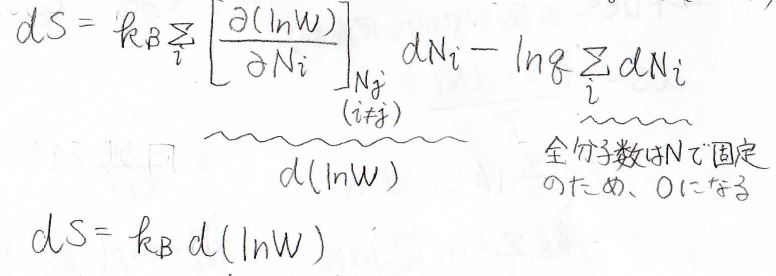
すると、第二項の部分は\(\ln{q}\)が定数なので\(\sum\)の外に出せて、\(\ln{q} \sum_i \rm{d}\)\(N_i\)となります。
ここでは、密封された気体を考えているので、全体の分子数の和に変化はなく、\(\sum_i \rm{d}\)\(N_i=0\)となります。
そして、第一項は、\((\frac{\partial (\ln{W})}{\partial N_i})\rm{d}\)\(N_i\)の部分が全微分の形となっているので、結局\(\rm{d}\)\(S=k_\rm{B}\)\( \rm{d}\)\((\ln{W})\)となります。
両辺を\(0\ \rm{K}\)\(\)から\(T\)までの温度について定積分すると、\(S=k_\rm{B}\)\(\ln{[W(T)]}-k_\rm{B}\)\(\ln{[W(0\ \rm{K})]}\)となります。
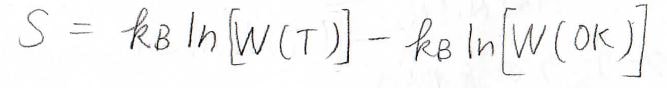
これが統計のみによって導かれるエントロピーの式です。
そして、以降の記事でまた詳しくやりますが、\(0\ \rm{K}\)\(\)におけるボルツマン分布は、すべての分子が基底状態になっているはずなので、\(N=N_0\)より\(W=1\)となります。
したがって、\(0\ \rm{K}\)\(\)におけるエントロピーは\(0\)となることが予想されます。
したがって、少なくとも固体や気体などの状態変化を考えない今回の場合は、\(S=k_\rm{B}\)\(\ln{W}\)というボルツマンの式が成り立つことになります。
\(0\ \rm{K}\)\(\)におけるエントロピーについては、熱力学第三法則についての記事でもっと詳しく扱っていきます！
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
コメント