こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(phase boundary)
それでは内容に入っていきます!
化学ポテンシャル
まず、化学ポテンシャルについて改めてお話しします。
単成分系に限らず一般的な系において、成分\(i\)の化学ポテンシャルをこのように定義します。
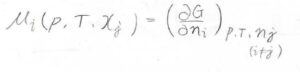
全体のギブズエネルギー\(G\)を圧力\(p\)と絶対温度\(T\)、そして成分\(i\)以外のすべての物質量を固定したまま、成分\(i\)の物質量\(n_i\)について微分します。
この式の中で\(x_j\)は、成分\(j\)のモル分率を指します。
組成が同じでも、全体の物質量を大きくすれば、ギブズエネルギーはそれに比例して大きくなっていきますが、化学ポテンシャルは変化しません。
単成分系のときには、ギブズエネルギーを物質量について偏微分する操作は、ギブズエネルギーを物質量で割る操作と同じなので、化学ポテンシャルはモルギブズエネルギー\(G_\rm{m}\)と等しくなります。
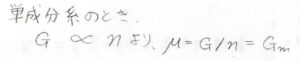
仮に、\(\beta\)相から\(\alpha\)相へ、物質が微小量\(\rm{d}\)\(n\)だけ輸送されたとき、ギブズエネルギーの変化は\(\mu(\alpha)\rm{d}\)\(n-\mu(\beta)\rm{d}\)\(n\)となります。

これが平衡状態のときには、ギブズエネルギー一定となるので、\(\mu(\alpha)=\mu(\beta)\)となります。

このように、平衡状態を扱うためには、全体のギブズエネルギーではなく、化学ポテンシャルを使うことになります。
クラペイロンの式
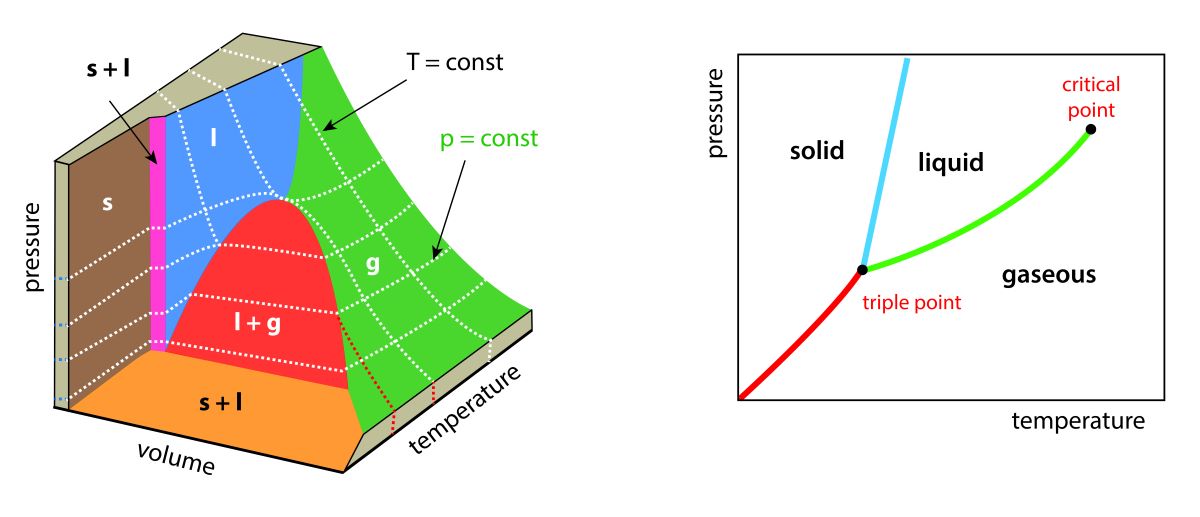
ではここから、単成分系について、相境界における圧力と温度の関係を考えていきましょう。
単成分系なので、化学ポテンシャルはモルギブズエネルギーと同じです。
熱力学基本式を使うと、\(\displaystyle (\frac{\partial \mu}{\partial T})_p=-S_\rm{m}\)、\(\displaystyle (\frac{\partial \mu}{\partial p})_p=V_\rm{m}\)となります。
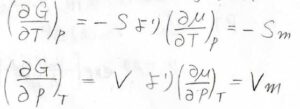
ここで、\(S_\rm{m}\)はモルエントロピー、\(V_\rm{m}\)はモル体積で、どちらも正の値をとります。
ここから、横軸を温度、縦軸を圧力として書いた相図の中で、相境界の傾き\(\displaystyle \frac{\rm{d}\mathit{p}}{\rm{d}\mathit{T}}\)を求めていきます。
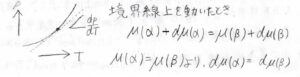
平衡状態を保ちながら温度が変化していったとき、その温度変化によって変化した化学ポテンシャルを\(\rm{d}\)\(\mu\)として、\(\mu(\alpha)+\rm{d}\)\(\mu(\alpha)=\mu(\beta)+\rm{d}\)\(\mu(\beta)\)となります。
もちろん、温度変化する前でも平衡状態だったため、\(\mu(\alpha)=\mu(\beta)\)となります。
したがって、変化量\(\rm{d}\)\(\mu\)についても等しくなります。
そして、全微分の式を使うと、\(-S_\rm{m}\)\((\alpha)\rm{d}\)\(T+V_\rm{m}\)\((\alpha)\rm{d}\)\(p=-S_\rm{m}\)\((\beta)\rm{d}\)\(T+V_\rm{m}\)\(\rm{d}\)\(p\)という関係が導かれます。
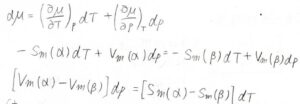
相転移によるモル体積の変化を\(\Delta_\rm{trs}\)\(V\)、モルエントロピーの変化を\(\Delta_\rm{trs}\)\(S\)として整理すると、\(\displaystyle \frac{\rm{d}\mathit{p}}{\rm{d}\mathit{T}}=\frac{\Delta_\rm{trs}\mathit{S}}{\Delta_\rm{trs}\mathit{V}}\)という式が出てきます。
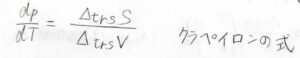
この式をクラペイロンの式と呼びます。
この式より、相境界において温度の関数となっている圧力の傾きは、相転移によるエントロピー変化と体積変化によって決まるということになります。
また、相転移によるモルエンタルピーの変化を\(\Delta_\rm{trs}\)\( H\)とすれば、\(\Delta_\rm{trs}\)\(\displaystyle S=\frac{\Delta_\rm{trs}\mathit{H}}{T_\rm{trs}}\)となるため、クラペイロンの式は、\(\displaystyle \frac{\rm{d}\mathit{p}}{\rm{d}\mathit{T}}=\frac{\Delta_\rm{trs} \mathit{H}}{T\Delta_\rm{trs} \mathit{V}}\)という形で書くこともできます。

固-液相境界
それでは、実際に固相と液相の相境界について、圧力と温度の関係を考えてみましょう。
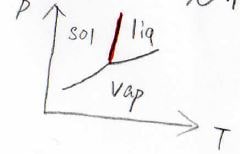
\(\displaystyle \frac{\Delta_\rm{trs}\mathit{H}}{\Delta_\rm{trs}V}\)の温度依存性が無視できるときには、クラペイロンの式の両辺に\(\rm{d}\)\(T\)をかけて、左辺を圧力の式、右辺を温度の式という形にすることができます。

実際、固相と液相は凝集相と呼ばれており、分子間距離が温度によって大きく変化するわけではないので、どちらの熱膨張率もさほど大きくありません。
温度を\(T^\ast\)から\(T\)まで変化させたとして両辺を定積分すると、\(\displaystyle p=p^\ast+\frac{\Delta_\rm{fus}\mathit{H}}{\Delta_\rm{fus}\mathit{V}}\ln{(\frac{T}{T^\ast})}\)となります。

さらに、\(T\)と\(T^\ast\)の差が小さいとすると、\(\ln{(1+x)}=x\)の近似を使って、\(\displaystyle p=p^\ast+\frac{\Delta_\rm{fus}H}{T^\ast\Delta_\rm{fus}V}(T-T^\ast)\)という一次関数が出てきます。
つまり、固相と液相の相境界は、直線に近い形をとるという予想ができます。
気-液相境界
それで、次に気相と液相の相境界について考えてみます。
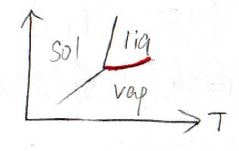
気体については、理想気体として扱えるものだと仮定します。
すると、理想気体の状態方程式より、気体のモル体積は\(\displaystyle \frac{RT}{p}\)と書くことができます。

ここで\(R\)は気体定数です。
さらに、液体のモル体積は気体に比べてとても小さいため、\(\displaystyle \frac{RT}{p}\)がほぼ体積変化と等しいと考えることができます。

クラペイロンの式に、この近似を使うと、\(\displaystyle \frac{\rm{d}\mathit{p}}{\rm{d}\mathit{T}}=\frac{p\Delta_\rm{vap}\mathit{H}}{RT^2}\)となります。
この式をクラウジウス-クラペイロンの式と呼びます。
両辺に\(\displaystyle \frac{\rm{d}\mathit{T}}{p}\)をかけると、左辺が圧力、右辺が温度の式の形に分離できるので、先ほどと同じように積分すると、\(\displaystyle p=p^\ast \exp{[-\frac{\Delta_\rm{vap} \mathit{H}}{R}(\frac{1}{T}-\frac{1}{T^\ast})]}\)という式が得られます。

これをグラフにすると、下のような変曲点をもちうる関数となります。

温度の範囲は、左端が三重点の温度で、右端が臨界温度です。
固-気相境界
最後に、固相と気相の相境界について考えてみます。
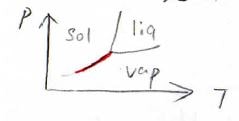
式の形は、液相と気相の相境界とまったく同じですが、転移エンタルピーの大きさが異なります。
そして、エンタルピーは状態量でありため、その変化量は変化の経路に依存しません。
したがって、固体から一気に気体になった場合と、固体から液体を経由して気体になった場合でまったく同じ値になるはずです。
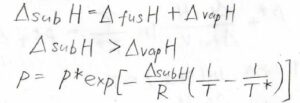
これを利用すると、昇華エンタルピーは蒸発エンタルピーよりも融解エンタルピーの分だけ大きいことになります。
これはつまり、三重点付近で曲線の傾きを比較したときに、その傾きは必ず固相と気相の相境界のほうが大きくなるというです。
相図の概形
以上のことを踏まえて、気体が理想気体となる場合の相図を書くと、このようになります。
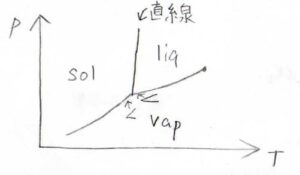
まず、多くの物質で固体よりも液体の方がモル体積が大きいので、固体と液体の相境界となる直線の傾きの符号は正になります。
水や単体のビスマスなど、固体の方がモル体積が大きいときには、この傾きが負になります。
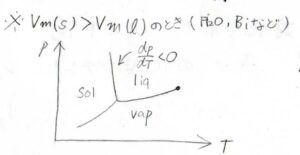
そして、三重点付近での傾きは、蒸気圧曲線よりも固相と気相の相境界のほうが大きくなります。
別の不活性ガスが封入してあるとき
少し特殊な例として、次の系も考えてみます。
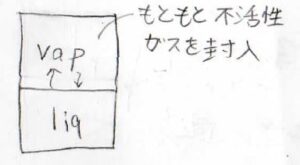
容器の中に液体と気体が共存しているのですが、あらかじめ別の不活性ガスを封入しておくことで、気相だけが混合物となっている系です。
液体が存在しているため、不活性ガスではない方の気体の分圧は、飽和蒸気圧となります。
液相だけが、不活性ガスの存在により加圧されているというイメージです。
温度一定とすると、化学ポテンシャルの微小変化\(\rm{d}\)\(\mu=V_\rm{m}\)\(\rm{d}\)\(p\)と書けます。
平衡状態では液相と気相の値が等しくなるため、下の等式が書けます。

この式の中で、\(\rm{d}\)\(p\)は蒸気圧の微小変化で、\(\rm{d}\)\(P\)は不活性ガスの存在により全圧が大きくなった分を指しています。
不活性ガスがないときの蒸気圧を\(p^\ast\)とすると、今の蒸気圧\(p\)は下の積分によって求められます。
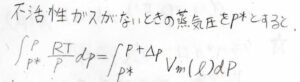
液体のモル体積の圧力依存性を無視し、さらに蒸気圧の変化はとても小さいものだとしたときには、\(\displaystyle p=p^\ast\exp{[\frac{V_\rm{m}(\rm{l})\mathit{\Delta P}}{RT}]}\)となります。
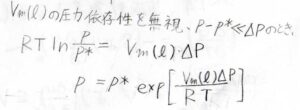
実際、液体のモル体積は気体に比べてとても小さいため、蒸気圧の変化は全圧の変化よりきわめて小さくなります。
以上のように別の気体があった場合は、少しだけ蒸気圧曲線が上に動きます。
練習問題
それでは最後に、練習問題をやって終わります。
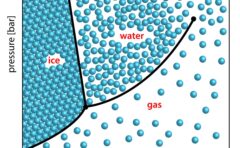
(1)氷の上を滑るスケートの問題です。
水の固相と液相の相境界の傾きは負であるため、人が氷の上に立つと、融点は下がります。
それにより接地部分で液体の層ができて、滑ることができます。
では、その融点の変化が何度になるかを求めてください。
スケート靴片足分の接地面積は\(7.5\ \rm{cm}\)\(^2\)、重力加速度は\(9.8\ \rm{m\ s}\)\(^{-2}\)、融解エントロピーは\(22\ \rm{J}\)\(\ \rm{K}\)\(^{-1}\ \rm{mol}\)\(^{-1}\)、モル体積変化は\(-1.6\ \rm{cm}\)\(^3\ \rm{mol}\)\(^{-1}\)であるとします。
ただし、これらの状態量変化の圧力依存性は無視できるものとします。
(2)水蒸気が理想気体として考えられ、水の蒸発エンタルピーが\(40.7\ \rm{kJ}\)\(\ \rm{mol}\)\(^{-1}\)、臨界温度が\(6.47 \times 10^2\ \rm{K}\)だったときに、水の蒸気圧曲線は変曲点をもつかどうかを判定してください。
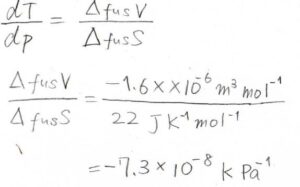
人が氷に乗ったときにかかる圧力の増加分を\(\Delta p\)とすると、それはこのような式で\(3.3 \times 10^5\ \rm{Pa}\)となります。

体重は両足に分散されるので、\(2\)で割っていることに注意してください。
最後にこれらをかけると、融点の変化は\(-2.4 \times 10^{-2}\ \rm{K}\)と計算されます。

そして(2)、変曲点の温度は\(\displaystyle \frac{\Delta_\rm{vap} \mathit{H}}{2R}\)で求められますが、これは\(2.45 \times 10^3\ \rm{K}\)、つまり数千度のとても高温のところになります。
蒸気圧曲線の右端である臨界点の温度が\(6.47 \times 10^2\ \rm{K}\)であるため、\(3\)倍程度の差があります。

位置関係をグラフにすると、下のようになります。
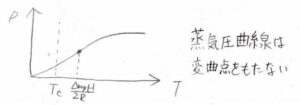
右端である臨界温度よりもさらに右側に変曲点があることになるため、実際の蒸気圧曲線には変曲点は現れないことになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!