それではどうもありがとうございました!
こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(heterogeneously catalyzed reaction)
それでは内容に入っていきます!
1分子反応
始めに、不均一触媒によって、1つの分子が2つに分解するという反応を考えます。

ポテンシャル図は、こちらのようになります。
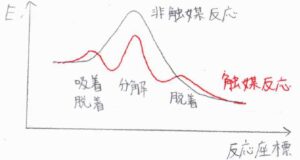
吸着して分解した後に脱着するというように、複数の素反応が組み合わさって、一連の触媒反応は起こります。
分解の過程が律速段階であるとき、分解が起こると速やかに最後の脱着が進行します。
被覆率を\(\theta\)、分解の素反応の速度定数を\(k_\rm{r}\)\(\)とすると、全体の反応速度\(v\)は、\(k_\rm{r}\)\(\theta\)と書けます。
もし、分解前の分子の吸着と脱着が平衡状態にあるとすれば、吸着等温式によって、分解速度を圧力の関数として書くことができます。
\(\theta\)がラングミュアの等温式で書けるとき、\(v=k_\rm{r}\)\(\frac{\alpha p}{1+\alpha p}\)となります。
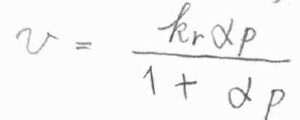
ここで\(\alpha\)は、分解前の分子の吸着および脱着の速度定数の比です。
2分子反応
ここからは、2分子反応について、2つの機構を考えていきます。
助触媒と触媒毒
その前に、少し補足をします。
まず、2種類以上の化学種が競合して、同じ固体表面に吸着することは、共吸着といいます。
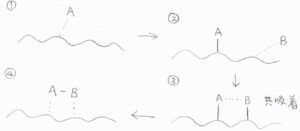
一般的に、第1の吸着質が吸着したときに、固体表面で電子構造の変化が起こるため、第2の吸着質の吸着速度は、その影響を受けます。
触媒のはたらきを増強する物質のことは助触媒、阻害する物質のことは触媒毒といいます。
これからお話しする2分子反応の例では、その効果は考えられていないので、そのことに留意してください。
ラングミュア-ヒンシェルウッド(LH)機構
表面に吸着した2種類の化学種\(\rm{A}\)\(\)と\(\rm{B}\)\(\)の間で反応が進行して、生成物\(\rm{P}\)\(\)ができるというものです。
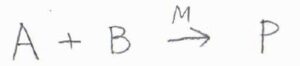
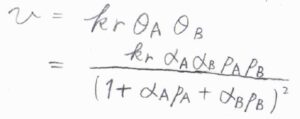
\(\rm{P}\)\(\)の生成速度\(v\)は、\(\rm{A}\)\(\)が占める吸着点の割合\(\theta_\rm{A}\)\(\)と\(\rm{B}\)\(\)が占める吸着点の割合\(\theta_\rm{B}\)\(\)の両方に比例します。
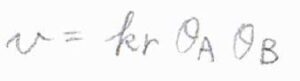
ここで、\(\theta_\rm{A}\)\(\)と\(\theta_\rm{B}\)\(\)について、ラングミュアの等温式と同じ仮定をします。
すると、\(\rm{A}\)\(\)の吸着速度は\(k_\rm{a, A}\)\(p_\rm{A}\)\(N_\rm{sites}\)\((1-\theta_\rm{A}\)\(-\theta_\rm{B}\)\()\)、\(\rm{A}\)\(\)の脱着速度は\(k_\rm{d, A}\)\(N_\rm{sites}\)\( \theta_\rm{A}\)\(\)、\(\rm{B}\)\(\)の吸着速度は\(k_\rm{a, B}\)\(p_\rm{B}\)\(N_\rm{sites}\)\((1-\theta_\rm{A}\)\(-\theta_\rm{B}\)\()\)、\(\rm{B}\)\(\)の脱着速度は\(k_\rm{d, B}\)\(N_\rm{sites}\)\(\theta_\rm{B}\)\(\)と書けます。
ここで、\(p_\rm{A}\)\(\)と\(p_\rm{B}\)\(\)はそれぞれの分圧、\(N_\rm{sites}\)\(\)は固体表面にある吸着点の総数です。
\(\frac{k_\rm{a, A}}{k_\rm{d, A}}\)\(\)を\(\alpha_\rm{A}\)\(\)、\(\frac{k_\rm{a, B}}{k_\rm{d, B}}\)\(\)を\(\alpha_\rm{B}\)\(\)とすると、平衡状態で\(\alpha_\rm{A}\)\(p_\rm{A}\)\((1-\theta_\rm{A}\)\(-\theta_\rm{B}\)\()=\theta_\rm{A}\)\(\)、\(\alpha_\rm{B}\)\(p_\rm{B}\)\((1-\theta_\rm{A}\)\(-\theta_\rm{B}\)\()=\theta_\rm{B}\)\(\)という連立方程式が得られます。
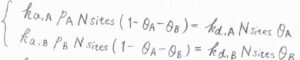
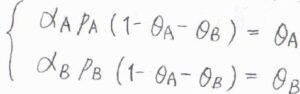
これを解くと、\(\theta_\rm{A}\)\(=\frac{\alpha_\rm{A}\mathit{p}_\rm{A}}{1+\alpha_\rm{A}\mathit{p}_\rm{A}+\alpha_\rm{B}\mathit{p}_\rm{B}}\)、\(\theta_\rm{B}\)\(=\frac{\alpha_\rm{B}\mathit{p}_\rm{B}}{1+\alpha_\rm{A}\mathit{p}_\rm{A}+\alpha_\rm{B}\mathit{p}_\rm{B}}\)となります。
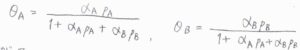
したがって、全体の反応速度\(v\)は、\(k_\rm{r}\)\(\frac{\alpha_\rm{A}\alpha_\rm{B}\mathit{p}_\rm{A}\mathit{p}_\rm{B}}{(1+\alpha_\rm{A}\mathit{p}_\rm{A}+\alpha_\rm{B}\mathit{p}_\rm{B})^2}\)と求められます。
イーレイ-リディール(ER)機構
先ほどのLH機構と異なり、2種類の化学種のうち、吸着するのは一方のみです。
気体である\(\rm{B}\)\(\)がすでに吸着している\(\rm{A}\)\(\)と衝突することで、\(\rm{P}\)\(\)ができるという機構です。
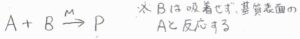
反応速度は、\(\rm{A}\)\(\)の被覆率\(\theta_\rm{A}\)\(\)と\(\rm{B}\)\(\)の分圧\(p_\rm{B}\)\(\)に比例します。
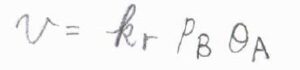
\(\theta_\rm{A}\)\(\)がラングミュアの等温式で書けるとき、\(v=k_\rm{r}\)\(\frac{\alpha p_\rm{A}\mathit{p}_\rm{B}}{1+\alpha p_\rm{A}}\)\(\)となります。
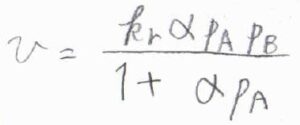
\(\alpha p_\rm{A}\)\(\)がとても大きいとき、\(v\approx k_\rm{r}\)\(p_\rm{B}\)\(\)となり、律速段階は吸着している\(\rm{A}\)\(\)と気体の\(\rm{B}\)\(\)との衝突となります。
\(\alpha p_\rm{A}\)\(\)がとても小さいときには\(v\approx k_\rm{r}\)\(\alpha p_\rm{A}\)\(p_\rm{B}\)\(\)と、反応速度が\(\alpha\)に依存することになります。
実際の不均一触媒反応の機構
最後に、ここで紹介したLH機構とER機構は、あくまで理想的な極限です。
現実に起こるすべての反応は、両者の間のどこかに位置しており、それぞれの機構の特徴を示すことになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!



