こんにちは!
それでは今回も化学のお話やっていきます。
今日はテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(harmonic oscillator calculus of variations)
ではまいります!
計算条件
まず、計算条件を考えていきます。
まず、調和振動子のポテンシャルはばね定数を\(k\)として\(\frac{1}{2}kx^2\)になるのでハミルトニアンはこの形になります。
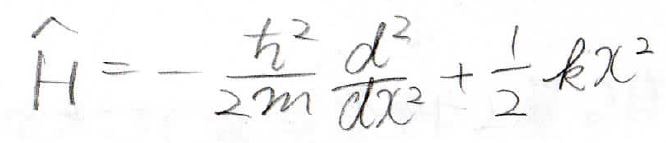
それで、今回は基底状態と第一励起状態の2つについて試行関数を考えます。
\(x\)が無限大の時の極限からこのような予測が立てられます。
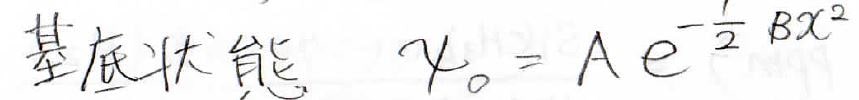
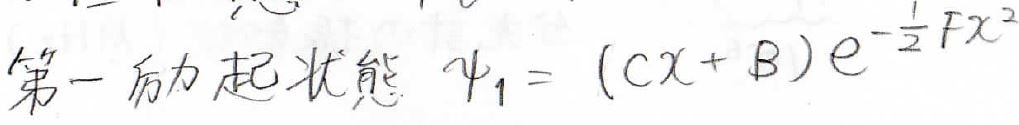
ここに関しては調和振動子を変分法を使わずに解く記事がありますので、こちらをご覧ください。

それで、各状態間での直交性が成り立つようにこの積分は\(0\)になるとします。
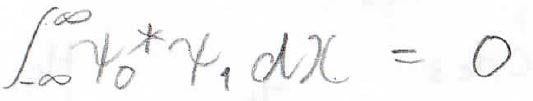
エネルギーは前回同様にこの式で与えられます。
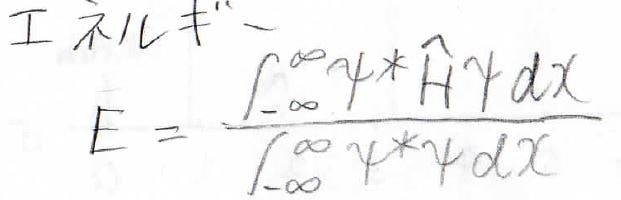
前回の記事はこちらです。
変分法を使って水素原子の基底状態について考えています。

基底状態
では実際に変分法を使ってエネルギーを求めてみましょう。
始めに基底状態についてみていきます。
規格化
規格化の式を考えると、まず、このような式が得られます。
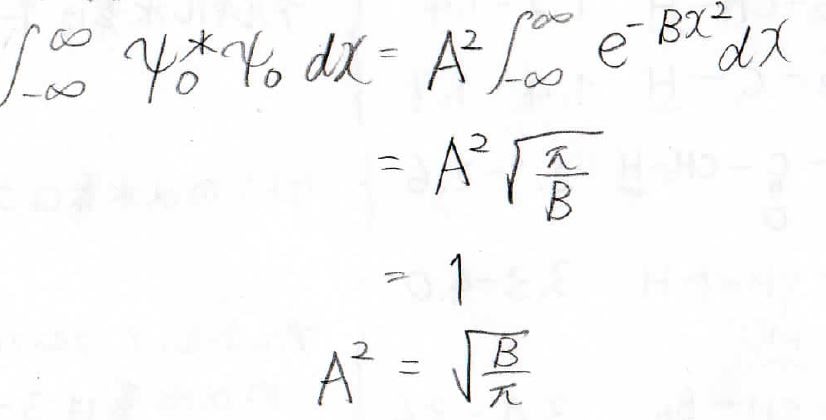
この積分はガウス積分と呼ばれる形になっていて、その値は\sqrt{\frac{\pi}{B}}になります。
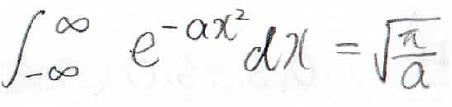
結果、\(A^2\)は\(\sqrt{\frac{B}{\pi}}\)で与えられるということがわかりました。
エネルギー
続いて基底状態のエネルギーを求めてみます。
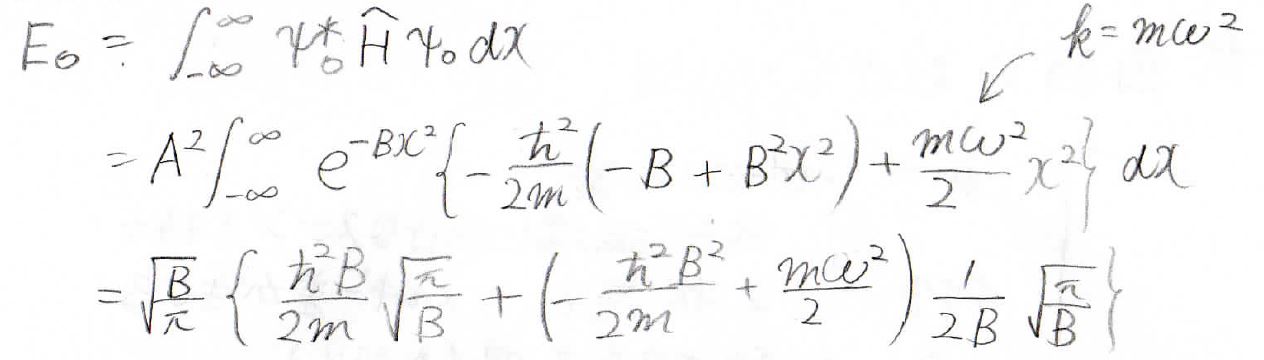
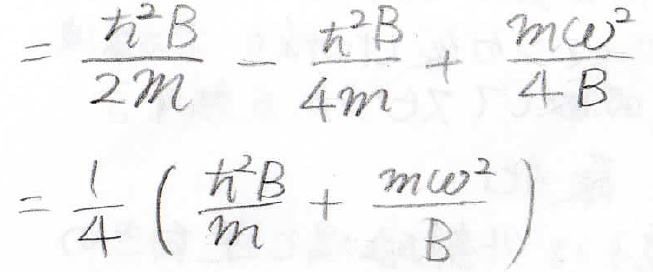
\(x^2\exp{(-Bx^2)}\)の積分もガウス積分の公式から値が分かるので、結局、これがエネルギーの値となります。
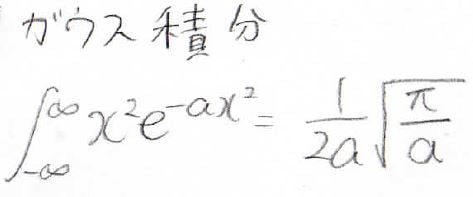
エネルギーの極小
続いて、このエネルギーの極小を求めるために未知数である\(B\)でエネルギーを微分すると、このような関係が得られました。
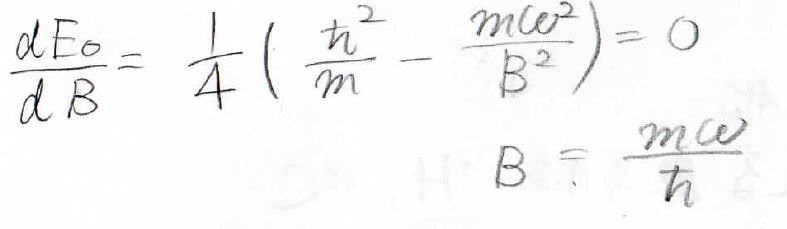
これより、\(B\)は\(\frac{m\omega}{\hbar}\)というのが求められました。
最後にこれをエネルギーの式に代入することでエネルギーの極小値を求めます。
すると\(\frac{1}{2}\hbar \omega\)というのが答えになります。
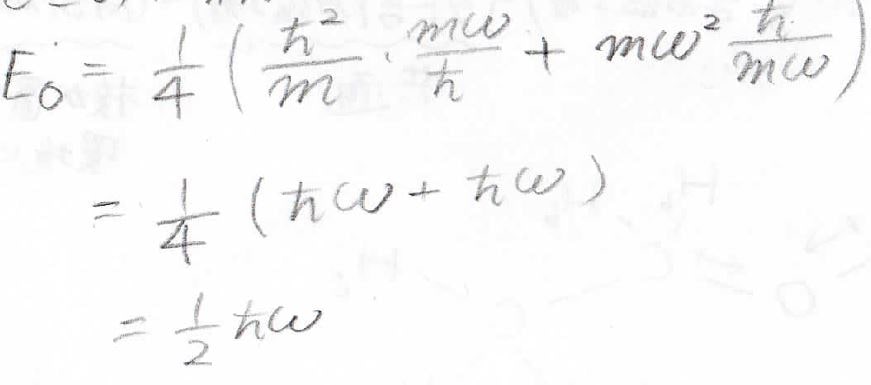
第一励起状態
はい、基底状態についてのエネルギーがわかったので、続いては第一励起状態のエネルギーを考えます。
直交性
まずは基底状態との間の直交性を満たすように考えると、この第二項が奇関数を\(-\infty\)から\(\infty\)まで積分しているものなので、\(0\)になり、第一項だけが残ってきます。
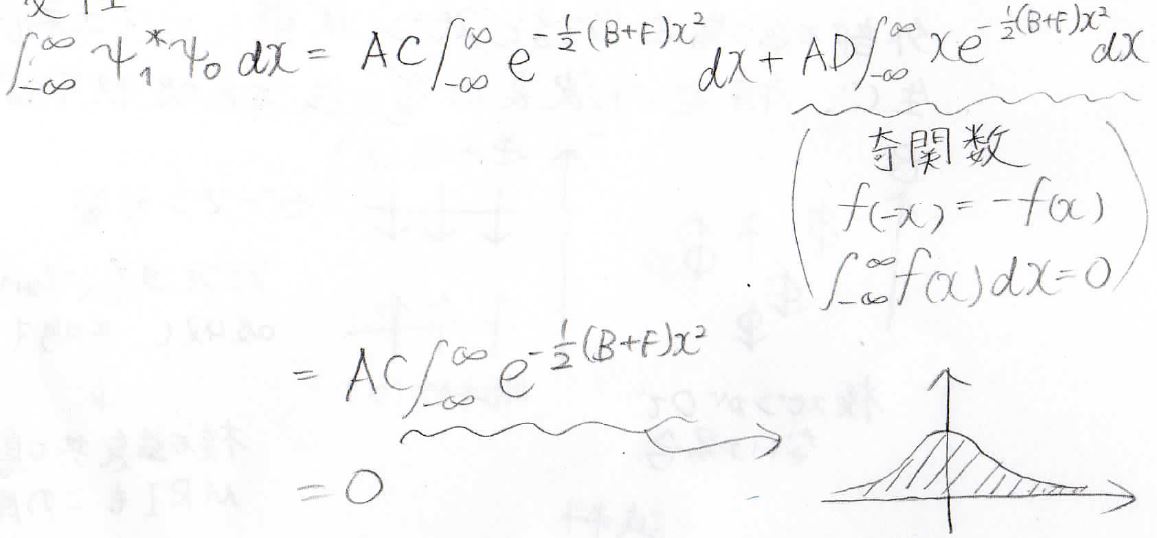
この積分は常に\(0\)より大きい関数の積分なので、\(0\)にはなりません。
そして\(A\)は基底状態の計算より、\(0\)にはならないことが分かっています。
したがってこれが\(0\)になるためには\(C\)が\(0\)になるしかないことになります。
その結果、第一励起状態の波動関数はこの形で与えられるということが分かります。
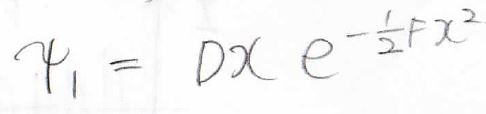
規格化
これを規格化すると、先ほど紹介したガウス積分の公式を使って、\(D^2\)が\(2F\sqrt{\frac{\pi}{F}}\)となります。
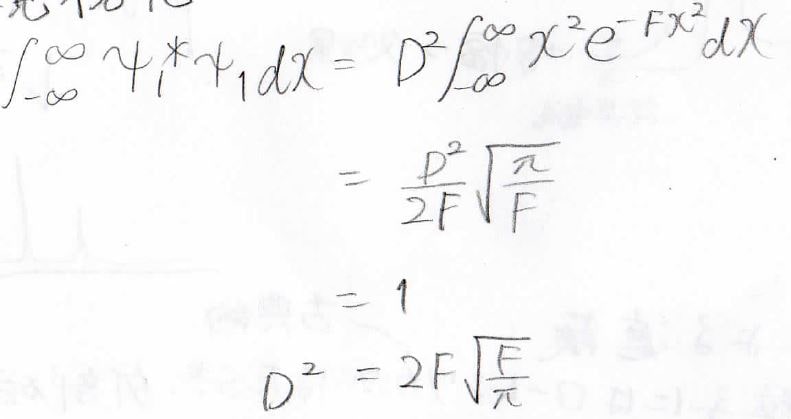
エネルギー
これを踏まえてエネルギーを考えると、このような式が得られます。
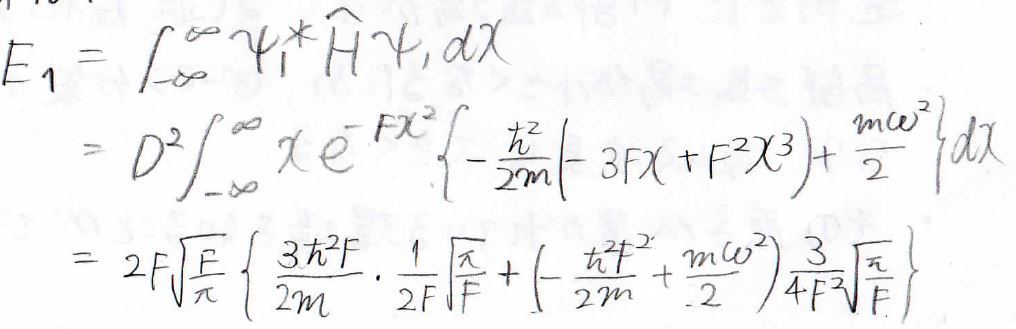
ここで\(x^4\exp{(-Fx^2)}\)の積分には、ガウス積分の公式を使っています。
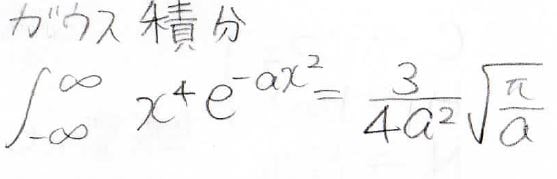
エネルギーをさらに変形していくと、結局この形になります。
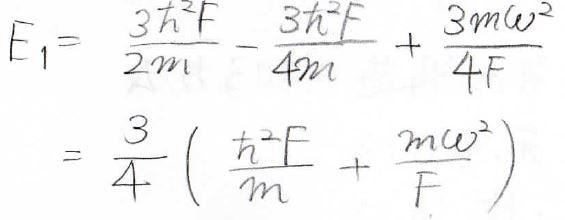
エネルギーの極小
では同じようにこれを微分して極小を求めていきます。
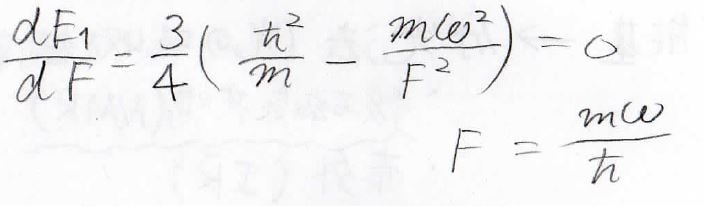
導関数が\(0\)になることを利用すると\(F\)は\(B\)と同じく\(\frac{m\omega}{\hbar}\)となり、これを代入することで、第一励起状態のエネルギーは\(\frac{3}{2}\hbar \omega\)と出てきました。
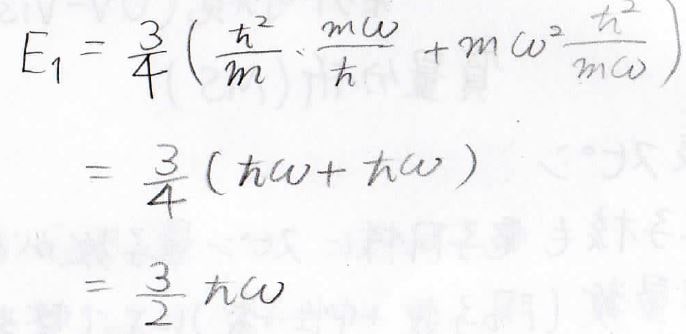
変分法を使っていない場合との比較
変分法によって導かれたエネルギーは、基底状態で\(\frac{1}{2}\hbar \omega\)、第一励起状態で\(\frac{3}{2}\hbar \omega\)となりました。
これは、シュレディンガー方程式から変分法を使わずに求められたエネルギー準位の式\(E_n=(n+\frac{1}{2})\hbar \omega\)と矛盾しておらず、確かに同じ答えを得ることができました。
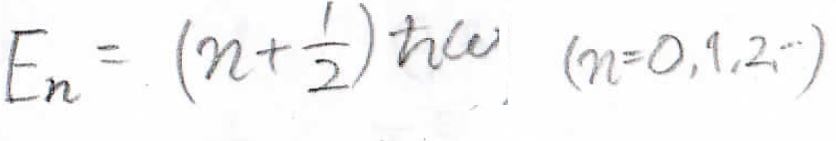
調和振動子のシュレディンガー方程式については、こちらを参照してください。
今回はやりませんが、第二励起状態以降も同様の計算によって求められるので、お時間ある方はぜひ試してみてください。
まとめ
それでは練習問題はありませんので、最後軽くおさらいをやって終わります。
今回は変分法を使って調和振動子のエネルギーを求めてみました。
調和振動子の計算はそのままやると、エルミート多項式が出てきて結構難しいのですが、変分法なら高校生でもできる計算によってエネルギーを計算することができます。
その際に必要になるのはガウス積分の公式くらいです。
複数の状態を考える場合は、その状態間での直交性を利用することで、うまく計算することができます。
それではどうもありがとうございました!