こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(colligative properties)
それでは内容に入っていきます!
束一的性質とは?
まず、言葉の説明からやっていきます。
束一的とは、その化学種が何であるかに関係なくあてはまるという意味です。
特に溶液系においては、溶質の化学種に依存しない性質のことを指して、束一的性質と言います。
例えば、理想希薄溶液について、溶媒についてラウールの法則が成り立つわけですが、これは溶質が何であるかに関係なく、ただ何かが溶解しているという理由だけで現れる性質です。

対して、溶質について成り立つヘンリーの法則では、比例定数\(K_\rm{B}\)が溶質と溶媒の両方に依存するので、これは束一的性質ではありません。
そして、高校で習う沸点上昇や凝固点降下、浸透圧といった現象も、ただ何かが溶けているというだけで現れている現象なので、束一的性質の例となります。
沸点上昇
それでは、それぞれの現象について、溶液の組成がどのように影響を及ぼすのか、近似を使いながら式を作っていきます。
まず、計算条件として、次のような系を考えます。
2成分\(\rm{A}\)と\(\rm{B}\)の混合溶液において、\(\rm{A}\)を溶媒、\(\rm{B}\)を溶質と呼ぶことにします。
\(\rm{A}\)のモル分率\(x_\rm{A}\)は\(1\)に近く、ラウールの法則が成り立ちます。
また、\(\rm{B}\)は不揮発性であり、気相は純粋な\(\rm{A}\)しか存在しないと考えてよいものとします。
平衡状態では、液相の化学ポテンシャル\(\mu_\rm{A}\)\((\rm{l}\)\()=\mu_\rm{A}\)\(^\ast(\rm{l}\)\()+RT\ln{x_\rm{A}}\)となり、これが純粋な気相の化学ポテンシャル\(\mu_\rm{A}\)\(^\ast(\rm{g}\)\()\)と等しくなります。
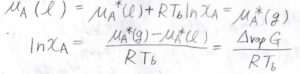
\(\mu^\ast\)は純粋なときの化学ポテンシャル、\(R\)は気体定数、\(T_\rm{b}\)は沸点です。
これを整理すると、\(\displaystyle \ln{x_\rm{A}}=\frac{\mu_\rm{A}^\ast(\rm{g})-\mu_\rm{A}^\ast(\rm{l})}{RT_\rm{b}}\)となります。
さらに、純粋なときの化学ポテンシャルはモルギブズエネルギーと等しいため、\(\mu_\rm{A}\)\(^\ast(\rm{g}\)\()-\mu_\rm{A}\)\(^\ast(\rm{l})\)は蒸発ギブズエネルギー\(\Delta_\rm{vap}\)\( G\)と書き換えることができます。
ここからさらに変形していくために、少し前に紹介したギブズ-ヘルムホルツの式を使います。
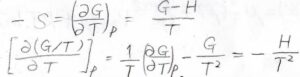
熱力学基本式より、エントロピーを\(S\)とすると、\(\displaystyle (\frac{\partial G}{\partial T})_p=-S\)となります。
また、ギブズエネルギーの定義より、\(\displaystyle -S=\frac{G-H}{T}\)とも書けます。
\(\displaystyle [\frac{\partial (G/T)}{\partial T}]_p=\frac{1}{T}(\frac{\partial G}{\partial T})_p-\frac{G}{T^2}\)となりますが、\(\displaystyle (\frac{\partial G}{\partial T})_p=\frac{G-H}{T}\)なので、\(\displaystyle [\frac{\partial (G/T)}{\partial T}]_p=-\frac{H}{T^2}\)という関係式が導かれます。
これがギブズ-ヘルムホルツの式です。
これをもとに、圧力一定として、\(\ln{x_\rm{A}}\)を温度について偏微分すると、\(\displaystyle -\frac{\Delta_\rm{vap} \mathit{H}}{RT_\rm{b}^2}\)となります。

さらに、両辺に\(\rm{d}\)\(T\)をかけて定積分します。
積分の範囲は、純粋な溶媒のときから、溶質が溶けて溶液となるときまでです。
蒸発エンタルピー\(\Delta_\rm{vap}\)\( H\)の温度依存性を無視すると、左辺はそのまま\(\ln{x_\rm{A}}\)となり、右辺は\(\displaystyle \frac{\Delta_\rm{vap} \mathit{H}}{R}(\frac{1}{T_\rm{b}}-\frac{1}{T_\rm{b}^\ast})\)となります。
ここで、\(T_\rm{b}\)\(^\ast\)は純粋な\(\rm{A}\)の沸点です。
さらに、溶質\(\rm{B}\)のモル分率\(x_\rm{B}\)は\(1\)よりも十分に小さいと考えられるときには、\(\ln{(1-x)}\)が\(-x\)と近似できることを利用して、左辺を\(-x_\rm{B}\)と書き換えることができます。
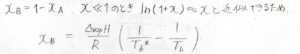
そして多くの場合、沸点の上昇値は、絶対温度としての沸点の値よりも小さいため、\(T_\rm{b}\)\(^\ast T_\rm{b}\)\(=(T_\rm{b}\)\(^\ast)^2\)と考えてもよいことにします。
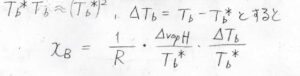
すると、\(x_\rm{B}\)\(\displaystyle =\frac{1}{R}\frac{\Delta_\rm{vap} \mathit{H}}{T_\rm{b}^\ast}\frac{T_\rm{b}-\mathit{T}_\rm{b}^\ast}{T_\rm{b}^\ast}\)となります。
\(\displaystyle \frac{\Delta_\rm{vap} \mathit{H}}{T_\rm{b}^\ast}\)は、純粋な\(\rm{A}\)の蒸発に伴うエントロピー変化に対応し、トルートンの規則より、多くの物質について、経験的に\(85\ \rm{kJ\ K^{-1}\ mol^{-1}}\)くらいになることが知られています。
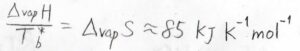
これも定数として考えれば、沸点の上昇値\(\Delta T_\rm{b}\)\(\displaystyle =R\frac{T_\rm{b}^\ast}{\Delta_\rm{vap} \mathit{H}}T_\rm{b}\)\(^\ast x_\rm{B}\)となります。
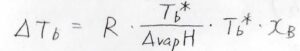
つまり、沸点の上昇値は溶質のモル分率に比例し、その比例定数は純粋な溶媒の沸点によってだいたい決まるということです。

ただし、水やメタンの蒸発エントロピーは、トル―トンの規則から外れるので、注意が必要です。
実験的には、モル分率よりも扱いやすい質量モル濃度\(b\)を使って、その比例定数\(K_b\)を決定することが多いです。

凝固点降下
続いて、凝固点降下についても考えてみましょう。
先ほどと同様に、溶媒についてラウールの法則が成り立つものとします。
また、固相には溶質は存在しないものとします。
平衡状態では、液相における溶媒の化学ポテンシャル\(\mu_\rm{A}\)\((\rm{l}\)\()\)が純粋な固相の化学ポテンシャル\(\mu_\rm{A}\)\(^\ast (\rm{s}\)\()\)と等しくなります。

先ほどと同じような近似を使って変形すると、\(x_\rm{B}\)\(\displaystyle =\frac{\Delta_\rm{fus} \mathit{H}}{R}\frac{\Delta T_\rm{m}}{(T_\rm{m}^\ast)^2}\)となります。
ここで、\(\Delta_\rm{fus}\)\( H\)は融解エンタルピー、\(\Delta T_\rm{m}\)は凝固点の降下した値を正とした量です。
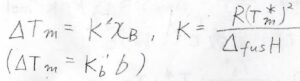
この関係より、やはり凝固点降下でも、凝固点の変化は溶質の濃度に比例するという結論になります。
凝固点降下法
理論上、この比例定数をあらかじめ決定しておけば、濃度未知の溶液の濃度を決定することも可能です。
このような方法を凝固点降下法と言います。
ただし、この式が溶媒についてラウールの法則が成り立つことを前提としているため、適用可能な濃度域が狭く、現在はほとんど行われていません。
他の濃度決定方法としては、滴定や吸光度測定などがあり、これらの方がよく用いられています。
溶解度(非束一的性質)
それで、実は、凝固点降下とほぼ同じ式で溶解度の温度依存性も式を立てることができます。
ただし、溶解度は溶質の化学種によって変化するため、束一的性質ではありません。
ここでは、先ほどと異なり、固相は純粋な溶質であるモデルを考えます。
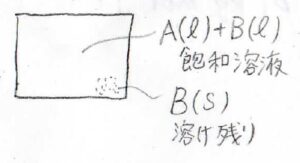
そして、溶質についてラウールの法則が成り立つことを仮定します。
すると平衡状態では、それぞれの相で\(\displaystyle \rm{B}\)の化学ポテンシャルが等しくなることから、\(\ln{x_\rm{B}}\)\(\displaystyle =\frac{\Delta_\rm{fus} \mathit{G}}{RT}\)という関係が導かれます。

ここで、\(\Delta_\rm{fus}\)\( G\)は融解ギブズエネルギーですが、溶媒ではなく溶質の値になります。
さらに、ギブズ-ヘルムホルツの式を使うと、このように変形できます。
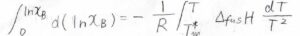
結局、\(x_\rm{B}\)\(\displaystyle =\exp{[\frac{\Delta_\rm{fus}\mathit{H}}{R}(\frac{1}{T}-\frac{1}{\mathit{T}_\rm{m}^\ast})]}\)となります。
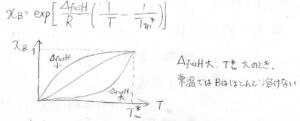
融解エンタルピーが小さいほど、低い温度でも溶解度が高くなります。
反対に、融解エンタルピーが大きく、純粋なときの融点が高い溶質ほど、溶けにくいことになります。
ただし、ここでは理想溶液を考えているため、溶媒の化学種の物質定数が入っていません。
実際には溶媒と溶質の組み合わせによって、溶解度が変わりますので、そこに注意してください。
浸透圧
最後、浸透圧についても考えてみます。
まず、浸透圧の定義からお話しします。
半透膜で区切られたU字管の一方に純粋な溶媒、そしてもう一方に溶液を入れると、エントロピーを大きくするために溶媒分子が溶液の方へ流れ込むという現象が起こります。
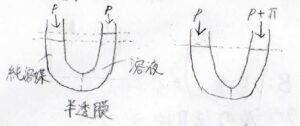
その結果、液面の高さに差が生じます。
この液面の高さが同じになるためには、溶液の方にだけ余計な圧力を印加する必要があります。
そのために必要な圧力を浸透圧\(\Pi\)と呼びます。
平衡状態では、大気圧pにおける純粋な溶媒の化学ポテンシャル\(\mu_\rm{A}\)\(^\ast(p)\)は、圧力\(p+\Pi\)の溶液における\(\rm{A}\)の化学ポテンシャル\(\mu_\rm{A}\)\((x_\rm{A}\)\(,p+\Pi)\)と等しくなります。
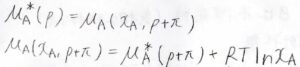
ラウールの法則が成り立つことを仮定すると、\(\mu_\rm{A}\)\((x_\rm{A}\)\(,p+\Pi)=\mu_\rm{A}\)\(^\ast(p+\Pi)+RT\ln{x_\rm{A}}\)となります。
さらに、純粋なときの化学ポテンシャルはモルギブズエネルギーと等しいため、熱力学基本式から圧力依存性がわかります。
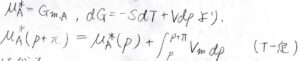
\(\rm{d}\)\(G=-S\rm{d}\)\(T+V\rm{d}\)\(p\)より、温度が一定のとき、\(\displaystyle \int_{p}^{p+\Pi}V_\rm{m}\)\(\rm{d}\)\(p\)が化学ポテンシャルの差になります。
したがって、\(\displaystyle \mu_A^\ast(p)=\mu_A^\ast(p)+\int_{p}^{p+\Pi}V_\rm{m}\)\(\rm{d}\)\(p+RT\ln{x_\rm{A}}\)となります。
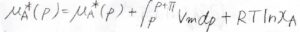
両辺に\(\mu_\rm{A}\)\(^\ast(p)\)があるので、キャンセルできます。
さらに、浸透圧は大気圧に比べて十分に小さく、モル体積\(V_\rm{m}\)の圧力依存性は無視できるものとします。
\(\ln{x_\rm{A}}\)を\(-x_\rm{B}\)と近似して整理すると、\(x_\rm{B}\)\(RT=\Pi V_\rm{m}\)となります。
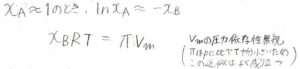
さらに、溶質の体積を無視して、両辺に全物質量\(n\)をかけると、\(n_\rm{B}\)\(RT=\Pi V\)となります。
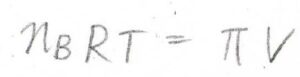
これを\(\Piに\)ついて整理すると、\(\Pi=[\rm{B}\)\(]RT\)となり、ファントホッフの式が導かれます。
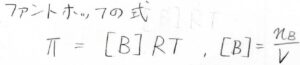
ただし、\([\rm{B}]\)は溶質のモル濃度を指します。
溶質が低分子であれば、低濃度域でこの関係がある程度成り立ちます。
浸透圧ビリアル展開
ただし、溶質が高分子になると、この関係は成り立ちません。
そこで、このようにビリアル展開の形で考えることが一般的です。
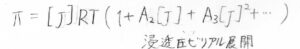
変数を質量濃度\(c\)とした場合は、このように書くこともできます。

この式を2次の項までで考えることにすると、横軸を\(c\)、縦軸を\(\Pi/c\)として一次関数が書けます。
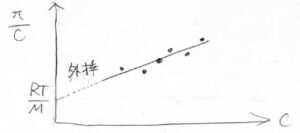
データをプロットしていき、その近似直線を濃度\(0\)まで外挿すると、その切片は\(RT/M\)となります。
\(M\)は、溶質の分子量です。
これを利用すると、浸透圧の濃度依存性から高分子の分子量を決定することができます。
分子間相互作用を反映した第二ビリアル係数も、グラフの傾きから求められます。
これを浸透圧法と言います。
一般的な合成高分子試料の分子量は単分散ではなく分布をもつため、ここで求められた分子量は平均の値になります。
数平均、重量平均、Z平均など、平均のとり方はいくつかあるのですが、浸透圧のように束一的性質を利用して得られる分子量は、数平均分子量となります。
ただし、分子量が大きいほどグラフの切片が小さくなり、精度が出ないという欠点があるため、現在は光散乱法の方がよく用いられています。
これには、光検出器の技術発展が大きく寄与しています。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




