こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(Gibbs phase law)
それでは内容に入っていきます！
相とは？
まず、相とは何かという話からしていきます。
相とは、その中では組成や物理状態が均一となるような物質の形態を指します。
例えば、固体の相は固相、液体の相は液相、気体の相は気相と言います。
そして固相は、分子配列や結合様式の違いから、さらに複数の種類に分類される物質がいくつもあります。
例えば、硫黄は低い温度で斜方硫黄ですが、温度を上げることで、単斜硫黄となり、体積が膨張、結晶の形も変化します。
斜方硫黄は\(\alpha\)相、単斜硫黄は\(\beta\)相と言います。
さらに温度を上げると、これも単斜硫黄ではあるのですが、別の\(\gamma\)相に転移します。
異なる物質だと、単体のスズにも複数の固相があります。
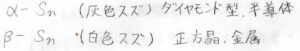
金属の性質をもっているスズは正方晶型の結晶構造をもっていて、白色スズと呼ばれています。
それを冷却していくと、ダイヤモンド型の結晶構造となり、半導体の物性を示すようになります。
金属光沢を失ったこのスズは灰色スズと言います。
白色スズを冷却することで、相転移とともに体積が大きくなることで、機械的な破壊が起こるのですが、この現象はスズペストと呼ばれます。
YouTubeの中で、動画もあったので貼っておきます。
伝播するように破壊が起こるのが伝染病のようだということで、スズのペストと言われています。
また、水にはもっとたくさんの種類の固相があることが知られています。
状態量や分率といったパラメータを軸にとったグラフ上で、どの相になるのかを表したものを相図と言いますが、水の相図はこんな感じになります。
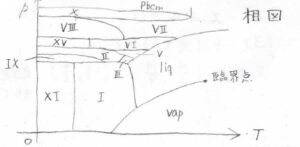
liqというのが液相で、vapが気相を指します。
I相というのが、日常で目にする一般的な氷です。
この相図より、周りの環境次第では、\(100^\circ \rm{C}\)\(\)を超える氷も存在することになります。
相と層の違い
ここで、少し言葉の整理をしたいと思います。
化学の分野では、「相」の字でソウという場合と、「層」の字でソウという場合があります。
英語では、それぞれphaseとlayerという全く別の単語として区別されます。
phaseの意味は、冒頭でもお話した通り、その中で組成や物理状態が均一となる物質の形態であり、layerの意味は、厚みをもつ構造体です。
例えば、分液ロートを使っていたときに、密度の違いで下側に水溶液、上側に有機溶媒の溶液というふうに分離したとします。
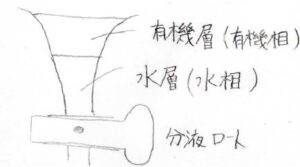
このとき、layerの字を使って下側を水層、上側を有機層というふうに呼びます。
ただ、ここで下側を水相、上側を有機相と書いても、間違いとは言い切れません。
このlayerの中では、組成が均一となっているからです。
日本語では音が同じなので、紛らわしいのですが、こんなふうにどちらでも意味が通ってしまうことも多いです。
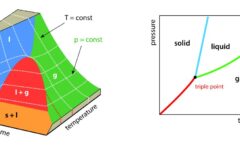
ただ、下のイメージのように、固相から固相への相転移の途中、微結晶が点在しているような状態では、層の字は使いません。
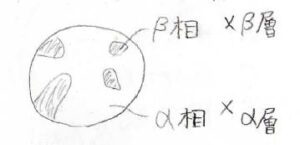
相とガラスの違い
そしてもう1つ、このphaseと明確に区別されるものとして、ガラス状態があります。
ガラスといえば、二酸化ケイ素などを主成分とした硬く透明ななの物質を思い浮かべる人が多いと思いますが、ガラスという言葉にはもう1つ意味があります。
それは、ケイ酸化合物に限らず、非結晶のまま固まってしまったものを指します。
アモルファスとほとんど同じ意味だと思えば結構です。
物質が結晶となるためには、バラバラだった分子配列がきれいに整列する必要があります。
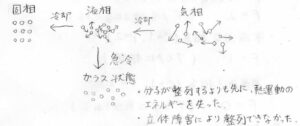
ですが、分子の拡散よりも早いスピードで冷却すると、整列するよりも前に、分子の位置を変える熱エネルギーを失い、バラバラの分子配列ののまま、カチカチになってしまいます。
ガラス状態とは、こんな状態のことを指します。
線状高分子の多くは、完全に並べたくても、絡まったコードみたいになっているので、完全に結晶となることができず、結晶とガラスの混ざった状態になります。
また、ゴムや低密度ポリエチレンに代表されるように、立体障害によりそもそも結晶化できない高分子もたくさんありますが、この場合でも冷却すればガラスにはなるので、見た目は固体になります。
そして、ケイ酸化合物のガラスは無秩序に化学結合を形成することで、ガラスになります。
完全なガラスは結晶格子を持たないため、光の干渉が起こらず、高い透明性をもちます。
一部が結晶化していると、白く濁ってきます。
熱い飲み物も入れられる耐熱性ペットボトルは、一部を結晶化させることでガラス転移温度以上でも骨格を維持できるように処理したものです。
結晶化している証拠に、飲み口の部分が真っ白になっています。
それで、流体がガラス化することは相転移とは呼ばず、ガラス転移と呼びます。
この2つは、全く異なる現象です。
まず相転移は、孤立系としてのエントロピーを最大化するために起こります。
つまりは熱力学的な現象であり、平衡状態を保ちながら相転移が起こります。
対して、ガラス転移は冷却の速さと分子運動の激しさ、この2つのバランスで決まります。
つまり、速度論的な現象になります。
相転移のようで相転移とは異なる現象ということで、擬相転移と言われることもあります。
ガラス状態であっても、分子の熱運動は完全に停止しているわけではなく、何千年、何万年といった時間のスケールでゆっくり結晶になっていく過程が止まって見えているものなので、ガラスは過冷却などのような非平衡状態だと言えます。
温度や圧力だけではなく、冷却速度などによっても状態が変化するため、相図の中にガラス状態を書くことはできません。
高分子やケイ酸化合物以外でも、単体だと硫黄やヒ素、無機物だと二酸化ケイ素、酸化ホウ素もガラス化させやすい物質として知られています。
また、水も条件次第でガラス化させることが可能で、ガラスでは分子配列が液体のままなので、体積膨張が起こりません。
この技術を利用すれば、水を多く含む生体試料を破壊することなく活動を止めることができます。
本来、タンパク質の構造解析では、x線の散乱強度を確保するために結晶化させなくてはならず、結晶化する条件を探すのがとても大変だったわけですが、水をガラス化させて電子線を当てれば、その必要がなくなるので非常に強力です。
電子線によってたんぱく質が損傷するなどのデメリットもあるのですが、気になる方は一度「クライオ電子顕微鏡」で調べてみてください。
あと、混合物ですがチョコレートもガラス状態です。
水と油のように互いに混ざり合わない物質が乳化した状態で冷やし固められたもので、結晶ではありません。
チョコレートを少しだけ温めてからもう一度冷やすと、一部が白くなることがありますが、これは熱運動が加速されたことで、平衡状態へと近づき、油分が分離することで起こります。
この現象はブルーミングと呼ばれています。
ギブズの相律
相とガラスの違いの話はこれで一区切りとして、ここからはギブズの相律というものの話をしていきます。
ギブズの相律は、共存する相の数と可変度、すなわち独立なパラメータの数の関係を表したルールです。
式は、\(F=C-P+2\)で与えられます。
\(F\)が可変度、\(C\)が成分の数、\(P\)が相の数です。
純物質の場合は、\(C=1\)なので、\(F=3-P\)という式になります。
\(2\)成分の混合物では、\(F=4-P\)となります。
単成分かつ\(1\)相系であるときには、\(F=2\)になります。
これは例えば温度と圧力という2つのパラメータに着目すると、それぞれが独立して自由に変化するということです。
対して、単成分\(2\)相系では\(F=1\)になります。
この場合、1つしか独立なパラメータがないということなので、温度によって圧力が決まることになります。
そして、単成分3相系では\(F=0\)ですから、自由に変化するパラメータはない、つまりある決まった値に固定されることになります。
このことは、相図で説明した方がわかりやすいです。
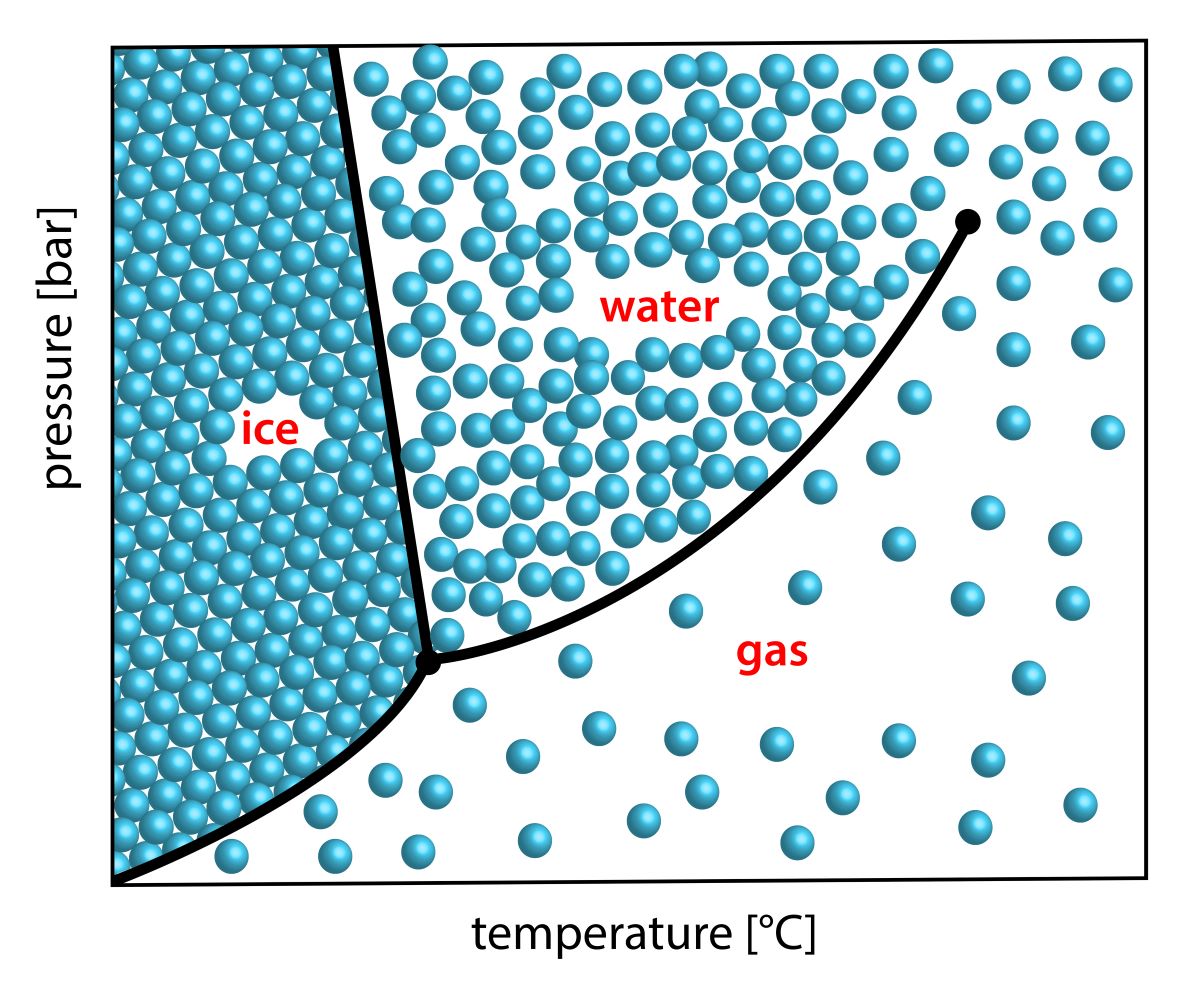
横軸を温度、縦軸を圧力として、水の相図を書くと、こんな形になります。
\(1\)相系というのは、この図の中で、sol、liq、vapと書かれたところになります。
2つのパラメータが自由に変化できるという部分は、グラフ平面上で面積をもった領域として現れます。
そして\(2\)相系は、\(p=f(T)\)という関数になるので、グラフ上では線になります。
この線のことを相境界と言います。
3相系は、温度と圧力が固定されるので、グラフ上で点になります。
これが三重点です。
そして、\(4\)相系以上はこのグラフ上に書くことはできず、そんな状態にはなりえないということも、ギブズの相律は言っています。
導出のあらまし
最後に、このギブズの相律がどのような理屈で出てきたのかというのを、高校の数学を使って簡単に考えて、終わりにしたいと思います。
まず、その準備として化学ポテンシャルという状態量を定義します。
単成分系に限らず一般的に考えるときには、物質量に比例してしまう示量性のギブズエネルギーではなく、物質量に比例しない示強性の量を使って、平衡などの議論をします。
成分iの化学ポテンシャルを\(\mu_i\)とすると、それはこちらの式で定義されます。
系全体のギブズエネルギーを温度と圧力、そして成分\(i\)以外のすべての成分の物質量を固定した状態で、成分\(i\)の物質量について微分するというものです。
これは、温度と圧力の二変数関数となります。
また、単成分系では、単純に物質量に比例するギブズエネルギーを物質量で割るのと同じですから、化学ポテンシャルはモルギブズエネルギー\(G_\rm{m}\)\(\)になります。
それで、\(\alpha\)相と\(\beta\)相という\(2\)相が共存しているというのは、それぞれの化学ポテンシャルが同じになっていると考えます。
両辺が二変数関数となっているので、例えば\(x+y=3x^2+x-2y+1\)のような方程式を考えるようなことをイメージしてください。
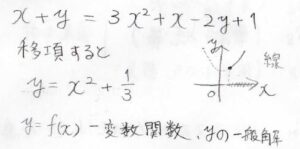
これを移項すると、\(y=x^2+1/3\)となり、\(x\)の関数として、\(y\)の一般解が得られます。
このとき、\(xy\)平面上では、\(y=x^2+1/3\)という曲線上の点すべてが解となるわけです。
そして、それに\(\gamma\)相を加えた3つの相が共存しているときには、3つの化学ポテンシャルが等しくなります。
\(x\)と\(y\)の二変数関数に例えるならば、\(x+y=3x^2+x-2y+1=-x+3y-5\)みたいなイメージです。
これを解くと、\(x\)と\(y\)の解は文字を含まない値として求められます。
これを\(xy\)平面上で図示すると点になるので、\(3\)相系は可変度が\(0\)だというわけです。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
