こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(harmonic oscillator)
それでは、内容に入っていきます。!
調和振動子とは
まず、調和振動子とは何かという話から入ります。
一言でいえば、ばねのことです。
高校物理をとっていた方ならわかると思いますが、ばねの単振動が調和振動子の例になります。
ポテンシャルが\(\displaystyle \frac{1}{2}kx^2\)で与えられます。
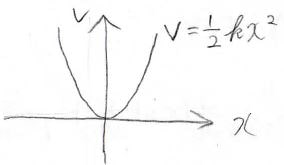
ここで、\(\displaystyle k\)は力の定数(ばね定数)、\(\displaystyle x\)は自然長からの変位です。
古典力学での調和振動子では、時刻\(t\)での物体の位置を三角関数で表すことができますが、これが量子になった場合は、どのような解が得られるのでしょうか?
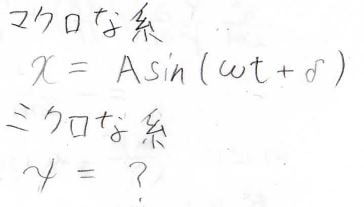
シュレディンガー方程式の変形
ポテンシャルは古典力学のときと同様なので、シュレディンガー方程式は下の形になります。
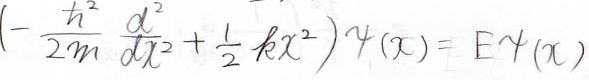
ここから変形をしていきます。
まず、\(\xi=\alpha x\)とします。(\(\xi\)はグザイと読みます。)
\(\alpha\)は、この形で与えられるものとします。
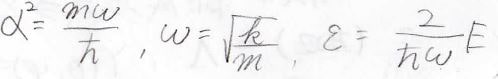
また、エネルギーに比例する量として、\(\varepsilon\)も上のようにおいておきます。
変数を\(x\)から\(\xi\)に変えると、このような形の式になります。
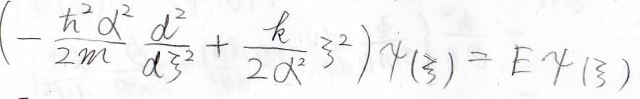
これの両辺に\(\displaystyle \frac{2}{\hbar \omega}\)をかけて整理すると、ここまで簡単な式にすることができます。
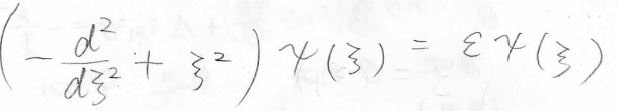
仮に\(\xi\)が無限大のには、下の形に近似できます。
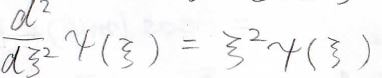
ここから波動関数の形を考えると、下の形になります。
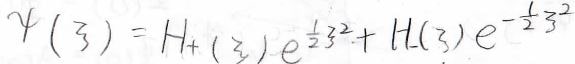
\(H\)というのが\(\xi\)の関数になっています。
\(\xi\)が無限大のときにはポテンシャル無限大なので、\(\psi=0\)となり、結局\(e\)のマイナス乗の項だけが残ります。
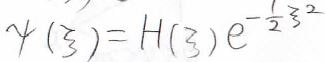
これを使って微分を計算すると、このようになります。
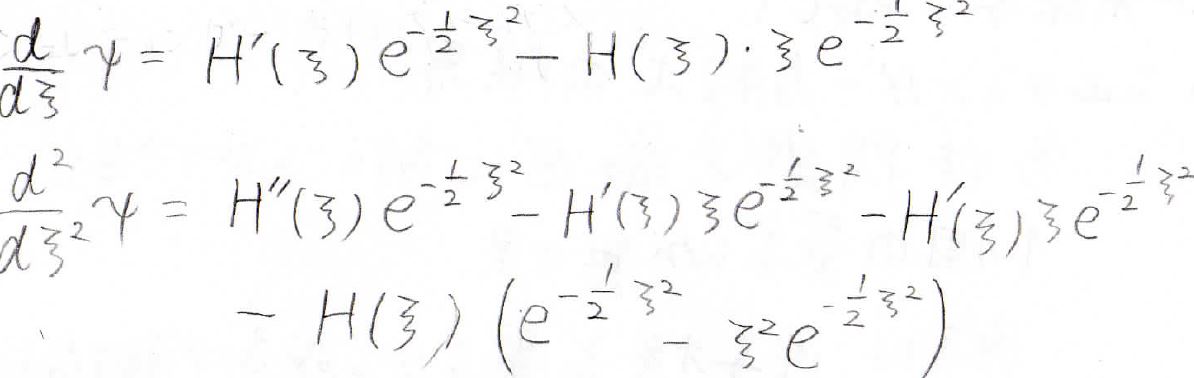
それをシュレディンガー方程式に代入したものが下の式です。
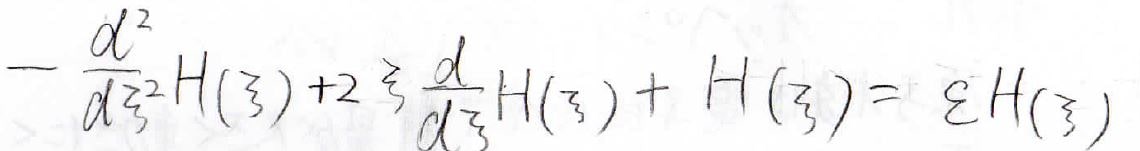
これを満たす\(H\)の関数群は数学的に解かれており、波動関数は下のような形で与えられます。
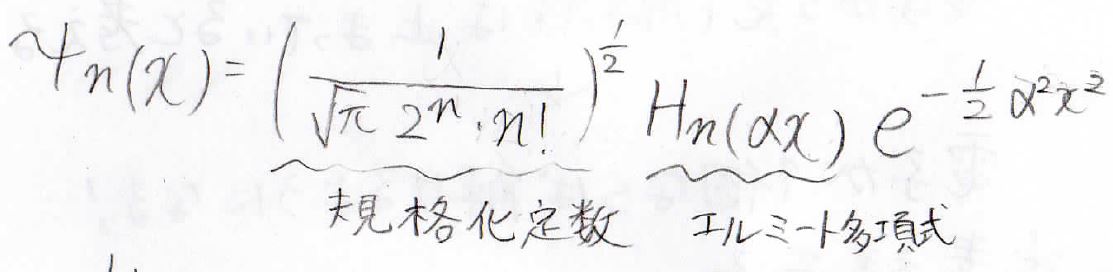
係数部分は規格化定数です。
そしてここの\(H_n\)はエルミート多項式と呼ばれています。
そして、先ほど導出したように\(\displaystyle \exp(-\frac{1}{2}\xi ^2)\)が最後にかかってきます。
エルミート多項式\(H_n\)は下のような式です。
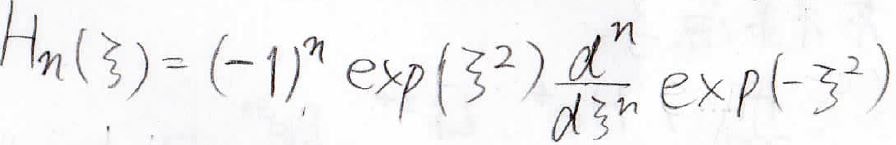
このようにして求められた波動関数は、直交性を満たしています。
直交性とは、量子数\(n\)が異なる波動関数同士の積を全空間で積分すると\(0\)になる性質のことです。
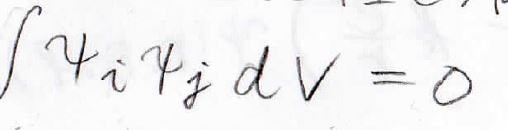
直交性を満たす状態間では相関がなく、それぞれが独立であるという意味になります。
振動エネルギー
波動関数がわかると、エネルギーも計算できます。
\(\psi\)はかなり複雑な形でしたが、エネルギーは簡単な形になって、\(\displaystyle (n+\frac{1}{2})\hbar \omega\)となります。
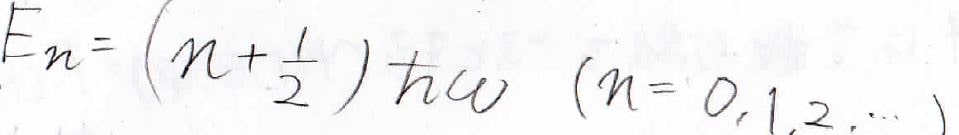
このエネルギー準位の特徴は、まず状態間のエネルギー差が\(\hbar \omega\)で一定になることです。
これは実験からも確かめることができます。
詳しくは、こちらを参照してください。

そして、\(n\)が\(0\)のとき、すなわち最も安定な状態のエネルギーが\(\displaystyle \frac{1}{2}\hbar \omega\)となって、\(0\)にならないということがとても重要になります。
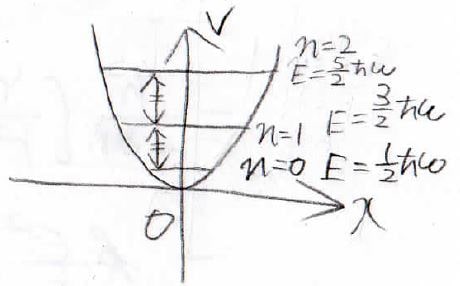
量子の不確定性から考えてもイメージできると思いますが、量子は1点にとどまることなく、ある存在確率で雲のように分布しています。
エネルギーが\(0\)のとき、\(x\)は\(0\)をとるしかないので、これは量子では起こらないということになります。
この、最安定状態での振動を零点振動、エネルギーのことを零点振動エネルギー、または零点エネルギーと呼びます。
仮に共有結合をばねに見立てた場合には、温度が\(0\ \rm{K}\)近傍でも、この結合は振動し続けるということになるので、結合の長さは一定ではなく時間変化しているということがわかります。

熱力学で扱う内部エネルギーなどの状態量は、\(0\ \rm{K}\)での有限の値が基準にされることが多いので、知っておいてください。
練習問題
それでは、練習問題をやってみます。
\(n\)が\(0\)と\(1\)のときのエルミート多項式を求めて、実際にエネルギーを求めてくださいという問題です。
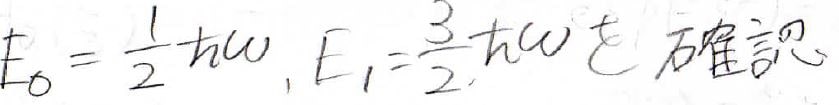
まず、\(n=0\)のとき、\(H=1\)になるので、\(\psi\)はこのようになります。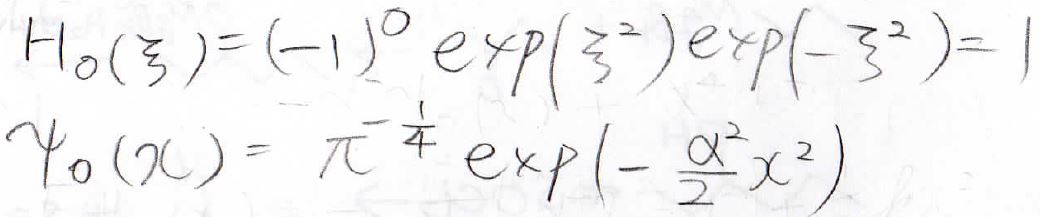
これの二階導関数は\(\psi_0\)を使って、下のように書けるので、これをシュレディンガー方程式に入れます。
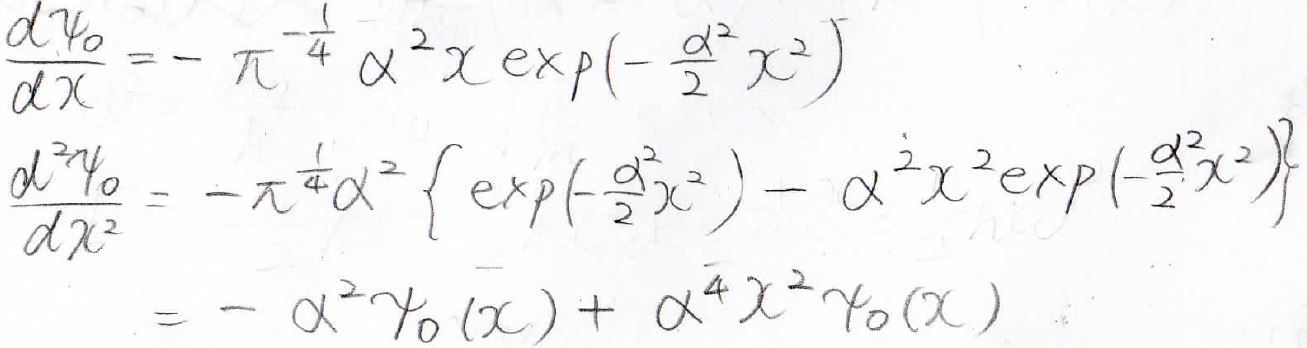
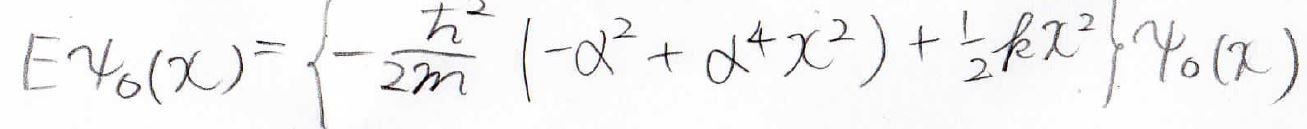
それから\(\alpha\)を元に戻すと、ポテンシャルエネルギーがキャンセルして、\(\displaystyle \frac{1}{2}\hbar \omega\)だけが残ってきます。
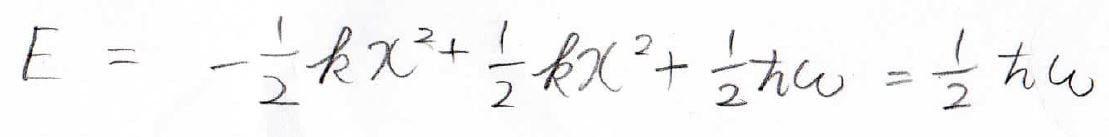
\(n=1\)の場合も同様にできて、エネルギーが\(\displaystyle \frac{3}{2}\hbar \omega\)と出てきます。
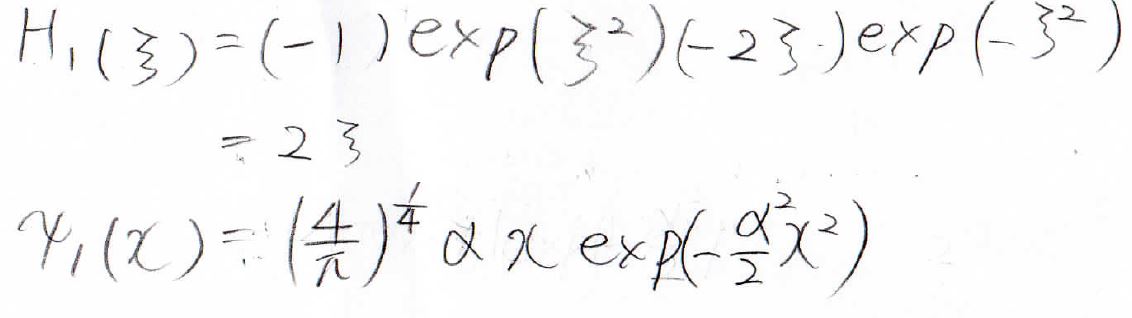
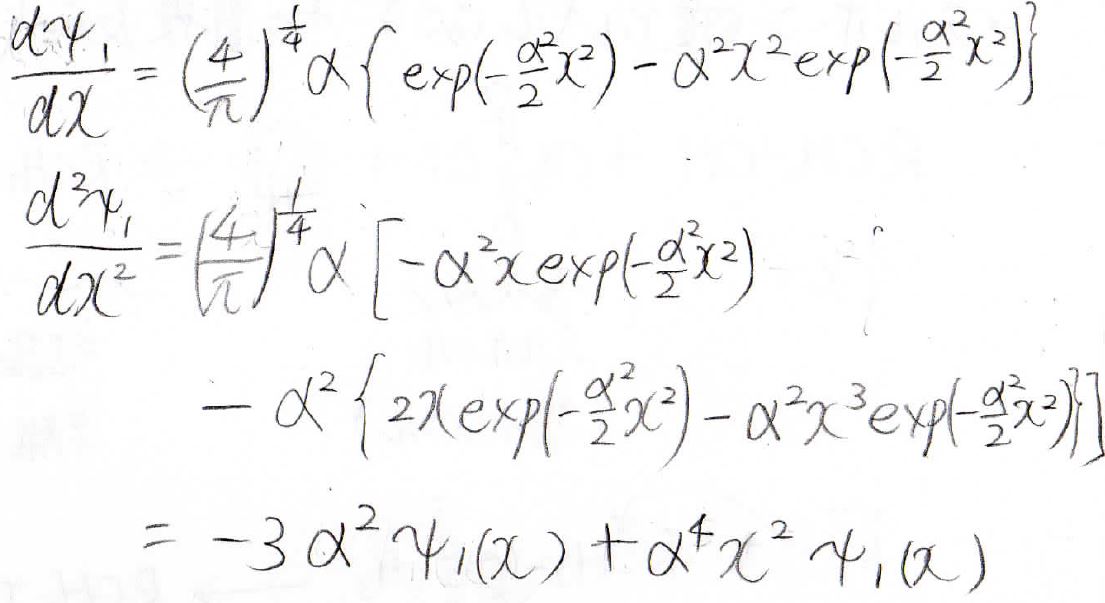
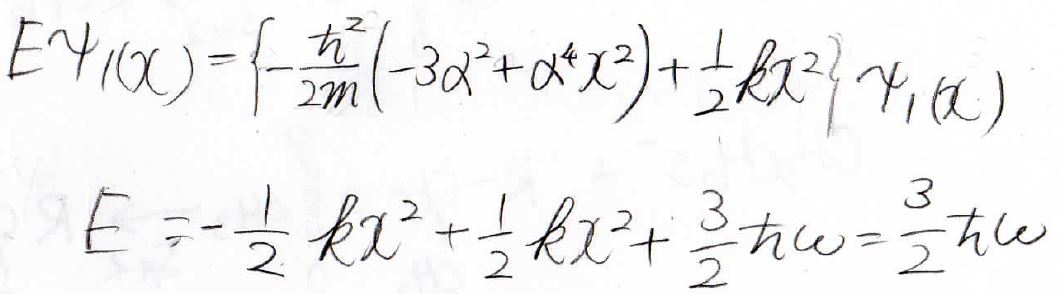
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




