こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Le Chatelier’s principle)
平衡定数と圧力の関係
始めに、平衡定数が圧力によってどのように変化するのかを考えてみましょう。
平衡定数\(K\)は、全体で反応ギブズエネルギーが\(0\)となる組成における反応商であり、\(\displaystyle \exp{(-\frac{\Delta_\rm{r} \mathit{G^\circ}}{RT})}\)で表されます。
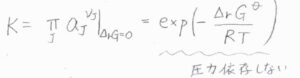
\(\Delta_\rm{r}\)\( G^\circ\)は標準反応ギブズエネルギー、\(R\)は気体定数、\(T\)は絶対温度です。
この式を見ると、\(\Delta_\rm{r}\)\( G^\circ\)は定数であり、平衡定数は圧力に依存しないことがわかります。
したがって、フガシティ―係数を\(1\)と仮定すると、\(T\)一定のとき、\(\displaystyle \prod_\rm{J}\)\(\displaystyle (\frac{p_\rm{J}}{p^\circ})^{\nu_\rm{J}}\)が一定になります。
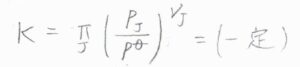
分子数が変化しないとき
まず、反応によって分子数が変化しない\(\rm{A}\)\(+\rm{B}\)\(\rightleftharpoons \rm{C}\)\(+\rm{D}\)という反応について考えてみます。
すべての化学種が理想気体であるとすると、任意の化学種\(\rm{J}\)について、その分圧\(p_\rm{J}\)はモル分率を\(x_\rm{J}\)と全圧\(p\)の積で書けます。
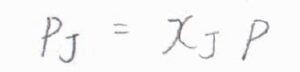
ここで、全圧を\(p\)から\(p+\Delta p\)まで加圧したときの平衡定数の変化を考えます。
加圧前の平衡定数は\(\displaystyle \frac{x_\rm{C}\mathit{x}_\rm{D}(\mathit{p/p}^\circ)^2}{x_\rm{A}\mathit{x}_\rm{B}(\mathit{p/p}^\circ)^2}\)、加圧後の平衡定数は\(\displaystyle \frac{x_\rm{C}’\mathit{x}_\rm{D}'[(\mathit{p}+\Delta \mathit{p})/\mathit{p}^\circ]^2}{x_\rm{A}’\mathit{x}_\rm{B}'[(\mathit{p}+\Delta \mathit{p})/\mathit{p}^\circ]^2}\)であり、これらが等しくなります。
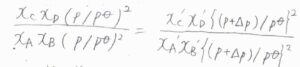
約分すると圧力が消えて、\(\displaystyle \frac{x_\rm{C}\mathit{x}_\rm{D}}{x_\rm{A}\mathit{x}_\rm{B}}=\frac{x_\rm{C}’\mathit{x}_\rm{D}’}{x_\rm{A}’\mathit{x}_\rm{B}’}\)となるため、モル分率は全圧によって変化しないということになります。
分子数が変化するとき
次に\(\rm{A}\)\(\rightleftharpoons 2\rm{B}\)というように、1分子が2分子に解離する反応について考えていきます。
そのときには、約分しても圧力が残ってしまいます。
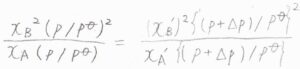
整理すると、\(\displaystyle \frac{x_\rm{B}^2}{x_\rm{A}}=\frac{(p+\Delta p)}{p}\frac{(x_\rm{B}’)^2}{x_\rm{A}’}\)という関係になります。
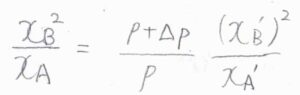
加圧したとき、\(p+\Delta p \gt p\)であるため、\(\displaystyle \frac{x_\rm{B}^2}{x_\rm{A}} \gt \frac{(x_\rm{B}’)^2}{x_\rm{A}’}\)となります。
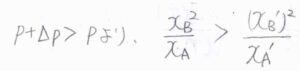
したがって、加圧すると\(\rm{A}\)が増加して\(\rm{B}\)が減少することになります。
一般的には、分子数が減少する方向へ平衡が移動します。
ルシャトリエの原理とは、化学平衡状態にある系に何らかの変化が生じた際に、その変化を相殺する方向に平衡が移動するというものです。
先ほどの分解反応においては、圧力の増大を打ち消すために、全体の分子数を減少させる方向へ平衡が平衡が移動したということです。
\(\rm{A}\)の反応率を\(\alpha\)として、\(\alpha\)の全圧依存性を考えると、次のようになります。
反応前は、\(\rm{A}\)が\(n\ \rm{mol}\)あったとします。
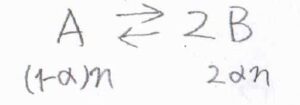
平衡状態に達したとき、\(\rm{A}\)は\(\alpha n\)だけ消費されたことになるので、\(\rm{A}\)の物質量は\((1-\alpha)n\)と書けます。
そして、\(\rm{B}\)は消費された\(\rm{A}\)の\(2\)倍生成されるので、\(\rm{B}\)の物質量は\(2\alpha n\)となります。
したがって、\(\rm{A}\)のモル分率\(x_\rm{A}\)は\(\displaystyle \frac{1-\alpha}{1+\alpha}\)、\(\rm{B}\)のモル分率\(x_\rm{B}\)は\(\displaystyle \frac{2\alpha}{1+\alpha}\)と書かれます。
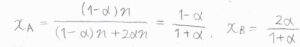
平衡定数\(\displaystyle K=\frac{x_\rm{B}^2\mathit{p}}{x_\rm{A}\mathit{p}^\circ}\)であり、これが\(\displaystyle \frac{4\alpha^2p}{(1+\alpha)(1-\alpha)p^\circ}\)と書かれます。
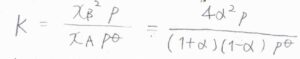
この関係を整理すると、\(\displaystyle \alpha=\sqrt{\frac{1}{1+4p/Kp^\circ}}\)となります。
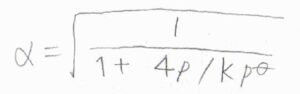
全圧がとても小さいときには、\(\alpha\)がほぼ\(1\)となるので、ほとんどの\(\rm{A}\)が分解することになります。

全圧を大きくするほど、\(\alpha\)は小さくなり、\(\rm{A}\)が残ることになります。
平衡定数と温度の関係
続いて、平衡定数の温度変化について考えていきましょう。
冒頭で示した平衡定数と標準反応ギブズエネルギーの関係式について、両辺の対数をとると、\(\displaystyle \ln{K}=-\frac{\Delta_\rm{r}\mathit{G}^\circ}{RT}\)となります。

さらに両辺を温度\(T\)について微分すると、右辺はギブズ-ヘルムホルツの式より、\(\displaystyle \frac{\Delta_\rm{r}\mathit{H}^\circ}{RT^2}\)となります。
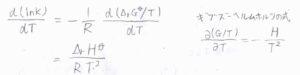
この式をファント-ホッフの式と言います。
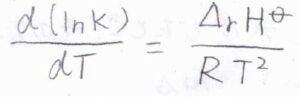
\(T\)の逆数を\(T\)について微分すると\(\displaystyle -\frac{1}{T^2}\)になることを利用して、\(\displaystyle \frac{\rm{d}(\ln{\mathit{K}})}{\rm{d}(1/\mathit{T})}=-\frac{\Delta_\rm{r}\mathit{H}^\circ}{R}\)という形に変形させることもできます。
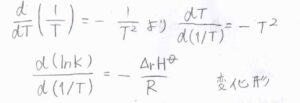
温度を上昇させたときに平衡定数が大きくなるか小さくなるかは、標準反応エンタルピーの符号によって決まります。
反応エンタルピーが正(吸熱反応)のときには、昇温に伴い平衡定数は大きくなります。
したがって、平衡は生成系側へ動きます。
反対に、反応エンタルピーが負(発熱反応)のときには、昇温に伴い平衡定数は小さくなります。
平衡は反応系側へ動くことになります。
横軸を\(T\)の逆数、縦軸を\(\ln{K}\)としてグラフにしたものは、ファント-ホッフプロットと呼ばれ、標準反応エンタルピーの温度変化が無視できるときには、このような一次関数になります。

傾きが\(\displaystyle -\frac{\Delta_\rm{r}\mathit{H}^\circ}{R}\)で、縦軸の切片が\(\displaystyle \frac{\Delta_\rm{r}\mathit{S}^\circ}{R}\)です。
反応エンタルピーの符号によって、右上がりか右下がりかが決まります。
このプロットを使えば、熱量の測定をせずに標準反応エンタルピーと標準反応エントロピーを決定することができます。
分子論的解釈
最後に、平衡定数の温度変化について、ボルツマン分布から分子論的に考察してみます。
まず、順反応が吸熱反応である場合を、生成系のエネルギー準位が反応系のものよりも全体的に高エネルギー側にある系に見立ててみます。

分子数変化はないものとしています。
温度を上げることで、低エネルギー側にあった分子が減少し、高エネルギー側にも分子が分布するようになります。
これにより、分子が生成系にある確率が高くなるので、平衡は生成系側へ移動することになります。
反対に発熱反応では、生成系側がより低いエネルギー状態をとる系で考えると、昇温により生成系側に分子が存在する確率が下がります。
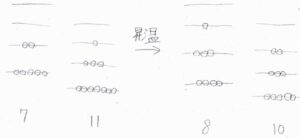
つまり、反応系側へ平衡が移動することになります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!