こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(heat capacity)
それでは内容に入っていきます!
熱容量の定義、比熱との区別
まず、熱容量の定義からおさらいしていきましょう。
言葉で言うと、熱容量とは単位温度分だけ上昇させるのに必要な熱量であり、式で表すと、系に与えられた微小な熱量を微小な温度変化で割った値になります。
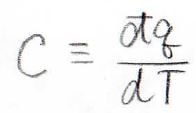
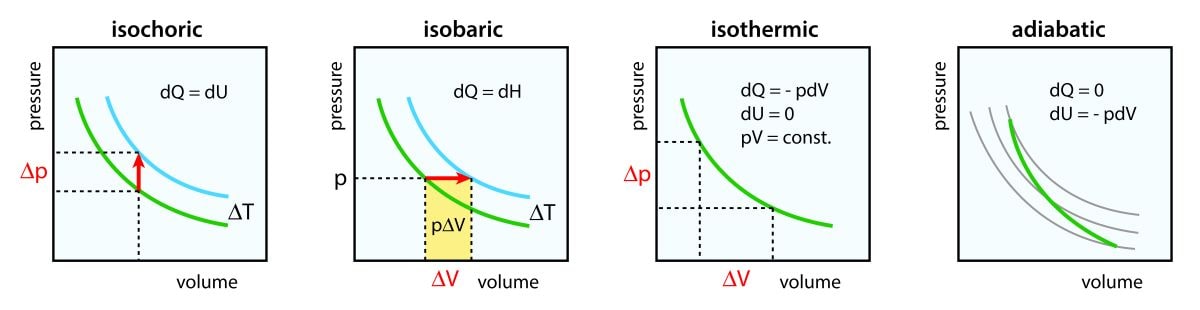
定積変化、定圧変化については、こちらをご覧ください。
そして、当然と言えば当然ですが、\(1 \rm{mol}\)の気体と\(2 \rm{mol}\)の気体であれば、\(1 \rm{mol}\)の方が少ない熱量で温度を上げることができるため、この熱容量という値は物質量に比例していることになります。
このように物質量に比例し、物質定数とならない状態量は示量性であるといいます。

示量性である状態量はほかに内部エネルギー\(U\)や体積\(V\)が当たります。
文献等で結果を比較する場合には、実験条件に依存しない値が必要なので、このような示量性の状態量は\(1 mol\)あたりの量で考えることが多いです。
\(1 \rm{mol}\)あたりの熱容量はモル熱容量、もしくはモル比熱や分子熱などと呼ばれ、物質量に依存しないので、このような状態量は示量性に対して示強性であるといいます。
示強性の状態量はほかに、圧力\(p\)や温度\(T\)、モル体積\(V_m\)などが当たります。
また、質量当たりの熱容量を表す比熱も示強性です。
なぜ圧力や温度が示強性で、体積が示量性なのかは、次のように説明できます。
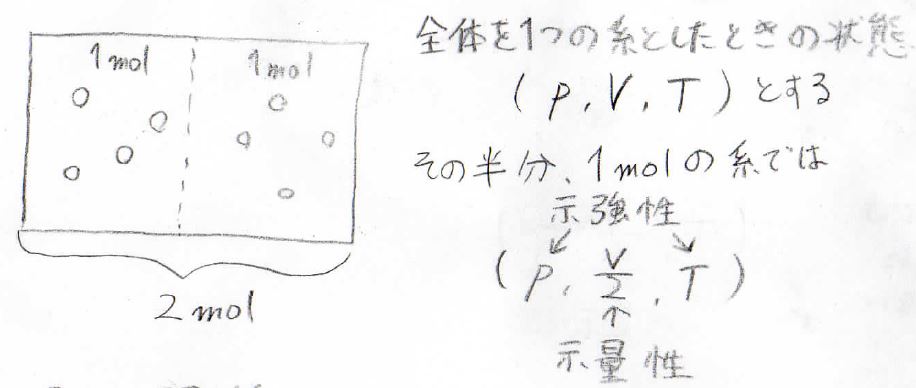
まず\(2 \rm{mol}\)の気体分子があるとします。
その圧力、体積、温度はそれぞれ\(p\)、\(V\)、\(T\)です。
ここで\(2 \rm{mol}\)あるうちの半分、\(1 \rm{mol}\)の分子についてのみ考えてみましょう。
これらの分子についてでは、圧力、体積、温度はそれぞれ\(p\)、\(V/2\)、\(T\)となります。
半分に分けたところで、温度が下がるようなことは起こらず、またそこだけ低い圧力であるということはないということです。
定積熱容量と定圧熱容量の関係
それでは、熱容量は物質量に比例する示量性の状態量であることを踏まえて次の話に入っていきます。
ここからは定積熱容量と定圧熱容量がどういう関係になっているのかを考えていきます。
これは前回もお話ししましたが、定積熱容量は体積一定下で内部エネルギー\(U\)を温度\(T\)で偏微分した値、定圧熱容量は圧力一定下でエンタルピー\(H\)を温度\(T\)で偏微分した値です。
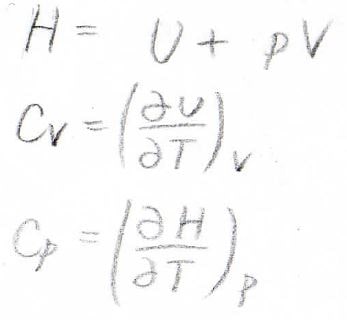
ここでエンタルピーは、内部エネルギー\(U\)に圧力\(p\)と体積\(V\)の積を足した値として定義された状態量です。
それではここから熱容量の関係を考えていきます。
まずは内部エネルギー\(U\)が温度と体積を変数に持つ二変数関数であるということを考えましょう。
理想気体であれば、\(U\)は温度にのみ依存するはずなので、これはもっと一般的な考え方になります。
そして、この\(U\)に関して、その全微分はこのように書けます。
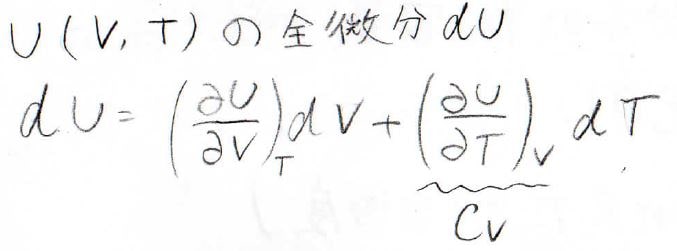
全微分については、こちらを参照してください。

ここで第二項には、定積熱容量\(C_V\)が出てきます。
続いて、定圧変化を考えるために、圧力一定条件として、\(U\)を\(T\)で偏微分します。
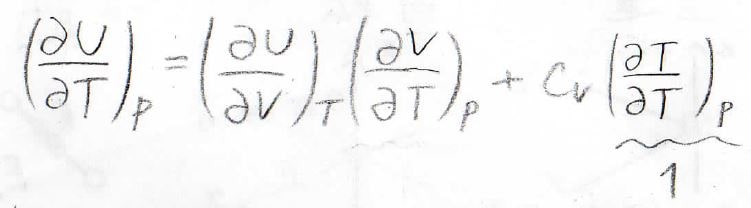
第二項については、\(T\)を\(T\)で偏微分している部分が\(1\)となり、\(C_V\)という定数になります。
次に定圧熱容量\(C_\rm{p}\)について考えてみると、\((\frac{\partial p}{\partial T})_p=0\)となるため、2つの項となります。
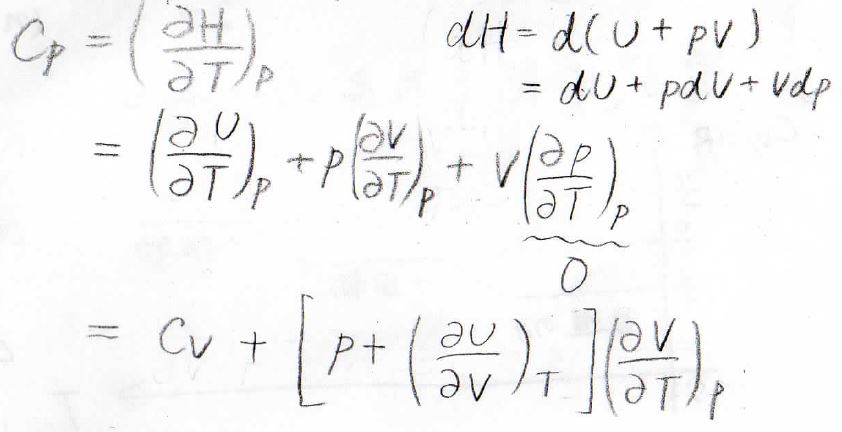
そして、先ほど求めた\((\frac{\partial U}{\partial T})_p\)を代入し、\((\frac{\partial V}{\partial T})_p\)で括ると、↑のようになります。
理想気体の時には、\((\frac{\partial U}{\partial V})_T=0\)であり、理想気体の状態方程式より、\((\frac{\partial V}{\partial T})_p=\frac{nR}{p}\)となります。
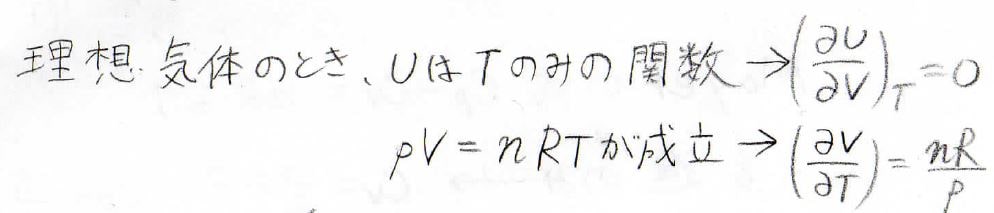
したがって、\(C_p-C_V=p \frac{nR}{p}\)、すなわち\(nR\)となります。
理想気体の定積熱容量と定圧熱容量の関係を表すこの式は、Mayerの式と言います。
理想気体ではない場合については、また別の機会にやっていきます。
熱容量の温度依存性
それでは最後に、二原子理想気体分子について、その熱容量を考えていきましょう。
ここでは等分配則により、内部エネルギーが\(\frac{1}{2}RT \times\)自由度で表されます。
分子が持つエネルギー状態には4種類があり、それは並進、回転、振動、電子状態です。
ここでは、電子を除く3つについて考えていきましょう。
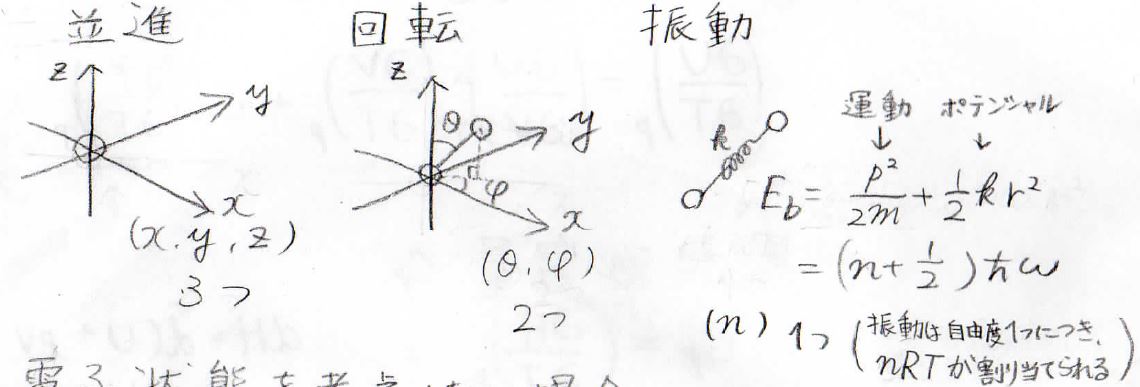
三次元空間で考えると、まず並進運動は二原子あるうちの一方の原子の座標で\(x\)、\(y\)、\(z\)を独立に取ることができるため、自由度は3つになります。
回転では、さっき座標を決めた原子から見てもう一方の原子がどの方向にあるのかを考えます。
したがって三次元極座標における角度の変数\(\theta\)と\(\phi\)の2つが自由度になります。
振動は、2つの原子間距離に影響します。
結合をばねとして考えると、そのばねの振動状態を表す量子数がその自由度となり、二原子分子の場合は1つになります。
そして、ここが重要なことなのですが、これらの自由度は低温では自由度として数えられません。
ボルツマン分布を考えると分かりやすいのですが、基底状態と第一励起状態の間のエネルギー差に対して温度が小さすぎるときには、その分子数の比が\(0\)に近い値となり、基底状態に集中します。
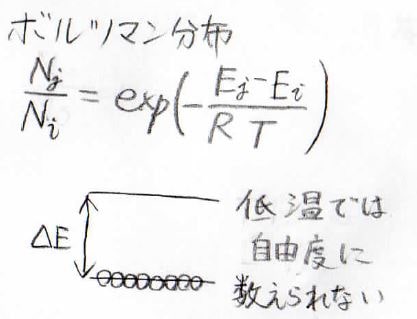
こうなると、独立な変数とは呼べなくなります。
したがって熱容量は温度によって変化することになります。
そのエネルギー間隔の大小関係により、温度上昇に伴って並進、回転、振動の順番で寄与するようになります。
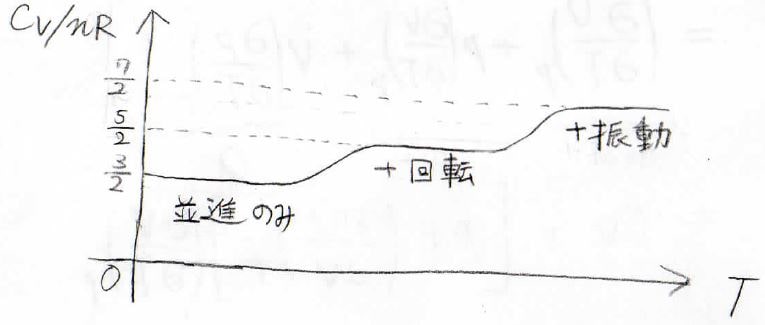
ここで、最も高温における定積熱容量が\(\frac{7}{2}nR\)となっていますが、振動の自由度に関しては1つにつき\(nR\)の寄与があります。
これはばね1つについて運動エネルギーとポテンシャルエネルギーのそれぞれに\(\frac{1}{2}nR\)の寄与があるからです。
そして、Mayerの式より、定積熱容量に\(nR\)を足した値が定圧熱容量となるので、単原子分子も含めて並進しかきかないときには、\(C_p=\frac{5}{2}nR\)、回転もきくときには、\(C_p=\frac{7}{2}nR\)、振動も含むときには\(C_p=\frac{9}{2}nR\)となります。

まとめ
はい、それでは今回の内容は以上なので、最後おさらいをやって終わります。
今回は定積熱容量と定積熱容量の関係について考えました。
内部エネルギーを体積と温度の関数と考え、その偏微分からその関係を導くと、理想気体の時にはMayerの式が成り立つことが分かります。
ここで、熱容量は物質量に比例する量なので、\(C_p-C_V\)も\(nR\)というように\(n\)に比例しています。
そして、二原子理想気体分子では温度の上昇とともに並進、回転、振動の順番で自由度として熱容量に寄与するようになり、\(C_V\)は\(\frac{3}{2}nR\)、\(\frac{5}{2}nR\)、\(\frac{7}{2}nR\)と変化していきます。
Mayerの式より、\(C_p\)は\(\frac{5}{2}nR\)、\(\frac{7}{2}nR\)、\(\frac{9}{2}nR\)となります。
ここで、振動については自由度1つにつき運動エネルギーとポテンシャルエネルギーを考えるため、熱容量に\(nR\)だけ寄与するということに注意しましょう。
以上です。
どうもありがとうございました!