こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Lindemann–Hinshelwood mechanism)
それでは内容に入っていきます!
前駆平衡
始めに考える前駆平衡とは、このような反応です。
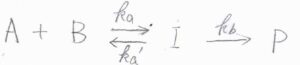
反応物\(\rm{A}\)と\(\rm{B}\)から中間体\(\rm{I}\)を経由して、生成物\(\rm{P}\)ができます。
\(\rm{A}\)\(+\rm{B}\)と\(\rm{I}\)は化学平衡となっており、順反応である\(2\)次素反応と逆反応の\(1\)次素反応の反応速度定数をそれぞれ\(k_\rm{a}\)、\(k_\rm{a’}\)とします。
\(\rm{I}\)から\(\rm{P}\)への\(1\)次素反応の反応速度定数は、\(k_\rm{b}\)とします。
\(\rm{A}\)\(+\rm{B}\)と\(\rm{I}\)が平衡状態であるためには、\(\rm{I}\)から\(\rm{P}\)への反応よりも\(\rm{I}\)から\(\rm{A}\)\(+\rm{B}\)への逆反応の方が速く進行する必要があるため、ここでは\(k_\rm{a’}\)\(\gg k_\rm{b}\)と仮定します。
活量係数がすべて\(1\)のとき、平衡定数\(K\)は、\(\displaystyle \frac{[\rm{I}]\mathit{c}^\circ}{[\rm{A}][\rm{B}]}\)と書けます。
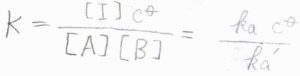
ここで、\(c^\circ\)は標準モル濃度です。
反応速度定数を使って書くと、\(\displaystyle K=\frac{k_\rm{a}\mathit{c}^\circ}{k_\rm{a’}}\)となります。
\(\rm{P}\)の生成速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}=k_\rm{b}\)\([\rm{I}]\)より、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}=\frac{k_\rm{b}\mathit{K}}{c^\circ}[\rm{A}][B]\)となります。
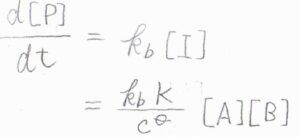
したがって、この反応の反応次数は\(2\)となります。
そして、全体の反応を、中間体を経由しない\(\rm{A}\)\(+\rm{B}\)\(\longrightarrow \rm{P}\)という1段階の反応であるとみなしたときの見かけ上の反応速度定数\(k_\rm{all}\)は、\(\displaystyle \frac{k_\rm{b}\mathit{K}}{c^\circ}\)となり、これは\(\displaystyle \frac{k_\rm{a}\mathit{k}_\rm{b}}{k_\rm{a’}}\)とも書けます。
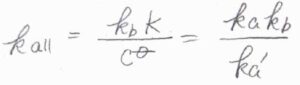
アレニウスの式に当てはめると、\(E_\rm{a,a}\)\(+E_\rm{a,b}\)\(-E_\rm{a,a’}\)が見かけ上の活性化エネルギーになります。
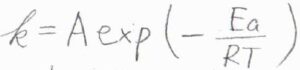
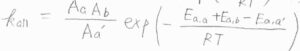
これを反応の有効活性化エネルギーと言います。
つまり、反応次数は1段階目の順反応と同じで\(2\)となりますが、反応速度定数には、3つそれぞれの活性化エネルギーがすべて関与します。
逆反応の活性化エネルギーが小さいほど、\(\rm{P}\)の生成速度は遅くなります。
リンデマン-ヒンシェルウッド機構
続いて、リンデマン-ヒンシェルウッド機構というモデルについて考えます。
まず1段階目では、反応物\(\rm{A}\)が2分子で衝突すると、一方が活性化して\(\rm{A}\)\(^\ast\)になります。

この\(\rm{A}\)\(^\ast\)は、再び\(\rm{A}\)と衝突したときに、エネルギーを失って安定な\(\rm{A}\)と戻ることがあります。
そして2段階目、\(\rm{A}\)\(^\ast\)の一部が生成物\(\rm{P}\)へと変化します。
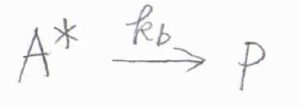
同じ化学種どうしで1段階目の反応が起こることと、1段階目の逆反応も\(2\)次素反応となることが、先ほどの前駆平衡と異なる点です。
中間体である\(\rm{A}\)\(^\ast\)について、定常状態近似を適用します。
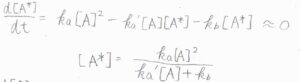
\(\displaystyle \frac{\rm{d}[A^\ast]}{\rm{d}\mathit{t}}=k_\rm{a}\)\([\rm{A}\)\(]^2-k_\rm{a’}\)\([\rm{A}\)\(][\rm{A}\)\(^\ast]-k_\rm{b}\)\([\rm{A}\)\(^\ast]\)であり、これを\(0\)とします。
これを整理すると、\([\rm{A}^\ast]\)\(\displaystyle =\frac{k_\rm{a}[\rm{A}]^2}{k_\rm{a’}[\rm{A}]+\mathit{k}_\rm{b}}\)となります。
\(\rm{P}\)の生成速度は、\(k_\rm{b}\)\([\rm{A}\)\(^\ast]\)であるため、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}=\frac{k_\rm{a}\mathit{k}_\rm{b}[\rm{A}]^2}{k_\rm{a’}[\rm{A}]+\mathit{k}_\rm{b}}\)と書けます。
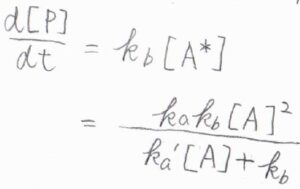
分母にも\([\rm{A}]\)があり、反応次数を単純に決めることができない形になります。
そこで、さらに条件を付けて反応次数を考えます。
\(\rm{A}\)の濃度がとても大きいときには、分母の\(k_\rm{a’}\)\([\rm{A}\)\(]+k_\rm{b}\)を\(k_\rm{a’}\)\([\rm{A}]\)と近似できます。
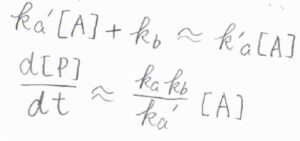
すると、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}t}=\frac{k_\rm{a}k_\rm{b}}{k_\rm{a’}}[\rm{A}]\)となります。
\(1\)次反応であることから、2段階目の\(\rm{A}\)\(^\ast\)から\(\rm{P}\)へと変化する段階が律速段階であることになります。
対して、\(\rm{A}\)の濃度がきわめて小さいときには、分母の\(k_\rm{a’}\)\([\rm{A}\)\(]+k_\rm{b}\)は\(k_\rm{b}\)とほぼ等しくなります。
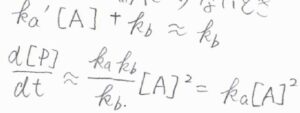
このとき、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}=k_\rm{a}[\rm{A}]^2\)となります。
濃度が低いと、そもそも衝突確率が低いため、1段階目の活性化の過程が律速段階となります。
逆反応である不活性化はほとんど起こらず、全体の反応速度にも影響しません。
以上のことより、反応次数は\(\rm{A}\)のモル濃度に依存するということになります。
\(1\)次以上にはなるので、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)を\([\rm{A}]\)でくくると、その係数を濃度依存する実効の反応速度定数\(k([\rm{A}\)\(])\)とみなすことができます。

これの逆数をとると、\(\displaystyle \frac{1}{k([\rm{A}])}=\frac{1}{k_\rm{a}}\frac{1}{[\rm{A}]}+\frac{k_\rm{a’}}{k_\rm{a}\mathit{k}_\rm{b}}\)となります。

横軸を\([\rm{A}]\)の逆数、縦軸を\(k([\rm{A}\)\(])\)の逆数としてグラフを書くと、このような一次関数になります。

その傾きと切片から、\(k_\rm{a}\)と\(\displaystyle \frac{k_\rm{a’}}{k_\rm{b}}\)が実験的に求められます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!