こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Michaelis–Menten mechanism)
それでは内容に入っていきます!
酵素とは
まず、酵素とは何かを簡単にお話しします。
酵素とは、生体内で起こる化学反応を触媒する分子のことです。
狭い意味での生体触媒とほとんど同じ意味の言葉です。
主な成分はタンパク質ですが、その表面にリン酸や短い糖鎖が修飾されているものも多くあります。
また、リボソームなど核酸との複合体となって、反応を触媒するものもあります。
そもそも触媒には、構成する元素や作用する場所などによってさまざまな分類方法があるわけですが、よくある分類方法としては均一触媒と不均一触媒があります。
均一触媒は、反応が起こる場所の相と触媒の相が同一である触媒のことを指します。
その相が液相である場合は、溶媒に溶けている状態で作用する触媒のことを均一触媒と言います。
例えば、生体内の水溶液中ではたらく酵素も均一触媒です。
タンパク質以外にも、塩や金属錯体などが該当することがあります。
反応が気相で起こる場合もあります。
対して、不均一触媒は、反応が起こる場所の相と触媒の相が同一ではない触媒のことを言います。
金属やその化合物を固体として、溶媒に溶解させずに用いるというのが工業的によく行われる手法です。
反応は、触媒の表面で起こります。
中学校の実験で、過酸化水素に二酸化マンガンを加えると、酸素が発生するというのがありましたが、それが不均一触媒反応の一例です。
酵素と言っても、例えば、細胞表面にあって、基質がある水溶液中には拡散せずに反応を起こすものは不均一触媒であると言えそうですが、あまりそのような区別は見かず、溶解させない無機物の触媒を指して言うことが多い印象です。
触媒のはたらきは、活性化エネルギーを下げることで反応速度を速くすることであり、ギブズエネルギーなどの熱力学量変化には影響しません。
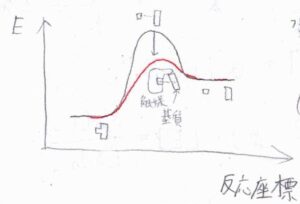
酵素を使うと、常温常圧の水溶液系というとても穏やかな条件で反応が起こるため、安全性やコストの面でも優れており、工業の分野でも実用化が進められています。
生成物の材料になる化合物を基質と言い、酵素と基質は鍵と鍵穴のように相性が合わないと触媒として機能しません。
これを基質特異性と言います。
基質と結合して、活性化する部分を活性部位と言いますが、活性部位以外のタンパク質の鎖も水素結合、ジスルフィド結合、疎水性相互作用などによって立体構造を保持するという役割を担っています。
ミカエリス-メンテン機構
さてここから、反応速度論の話に入っていきます。
酵素を\(\rm{E}\)、基質を\(\rm{S}\)、生成物を\(\rm{P}\)として、こちらの反応を考えます。
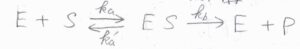
この機構は、ミカエリス-メンテン機構といわれるものです。
\(\rm{ES}\)というのは、酵素と基質の複合体を意味します。
反応開始時の酵素と基質の濃度は、それぞれ\([\rm{E}\)\(]_0\)、\([\rm{S}\)\(]_0\)であり、基質は酵素よりも十分に多く存在しているものとします。
反応が起こっている途中については、まず複合体を形成している酵素と形成していない酵素の濃度の和が\([\rm{E}\)\(]_0\)と書けます。
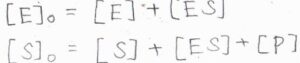
そして、反応前の基質、複合体中の基質、生成物の濃度の和が\([\rm{S}\)\(]_0\)となります。
ここで、酵素と基質の複合体\(\rm{ES}\)について、定常状態近似をします。
つまり、\(\displaystyle \frac{\rm{d}[\rm{ES}]}{\rm{d}\mathit{t}}=k_\rm{a}[E][S]\)\(-k_\rm{a’}[ES]\)\(-k_\rm{b}[\rm{ES}]=0\)です。
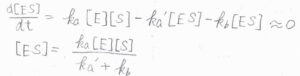
そうすると、\([\rm{ES}\)\(\displaystyle ]=\frac{k_\rm{a}}{k_\rm{a’}+\mathit{k}_b}[\rm{E}][\rm{S}]\)となります。
\(\displaystyle \frac{k_\rm{a’}+k_\rm{b}}{k_\rm{a}}\)はミカエリス定数と呼ばれるもので、ここでは\(K_\rm{M}\)と表すことにします。
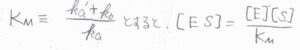
\(K_\rm{M}\)が小さいほど、酵素と基質の親和性が高く、解離やさらなる反応が起こりにくいことになります。
\([\rm{E}\)\(]=[\rm{E}\)\(]_0-[\rm{ES}]\)を\(\displaystyle [\rm{ES}]=\frac{[\rm{E}][S]}{\mathit{K}_\rm{M}}\)に代入して、再び\([\rm{ES}]\)について整理すると、\([\rm{ES}\)\(\displaystyle ]=\frac{[\rm{E}]_0}{1+K_\rm{M}/[S]}\)となります。
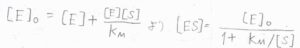
ここで、溶液中には基質がたくさんあるために反応中の濃度変化は無視できるものとします。
\(\rm{P}\)の生成速度\(v=k_\rm{b}\)\([\rm{ES}]\)であるため、\(\displaystyle v=\frac{k_\rm{b}[\rm{E}]_0}{1+K_\rm{M}/[\rm{S}]_0}\)となります。

横軸を\([\rm{S}]_0\)、縦軸を\(v\)としてグラフを書くと、こちらのようになります。
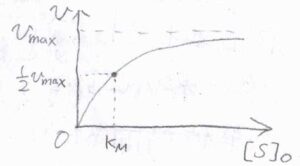
\([\rm{S}\)\(]_0\)が\(K_\rm{M}\)よりも十分小さいときには、分母の\(1+K_\rm{M}\)\(/[\rm{S}\)\(]_0\)を\(K_\rm{M}\)\(/[\rm{S}\)\(]_0\)と近似して、\(\displaystyle v=\frac{k_\rm{b}}{K_\rm{M}}[\rm{E}]_0[S]_0\)と書けます。
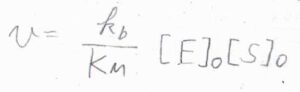
基質の濃度が低いときには、基質の濃度に比例して反応速度が大きくなります。
対して、\([\rm{S}\)\(]_0\)が\(K_\rm{M}\)に比べてとても大きなときには、分母の\(1+K_\rm{M}\)\(/[\rm{S}\)\(]_0\)が\(1\)と近似できるため、\(\displaystyle v=k_\rm{b}[E]_0\)となります。
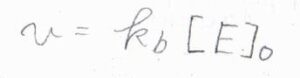
反応速度は基質の濃度には依存せず、ここで頭打ちになります。
基質の濃度が高いときには、酵素のほぼすべてが常に反応に関与する状態となっており、これ以上は速くなれないと解釈されます。
ミカエリス定数\(K_\rm{M}\)は、反応速度vがこの限界速度の\(\displaystyle \frac{1}{2}\)倍となるときの基質の濃度に相当します。
反応速度定数およびミカエリス定数を実験的に求めたいときには、まず反応速度の逆数をとって、\(\displaystyle \frac{1}{v}=\frac{1}{k_\rm{b}[\rm{E}]_0}+\frac{K_\rm{M}}{k_\rm{b}[E]_0}\frac{1}{[\rm{S}]_0}\)とします。
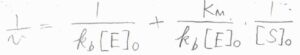
\(k_\rm{b}\)\([\rm{E}\)\(]_0\)は、先ほど求めた反応速度の最大値なので、\(v_\rm{max}\)と書き換えると、\(\displaystyle \frac{1}{v}=\frac{1}{v_\rm{max}}+\frac{K_\rm{M}}{v_\rm{max}}\frac{1}{[\rm{S}]_0}\)となります。
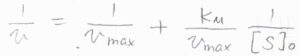
横軸に\([\rm{S}\)\(]_0\)の逆数、縦軸に\(v\)の逆数をとると、こちらのような一次関数のグラフが得られます。
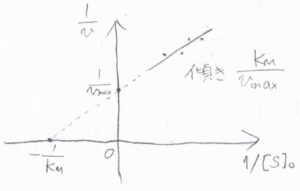
このプロットをラインウィーバー・バークのプロットと言います。
直線の傾きが\(\displaystyle \frac{K_\rm{M}}{v_\rm{max}}\)、縦軸の切片が\(\displaystyle \frac{1}{v_\rm{max}}\)となることから、\(v_\rm{max}\)と\(K_\rm{M}\)を求めることができます。
さらに、\(v_\rm{max}\)\(=k_\rm{b}\)\([\rm{E}\)\(]_0\)より、\(k_\rm{b}\)も計算できます。
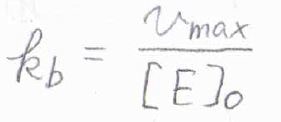
このプロットだけで、すべての反応速度定数を求めることはできませんが、ストップトフロー法など別の手法を組み合わせて、\(k_\rm{a}\)と\(k_\rm{a’}\)の一方さえわかれば、\(k_\rm{b}\)と\(K_\rm{M}\)がわかっているので、もう一方も計算することができます。
比較に用いる指標
ここで、複数の種類の触媒と1種類の基質、もしくは1種類の触媒と複数種類の基質で、触媒としてのはたらきを比較するときに用いる指標を紹介しておきます。
まずターンオーバー頻度という値です。
これは、単位時間あたりに生成物へと変換できる基質の最大量を指す言葉です。
\(k_\rm{cat}\)と表すことが多く、今回考えている系では、\(k_\rm{b}\)が\(k_\rm{cat}\)にあたります。
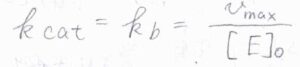
ただ、このターンオーバー頻度は複合体が形成してからの時間効率しか表しておらず、複合体を形成しない場合も考慮するときには、\(\displaystyle \frac{k_\rm{cat}}{K_\rm{M}}\)を使います。

これは、基質の濃度がとても高いときの見かけ上の反応速度定数で、特異定数と呼ばれることもあります。
\(K_\rm{M}\)が小さいほど酵素と基質の親和性が高く、また\(k_\rm{cat}\)が大きいほど複合体はより速く生成物を与えることになるので、\(\displaystyle \frac{k_\rm{cat}}{K_\rm{M}}\)は触媒の相対的な時間効率を表す値として使われます。
阻害機構
最後、酵素と基質のほかに阻害剤がある場合について、考えてみます。
阻害剤とは、酵素と結合はするものの、何か他の化学種へと変化することはなく、単純に酵素のはたらきを邪魔するような物質のことを言います。
ここでは、\(\rm{In}\)と表記することにします。
阻害は、酵素に結合するパターンと酵素と基質の複合体に結合するパターンの2つが起こりうるとします。
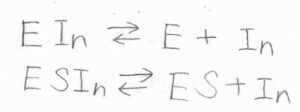
それぞれの平衡定数を\(K\)、\(K’\)とします。
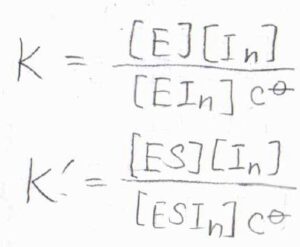
始めに、どちらの阻害も起こる場合から考えます。
この形は、非競合阻害もしくは混合型阻害と言います。
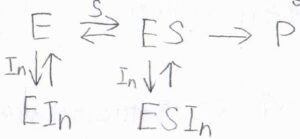
\(\rm{E}\)、\(\rm{EIn}\)、\(\rm{ES}\)、\(\rm{ESIn}\)のモル濃度の和は、時刻\(0\)における酵素のモル濃度\([\rm{E}\)\(]_0\)になります。
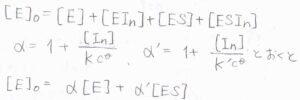
ここで\(\displaystyle 1+\frac{[\rm{In}]}{Kc^\circ}\)を\(\alpha\)、\(\displaystyle 1+\frac{[\rm{In}]}{K’c^\circ}\)を\(\alpha’\)とおくと、\([\rm{E}\)\(]_0=\alpha[\rm{E}\)\(]+\alpha'[\rm{ES}]\)と書けます。
\(\rm{ES}\)\(+\rm{In}\)と\(\rm{ESIn}\)が平衡状態となっているときには、定常状態近似の結果は阻害剤がないときと同じく、\([\rm{ES}\)\(\displaystyle ]=\frac{[\rm{E}][S]_0}{K_\rm{M}}\)となります。
\([\rm{E}]\)について解くと、\([\rm{E}\)\(\displaystyle ]=\frac{K_\rm{M}[\rm{ES}]}{[\rm{S}]_0}\)となり、これを上の式に代入すると、\([\rm{E}\)\(\displaystyle ]_0=(\frac{\alpha K_\rm{M}}{[\rm{S}]_0}+\alpha’)[\rm{ES}]\)となります。
したがって、\([\rm{ES}\)\(\displaystyle ]=\frac{[\rm{E}]_0}{\alpha K_\rm{M}/[\rm{S}]_0+\alpha’}\)と書けます。
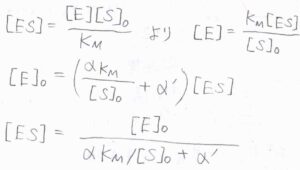
\(\alpha\)と\(\alpha’\)がともに\(1\)のときには、阻害剤がないミカエリス-メンテン機構の結果と一致します。
そして\(\rm{P}\)の生成速度\(v\)は、\(\displaystyle \frac{k_\rm{cat}[\rm{E}]_0}{\alpha K_\rm{M}/[\rm{S}]_0+\alpha’}\)となります。

両辺の逆数をとると、\(\displaystyle \frac{1}{v}=\frac{\alpha’}{v_\rm{max}}+\frac{\alpha K_\rm{M}}{v_\rm{max}}\frac{1}{[\rm{S}]_0}\)となります。
ここまできたら、さきほどの阻害機構で一方のパターンだけが起こっているときの反応速度も簡単にわかります。
阻害が起こっていないとき、平衡定数は無限大になります。
したがって、片方の阻害だけ考えるには、\(\alpha=1\)の場合と\(\alpha’=1\)の場合をそれぞれ考えればよいことになります。
\(\alpha\gt 1\)かつ\(\alpha’=1\)のとき、阻害剤は酵素だけに結合することができます。
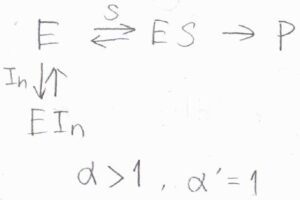
基質と阻害剤が酵素を奪い合うことから、これを競合阻害と言います。
\(\alpha =1\)かつ\(\alpha’ \gt 1\)のときには、阻害剤は複合体にのみ結合します。
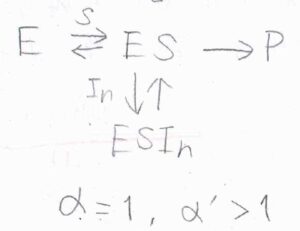
複合体を形成していない酵素は基質としか結合しないので、これを不競合阻害と言います。
以上のことを踏まえて、グラフを書くとこのようになります。
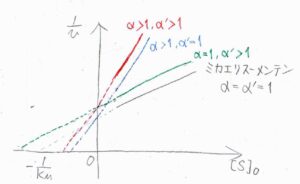
まず、黒が\(\alpha=1\)、\(\alpha’=1\)のミカエリス-メンテン機構です。
青が競合阻害で、縦軸の切片はそのまま傾きだけが大きくなります。
緑が不競合阻害で、傾きは変わらず切片だけが大きくなります。
非競合阻害では、傾きも切片も大きくなります。
阻害剤を入れる前後でグラフの傾きと切片のどちらが大きくなるのか、もしくはどちらも大きくなるのかを観察することでどの段階で阻害が起こっているのかを知ることができます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!