こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(multimolecularity)
それでは内容に入っていきます!
高分子の多分子性とは?
まず、低分子を考えてみましょう。
ここでは、エタンとn-ブタンを比べてみます。
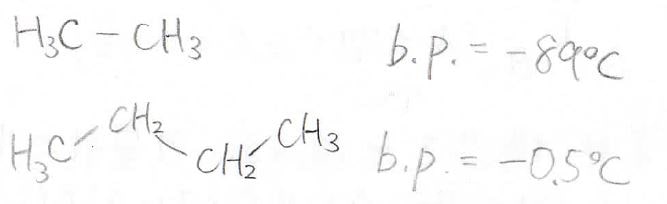
両者の違いは、炭素数2つですが、この違いは物性に大きく影響します。
例えば、沸点は\(\displaystyle 90^\circ \rm{C}\)近い差があります。
そのほかにも、融点や溶解度にも大きな違いが生じます。
では、高分子の場合はどうでしょうか。
例として、ポリエチレンの\(\displaystyle 10000\)量体と\(\displaystyle 10001\)量体を比べてみましょう。
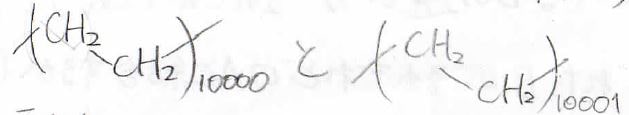
両者の違いは、先ほどのエタンとn-ブタンと同じく炭素数2つです。
しかし、割合で言えば、長さが\(\displaystyle 0.01\%\)伸びただけです。
この大きさの違いは、物性にはまったくと言ってよいほど影響しません。
融点、溶解度、密度、分解温度はほぼ同じになります。
ちなみに、高分子は大きすぎて、気体として存在できません。
温度を上げても、沸騰ではなく分解が起こって焦げるだけなので、沸点は存在しません。
このように高分子では分子量がまったく同じではなくても、似たような大きさであれば、ほぼ同じ物性を示すことは系を複雑にします。
一般的に、純物質を研究対象とする化学では、物性の違いを利用して単離します。
しかし、似たような大きさの高分子は物性の違いがほとんどないため、単離ができません。
そのため、合成高分子を扱う分野では、分子量や形状の異なる高分子の混合物を研究対象とします。
高分子試料の不均一性のことは、多分子性と言われます。
分子量分布と平均分子量
ここからは、多分子性をどのように考えるのかについて、話をしていきます。
まず、分子量に分布がある場合には、その分布がどのように広がっているのかということと、平均の分子量で議論します。
平均分子量の考え方は、いくつかあります。
モル分率の考え方
その中で最も簡単なのが、モル分率での考え方です。
\(\displaystyle n\)量体の物質量を\(\displaystyle N_n\)、\(\displaystyle n\)量体のモル分率を\(\displaystyle x_n\)とします。
すると、\(\displaystyle N_n\)と\(\displaystyle x_n\)は、このような関係になります。
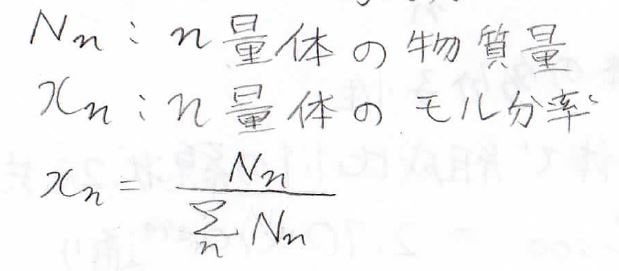
分母は、大きさの異なる分子の個数をすべて数え上げた、全分子の物質量です。
ここでさらに、数平均重合度\(\displaystyle P_\rm{n}\)という量を定義できます。
これは、期待値と同じように分子1個あたりの平均重合度を表したものです。
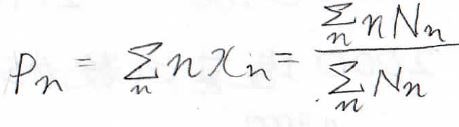
この数平均重合度にモノマー単位の分子量\(\displaystyle m_0\)をかけると、分子1個あたりの平均分子量になり、これは数平均分子量\(\displaystyle M_\rm{n}\)と呼ばれます。
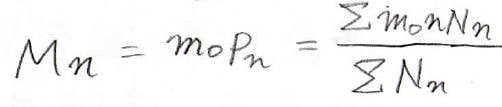
重量分率の考え方
そして、平均重合度の考え方には、重量分率を基準にしたものもあります。
\(\displaystyle n\)量体の重量分率を\(\displaystyle w_n\)で表すことにすると、\(\displaystyle w_n\)はこのように表されます。

\(\displaystyle n\)量体1モルの重量はモノマー単位\(\displaystyle m_0\)の\(\displaystyle n\)倍になるため、\(\displaystyle n\)量体の全重量はそれに物質量\(\displaystyle N_n\)をかけて、\(\displaystyle nm_0N_n\)になります。
分母は、総重量です。
重量平均の重合度\(\displaystyle P_\rm{w}\)もこのように定義できます。
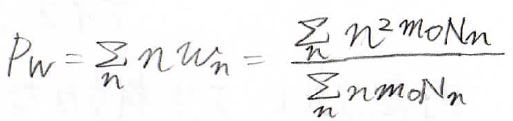
重量分率で重みを付けた平均量であるため、数平均よりも高分子量体に大きく影響される値になります。
同様に重量平均分子量\(\displaystyle M_\rm{w}\)も定義できます。

重縮合における\(\displaystyle M_\rm{n}\)、\(\displaystyle M_\rm{w}\)と分子量分布の評価方法
次に、\(\displaystyle M_\rm{n}\)と\(\displaystyle M_\rm{w}\)はどのような使い方をされるのかということをお話しします。
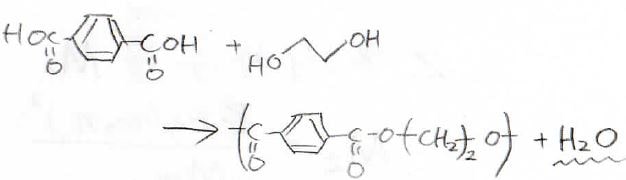
ここでは、重縮合反応でできた合成高分子を例にします。
重縮合とは一般的に、下に示すポリスチレンテレフタラート(PET)の合成反応のように、低分子の脱離を伴って起こる非連鎖重合を指します。
導出の過程はまた別の記事でお話ししますが、モル分率\(\displaystyle x_n\)と重量分率\(\displaystyle w_n\)は、それぞれこのような式で与えられます。
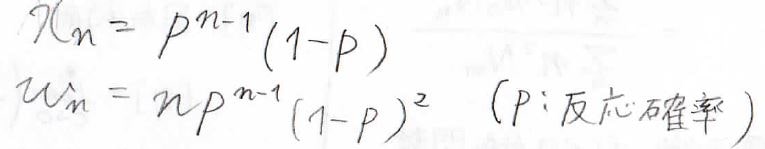
ここで\(\displaystyle p\)は、1回の縮合反応が起こる確率です。
これをグラフで書くと、下のようになります。
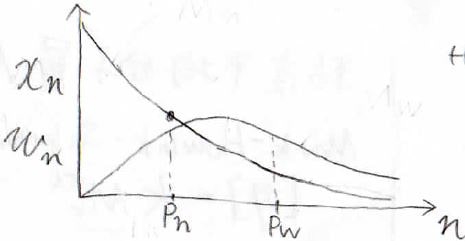
このグラフからわかる重要なことは、数平均重合度と重量平均重合度は必ずしも一致しないということです。
重量平均重合度は高分子量体に大きく影響されるため、分子量分布がある場合、常に\(\displaystyle P_\rm{w}\)は\(\displaystyle P_\rm{n}\)より大きな値になります。
\(\displaystyle P_\rm{n}\)と\(\displaystyle P_\rm{w}\)が一致するのは、単分散、すべての分子が同じ分子量の場合のみになります。
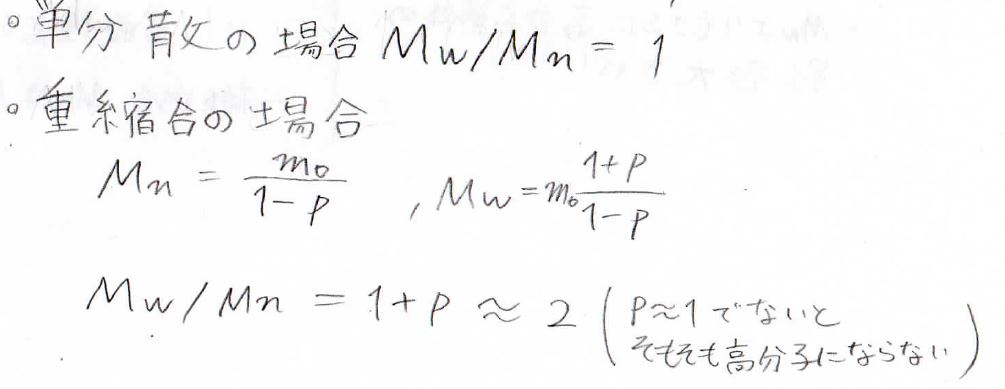
この関係を利用すれば、\(\displaystyle M_\rm{w}\)と\(\displaystyle M_\rm{n}\)の比を分子量分布がどれだけ広いかを表す指標として使うことができます。
\(\displaystyle \frac{M_\rm{w}}{M_\rm{n}}\)が\(\displaystyle 1\)に近いほど、分子量分布が狭いことになります。
重縮合の場合は、\(\displaystyle \frac{M_\rm{w}}{M_\rm{n}}=1+p\)となり、そもそも\(\displaystyle p\)はほとんど\(\displaystyle 1\)でないと高分子は作れないので、\(\displaystyle \frac{M_\rm{w}}{M_\rm{n}}\approx 2\)となります。
\(\displaystyle M_\rm{n}\)、\(\displaystyle M_\rm{w}\)の実験的な求め方
世の中にはいくつもの分子量測定方法がありますが、その測定方法によってどの平均分子量が算出できるのかが変わります。
例えば、\(\displaystyle M_\rm{n}\)は凝固点降下や浸透圧など束一的性質を利用した方法で求めることができます。
中には、平均分子量ではなく分子量分布関数を求める方法もあります。
この場合は、計算によって\(\displaystyle M_\rm{n}\)も\(\displaystyle M_\rm{w}\)も求められるということになります。

いかなる測定にも測定可能な範囲というものがあり、小さすぎる分子、大きすぎる分子は測れません。
例えば、静的光散乱という方法では、\(\displaystyle M_\rm{w}\)が\(\displaystyle 10^4\sim 5\times 10^7\)の範囲になくてはいけません。
ほかの平均分子量
ほかの平均分子量のとり方も紹介しておきます。
高分子を専門とする人の中でも全員が使うわけではないので、\(\displaystyle M_\rm{n}\)や\(\displaystyle M_\rm{w}\)に比べるとマイナーな概念です。
Z平均分子量
1つ目に紹介するのはZ平均分子量です。
これは\(\displaystyle M_\rm{w}\)よりもさらに高分子量体に大きく影響される分子量で、沈降平衡によって測定されるほか、分子量分布から計算によって得られるものです。
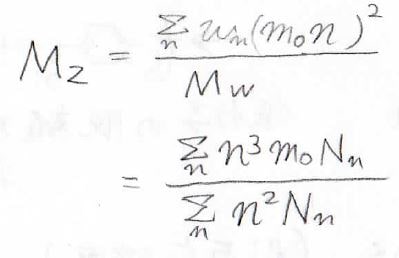
粘度平均分子量
もう1つが粘度平均分子量です。
溶液粘度が分子量に依存するという関係から実験的に求められる分子量です。
ここで用いるのは、Mark-Howink-Sakuradaの式です。
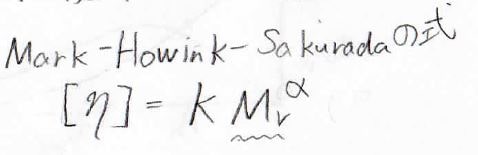
\(\displaystyle [\eta]\)は固有粘度というもので、これは溶液粘度を高分子濃度のビリアル方程式にした際の第2ビリアル係数になります。
定義は、下に示すとおりです。
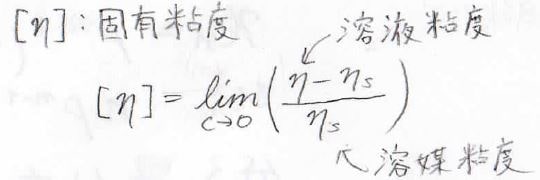
\(\displaystyle \eta_\rm{s}\)が溶媒粘度、\(\displaystyle \eta\)が溶液の粘度、\(\displaystyle c\)が高分子の濃度です。
この粘度平均分子量は経験的に\(\displaystyle M_\rm{w}\)と近い値を示すことが知られています。
分岐構造の多分子性
ここまでは、分子量という視点で多分子性を考えてきましたが、高分子の複雑さは分子量だけでは語れません。
次は、分岐構造について考えていきましょう。
次に示す3つの官能基をもつモノマーから高分子を作ることを考えてみます。

ここで、\(\displaystyle \rm{A}\)と\(\displaystyle \rm{B}\)の間でのみ反応が起こって結合ができるものとします。
まず\(\displaystyle n\)量体の中で、結合を作る\(\displaystyle \rm{B}\)は\(\displaystyle n-1\)個あります。
\(\displaystyle \rm{B}\)は全部で\(\displaystyle 2n\)個あるので、結合を作る\(\displaystyle \rm{B}\)の選び方は\(\displaystyle _{2n}C_{n-1}\)通りになります。
そして、それぞれの\(\displaystyle \rm{B}\)がどの\(\displaystyle \rm{A}\)と反応するのかは、\(\displaystyle B\)の並べ替えを考えればよいので、全部で\(\displaystyle (n-1)!\)通りあることになります。
そして、最後にモノマー単位は互いに区別できないため、\(\displaystyle n!\)で割る必要があります。
これらをまとめると、\(\displaystyle n\)量体の構造異性体の数\(\displaystyle N(n)\)はこうなります。
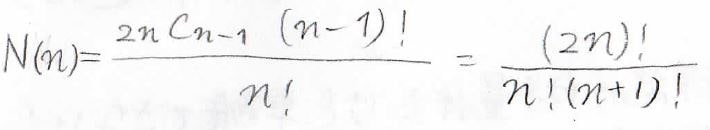
グラフで書くと下のようになり、重合度が大きくなるにつれて、一気に考えうる構造の数が多くなることがわかります。
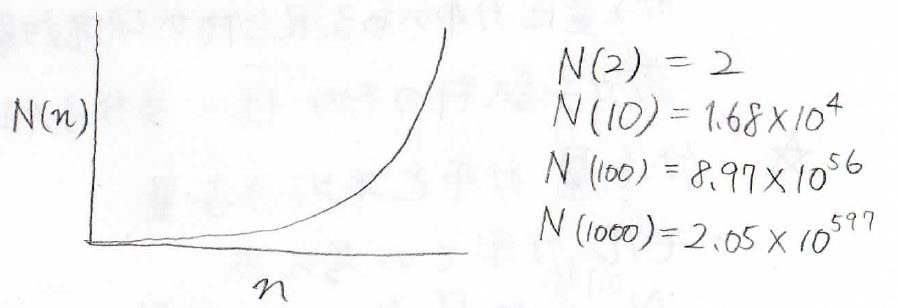
高分子を研究対象にする場合は線状高分子を使う場合が多いのですが、それでも計り知れないほどの異性体があることを考えると、高分子を完全に理解することがいかに難しいかがわかると思います。
共重合体 モノマー配列の多分子性
最後に、共重合体に限った話ではありますが、モノマー配列の多分子性を考えてみましょう。
高分子としては小さめの\(\displaystyle 1000\)量体で、モノマーは2種類、組成比も1:1に固定したとしても考えうるモノマー配列は、\(\displaystyle _{1000}C_{500}\approx 10^{299}\)通りにもなります。
DNAの場合はモノマーが4種類なので、仮に塩基対数が\(\displaystyle 2000\)の場合、考えうる配列はおよそ\(\displaystyle 10^{1204}\)通りにもなります。
DNAはモノマー配列の多分子性を利用することで遺伝情報を保存したり、発現させたりできるというわけです。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




