こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(free energy)
それでは内容に入っていきます！
自発的な変化
まず、クラウジウスの不等式より、自発的なエントロピーの微小変化\(\rm{d}\)\(S\)は必ず\(\rm{d’}\)\(q/T\)以上となります。
ここで\(S\)はエントロピー、\(q\)は系へ与えられた熱量、\(T\)は絶対温度です。
体積が一定かつ、体積変化を伴う仕事もないときには、内部エネルギーの微小変化\(\rm{d}\)\(U\)は\(\rm{d’}\)\(q\)と等しくなるので、\(\rm{d}\)\(S\)は\(\rm{d}\)\(U/T\)以上という関係が成り立ちます。
整理すると、\(\rm{d}\)\(U-T\rm{d}\)\(S\)は必ず\(0\)以下になります。
変化の経路に依存する熱量が消えて、すべてが状態量であることがポイントです。
これは仮に内部エネルギー一定であるときには、エントロピーは一定もしくは増大することを意味します。
また、エントロピーが一定のときには、内部エネルギーは一定もしくは減少することになります。
同様のことを圧力一定条件下についても考えてみましょう。
圧力一定条件で系へ与えられた熱量は、エンタルピー\(H\)の変化量に等しくなります。
これをクラウジウスの不等式に代入すると、\(\rm{d}\)\(S\)は\(\rm{d}\)\(H/T\)以上であることになります。
また\(\rm{d}\)\(H-T\rm{d}\)\(S\)は\(0\)以下です。
そして、エンタルピー一定のときには、エントロピーが一定もしくは増大します。
仮にエントロピー一定のときには、エンタルピーは一定もしくは減少します。
ただここで気をつけたいのは、内部エネルギーとエンタルピー自体が小さくなろうという性質を持っているわけではないということです。
どういうことかというと、まず系のエントロピー変化\(\rm{d}\)\(S_\rm{in}\)\(\)、外界のエントロピー変化を\(\rm{d}\)\(S_\rm{ex}\)\(\)とします。
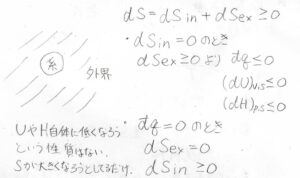
すると、エントロピー増大則より、\(\rm{d}\)\(S_\rm{in}\)\(+\rm{d}\)\(S_\rm{ex}\)\(\)は\(0\)以上となります。
仮に\(\rm{d}\)\(S_\rm{in}\)\(=0\)のときには、\(\rm{d}\)\(S_\rm{ex}\)が\(0\)以上にならなければならず、そのために系から熱を捨てる必要が出てきます。
その結果として内部エネルギーやエンタルピーが減少するというわけです。
反対に内部エネルギーやエンタルピーが一定というのは、\(\rm{d}\)\(S_\rm{ex}\)\(=0\)ということですから、系内のエントロピーが一定になるか増大しないといけなくなります。
ヘルムホルツエネルギーとギブズエネルギーの定義
ここで新しい状態量を定義します。
\(U-TS\)を\(A\)、\(H-TS\)を\(G\)とします。
これらはそれぞれヘルムホルツエネルギー、ギブズエネルギーと呼ばれています。
なぜこんなものを定義するのかというと、まず温度と体積一定とした場合、ヘルムホルツエネルギーの微小変化\(\rm{d}\)\(A\)は\(\rm{d}\)\(U-T\rm{d}\)\(S\)となり、さっき求めたとおり、これは\(0\)以下になります。
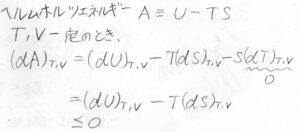
つまり、系に関してヘルムホルツエネルギーの変化量が\(0\)以下になるかどうかを見れば、外界のエントロピーを考えずに、変化の自発性を議論できることになります。
同様に温度と圧力が一定のときには、\(\rm{d}\)\(G\)が\(\rm{d}\)\(H-T\rm{d}\)\(S\)と等しくなるので、\(\rm{d}\)\(G\)が\(0\)以下になるかどうかで変化の自発性がわかるということになります。
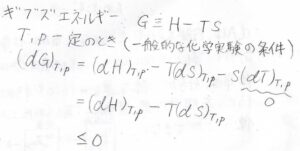
大気の温度と圧力は一定と考えてもあまり問題が起きないので、例えば実験室で何らかの化学反応をさせたといった場合であれば、ヘルムホルツエネルギーでなくてギブズエネルギーで議論されます。
そのため、化学を扱う人はギブズエネルギーの方が見る機会が多いです。
ただ物理実験では、温度と体積一定という条件もあるので、ヘルムホルツエネルギーの方がよく使う人もいます。
最大仕事と自由エネルギー
それで、ヘルムホルツエネルギーには、変化の自発性を考える以外の使い方もあるので紹介します。
使うのは、熱力学第一法則とクラウジウスの不等式です。
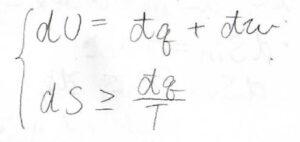
これらを組み合わせると、\(\rm{d}\)\(U\)は\(T\rm{d}\)\(S+\rm{d’}\)\(w\)以上であるという関係が成り立ちます。
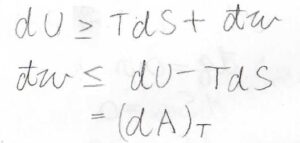
ここで、\(w\)は系へなされた仕事です。
整理すると、\(\rm{d’}\)\(w\)は\(\rm{d}\)\(U-T\rm{d}\)\(S\)以下、つまり温度一定条件での\(\rm{d}\)\(A\)以下となります。
したがって、系になされる最大の仕事は、温度一定条件でのヘルムホルツエネルギー変化と等しいということがいえます。
この系になされる最大の仕事のことは、そのまま最大仕事といいます。
実際の仕事が最大仕事になるのは、可逆であるときです。
最大仕事が内部エネルギー変化より小さくなることを説明すると、つぎのようになります。
まず系のエントロピー変化\(\rm{d}\)\(S_\rm{in}\)\(\)が\(0\)以下のときには、外界のエントロピー変化\(\rm{d}\)\(S_\rm{ex}\)\(\)は\(-\rm{d}\)\(S_\rm{in}\)\(\)以上となり、必ず系から外界へ熱を捨てないといけなくなります。
捨てた熱があるため、最大仕事は必ず内部エネルギーの変化量よりも小さくなるというわけです。
ヘルムホルツエネルギーの変化量\(\rm{d}\)\(A\)は内部エネルギーの変化量のうち、自由に仕事へと変換できる部分だという意味で、ヘルムホルツエネルギーのことは別名、ヘルムホルツ自由エネルギーとも呼ばれます。
この仕事に使うことができない部分とは、ヘルムホルツエネルギー\(U-TS\)のうちの\(TS\)に関係しています。
分子論的に説明すると、系が仕事をするときには、分子が一様な運動をする必要があるのですが、仕事をする前とした後ではいずれも分子の運動はランダムになります。
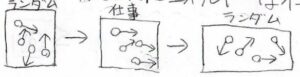
ランダムに分子が動いているとき、系は仕事をしません。
この不規則な分子運動として残ったエネルギーがどうしても仕事に変換することができない部分です。
それで、ギブズエネルギーについても最大仕事的なものがあります。
まず、ギブズエネルギーの微小変化\(\rm{d}\)\(G\)は\(\rm{d}\)\(U+p\rm{d}\)\(V+V\rm{d}\)\(p-T\rm{d}\)\(S-S\rm{d}\)\(T\)となります。
温度と圧力を一定とした場合は、熱力学第一法則も使って\(\rm{d}\)\(G=\rm{d’}\)\(q+\rm{d’}\)\(w+p\rm{d}\)\(V-T\rm{d}\)\(S\)となります。
ここにクラウジウスの不等式を入れると、\(\rm{d}\)\(G\)は\(\rm{d’}\)\(w+p\rm{d}\)\(V\)以上となります。
ここで、膨張の際に系へなされる仕事\(\rm{d’}\)\(w_\rm{expansion}\)\(=-p\rm{d}\)\(V\)となるので、膨張を伴わない仕事\(\rm{d’}\)\(w_\rm{add}\)\(\)は全体の仕事\(\rm{d’}\)\(w\)と\(p\rm{d}\)\(V\)の和になります。
したがって、ギブズエネルギーの変化\(\rm{d}\)\(G\)は、膨張を伴わない仕事の最大量に等しいということになります。
例えば、電池は電子を送り出すポンプとして仕事をするものなので、そういった電気的な仕事が\(\rm{d’}\)\(w_\rm{add}\)\(\)に含まれます。
そして、ギブズエネルギーも、内部エネルギーのうち膨張以外の仕事として変換できる部分を表すものとして、ギブズ自由エネルギーと呼ばれます。
ゴム弾性とギブズエネルギー
それでは最後にゴムを使って、ギブズエネルギーを感覚的にとらえるということをやってみます。
純粋な化学の教科書にはあまり載っていない内容なので、もしよければ、お手元に輪ゴムを用意して実際にやってみてください。
一般的にゴムというものは、高分子が化学結合により永久架橋された網目構造を有していて、綺麗に分子が整列できないので結晶になれず、融点を持たないというおもしろい性質があります。
ガラス転移温度より十分高い温度では、液体と同じように激しく分子運動しているため、容易に変形し、また元の形に戻ることができます。
つまり、ゴムは可逆系です。
ちなみに分子運動は液体と同程度に激しくても、架橋されているために流動できないので、ゴムは結晶ではない固体に分類されます。
ここで、温度一定条件におけるゴムのギブズエネルギーの微小変化\(\rm{d}\)\(G\)は\(\rm{d}\)\(H-T\rm{d}\)\(S+f\rm{d}\)\(L\)と表されます。
可逆系なので、ゴムに与えられた熱量\(\rm{d’}\)\(q\)は\(T\rm{d}\)\(S\)、膨張を伴う仕事\(\rm{d’}\)\(w\)は\(-p\rm{d}\)\(V\)となります。
ここで、\(f\)はゴムが縮む方向を正とした張力、\(L\)はゴムの長さです。
これを張力\(f\)について整理すると、\(f=(\partial H/\partial L)_{T,p}-T(\partial S/\partial L)_{T,p}\)となります。
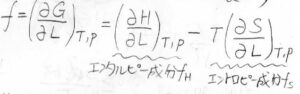
つまり、温度と圧力一定条件下におけるゴムの張力は、エンタルピー由来の成分\(f_H\)とエントロピー由来の成分\(f_S\)に分離されます。
これらは、ゴムの長さ\(L\)に対して異なる依存性をもっており、実際に張力を測定せずとも、ゴムを引っ張った感覚だけでも、分離することができます。
エンタルピー成分
まず、エンタルピー成分の起源は、網目鎖の伸びきりです。
結合長や結合角にひずみがかかると不安定化が起こり、復元力が生まれます。
今は、わかりやすいように書いていますが、実際の結合性軌道のポテンシャルの谷はとてもシャープなので、ひずみに対して爆発的に増大します。
エントロピー成分
対して、エントロピー成分はボルツマンの式から考えることができます。
ボルツマン定数を\(k_\rm{B}\)\(\)、とりうる微視的状態の数を\(W\)としてエントロピーは\(k_B\ln{W}\)と書かれます。
こちらの記事で導出をしています。
仮に、一本の網目鎖について両末端間距離\(R\)を固定することを考えます。
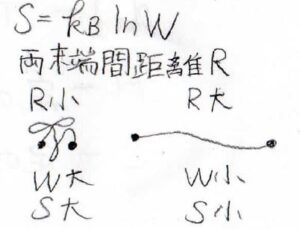
すると、\(R\)がとても小さいときには、鎖が丸まった形をとるので、どういう経路をとるのかという場合の数が多くなり、エントロピーも大きくなります。
\(R\)が大きいときには、経路のとり方の数が少なくなるため、エントロピーも小さくなります。
エントロピーを大きくするために、常に短くなる方向へと復元力が生まれるのがエントロピー成分の起源です。
金属やセラミックなどの材料では、エントロピーの寄与がとても小さいですが、高分子の場合はこれが大きく寄与してきます。
ゴムの長さと全張力の関係
実際にゴムの長さ\(L\)に対して張力fを測定すると、このような逆S字のカーブとなることが知られています。
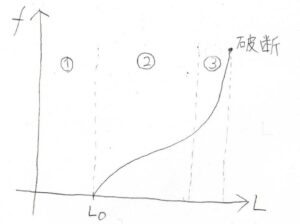
ここでは、①～③の領域に分けて考えていきます。
まず①の領域についてですが、一次元的にはエントロピーを最大化するために常に縮む方向へ復元力がはたらきます。
しかし、実際のゴムは伸長によってほとんど体積が変化しないという性質を持っています。
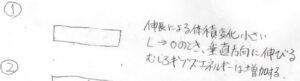
つまりは、伸長した分に伴って、断面積が小さくなっていくわけです。
\(L\)が\(0\)まで縮んだ時には、断面積が\(\infty\)となり、伸長方向から見て垂直な方向についてのエントロピーはむしろ\(-\infty\)になってしまいます。
全体のギブズエネルギーが増加することから、ここまで縮むことは自発的に起こりえないということになり、実際は自然長\(L_0\)で張力\(0\)となります。
②の状態では、網目鎖は両末端間距離が変化しますが、結合角や結合長へのひずみは小さい状態です。
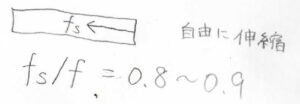
ここではエントロピー弾性が優勢となります。
ゴムの種類に依存しますが、全張力に占めるエントロピー成分の割合は、8~9割程度になります。
そして③の状態、ゴムが破断する寸前で\(f\)が跳ね上がっているのがエンタルピー弾性優勢となっている部分です。
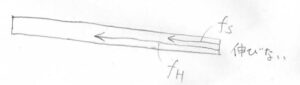
網目鎖はすでに伸びきっているので、結合長や結合角にひずみが生じます。
この領域ではゴムがこれ以上伸びにくくなり、いずれは破断します。
エントロピーは感覚的にとらえるのが難しい状態量で、理解に苦しむ方も多いと思いますが、実際にゴムを引っ張ってみると、エンタルピーとエントロピーの両方を感じることができます。
自由エネルギーの理解にもおすすめです。
ゴム弾性については、こちらの記事でさらに詳しく解説しています。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
