こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(network model)
それでは内容に入っていきます!
アフィン変形
始めに、アフィン変形というものの説明をします。
アフィン変形とは、試料を変形させたときに、試料全体の巨視的な変形量と網目鎖の局所的な変形量が相似になるような変形のことを言います。
例えば、等方的なゴムの試料を\(x\)、\(y\)、\(z\)軸方向にそれぞれ伸長比が\(\lambda_x\)、\(\lambda_y\)、\(\lambda_z\)となる変形を加えたとします。
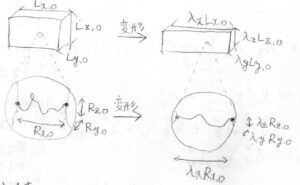
その時に\(1\)本の網目鎖の伸長比も\(\lambda_x\)、\(\lambda_y\)、\(\lambda_z\)となるというのがアフィン変形です。
こうしておけば、網目鎖\(1\)本だけ考えるだけで全体の張力を理論的に計算できるようになります。
補足:ひずみとポアソン比
ここで、ひずみの定義とポアソン比について、改めて説明しておきます。
一般的なゴムでは、引っ張った長さに反比例して断面積は小さくなっていくため、伸長による体積変化はほとんどありません。
体積が一定のとき、\(\lambda_x\lambda_y\lambda_z=1\)が成り立ちます。
ひずみの定義はいくつかあるのですが、ここではコーシーひずみとヘンキーひずみを紹介します。
コーシーひずみは、変形前の長さと変形量の比として定義されます。
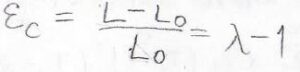
コーシーひずみは別名、工学ひずみとも呼ばれます。
伸長比を使うと\(\lambda-1\)と表されます。
そして、ヘンキーひずみは伸長比の自然対数として定義されます。

こちらは別名、真ひずみ、対数ひずみ、自然ひずみとも呼ばれます。
伸長比を使うと、\(\ln{\lambda}\)となります。
したがって、コーシーひずみ\(\varepsilon_\rm{C}\)とヘンキーひずみ\(\varepsilon\)の関係は、このように書けます。
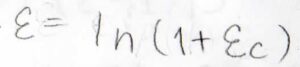
そして例えば、ひずみ速度一定で一軸伸長の実験をしたい場合には、コーシーひずみで考えたほうが感覚的には簡単なのですが、実はヘンキーひずみのほうが計算のときに扱いやすいです。
というのも、コーシーひずみでは加成性が成り立ちません。

一気に引っ張った場合のコーシーひずみと、2段階に分けて引っ張った場合のコーシーひずみの和は一致しないので、変化の過程を考えることができません。
対数にすれば、ひずみの和が真数どうしで約分できるので、うまく変形前と変形後の長さだけで一意的に記述することができます。
ポアソン比は伸長方向についてのヘンキーひずみ\(\varepsilon_\parallel\)と垂直方向へのヘンキーひずみ\(\varepsilon_\perp\)の比にマイナスを付けた値として定義されて、この値で伸長による体積変化がわかります。

体積が変化しないとき、\(\lambda_x\lambda_y\lambda_z=1\)が成立するので、\(x\)軸方向に伸長比\(\lambda\)だけ変形させたときには、\(\displaystyle \lambda_y=\lambda_z=\frac{1}{\sqrt{\lambda}}\)となります。

したがって、このときのポアソン比は\(0.5\)となります。
つまり、ポアソン比が\(0.5\)というのは、試料が伸長により体積変化しないことを意味しています。
ポアソン比は\(-1\)から\(0.5\)までの値をとりますが、負の値をとる材料、すなわち伸長により断面積が大きくなる材料はかなり珍しいです。
アフィンネットワークモデル
続いて、アフィン変形した場合にエントロピー由来の張力がどのような式で表されるのかを求めていきます。
まず、これは前回の復習ですが、温度\(T\)と圧力\(p\)が一定の条件下におけるゴムの張力\(f\)は、エンタルピー由来の成分\(f_H\)とエントロピー由来の成分\(f_S\)に分離することができます。
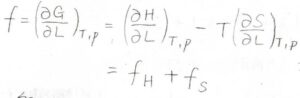
それぞれは結合角や結合長のひずみと網目鎖全体の空間的な構造変化に由来しています。
ゴムは金属やセラミックスなど他の材料とは異なり、エントロピーが応力に大きく寄与しており、破断寸前の大変形領域を除き、全体の張力に対するエントロピー成分の割合は、\(8\sim 9\)割程度になります。
ゴムの張力を簡単に考えるために、エンタルピー成分を\(0\)と近似してしまうこともあります(第一近似)。

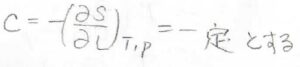
このときには、\(\displaystyle (\frac{\partial S}{\partial L})_{T, p}\)が一定であるとすることで、エントロピー成分は温度に比例することになります。
ネオ-フッキアン(neo-Hookean)モデル
では、伸長によりエントロピー成分はどのように変化するのかを求めていきます。
今回は三次元空間にあるガウス鎖の両末端間距離の分布から導出します。
この式の中で\(P(R)\)は確率密度、\(b_\rm{s}\)はセグメント長、\(N\)はセグメント数です。
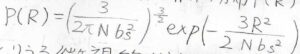
両末端間距離が\(R\)のときのエントロピーを求めるために、とりうる微視的状態の数\(W(R)\)を考えると、これは\(C’P(R)\)となります。
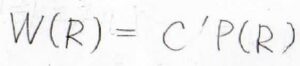
\(P(R)\)は\(0\)から\(1\)までの値をとるので、整数ではありません。
そこですべての\(R\)についてのコンフォメーションの数を考慮した定数\(C’\)をかけて、場合の数としています。
ボルツマンの式を使うと、エントロピーは\(\displaystyle -\frac{3}{2}\frac{k_\rm{B}}{\mathit{Nb}_\rm{s}^2}(\mathit{\lambda_x}^2\mathit{R_{x, 0}}^2+\mathit{\lambda_y}^2\mathit{R_{y, 0}}^2+\mathit{\lambda_z}^2\mathit{R_{z, 0}}^2)\)\(+C^{”}\)と書けます。

ここで、\(k_\rm{B}\)はボルツマン定数、\(C^{”}\)は伸長比に依存しない定数です。
いまは等方的な試料を考えているため、変形前の網目鎖の長さの\(2\)乗、すなわち\(R_{x, 0}^2\)、\(R_{y, 0}^2\)、\(R_{z, 0}^2\)の平均値は、\(\displaystyle \frac{1}{3}Nb_\rm{s}\)\(^2\)と書けます。
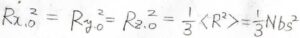
これを代入すると、\(\displaystyle S(R)=-\frac{k_\rm{B}}{2}(\lambda_x^2+\lambda_y^2+\lambda_z^2)+C^{”}\)となります。
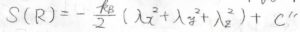
特に、伸長によって体積が変化しない場合は、\(\lambda_x=\lambda\)として\(\displaystyle S(R)=-\frac{k_\rm{B}}{2}(\lambda^2+2/\lambda)\)となります。
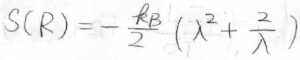
\(\lambda=1\)のときの値を\(S_0’\)とすると、これは\(\displaystyle -\frac{3}{2}k_\rm{B}\)\(+C^{”}\)となります。
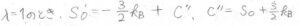
このことより、\(\displaystyle S(R)=-\frac{k_\rm{B}}{2}(\lambda^2+\frac{2}{\lambda}-3)+S_0’\)と書けます。
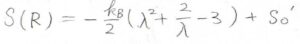
そしてこれは、\(1\)本の網目鎖についてのみ考えたエントロピーだったので、試料全体で考えると、これに網目鎖の本数をかけなければいけません。
網目鎖の数密度を\(\nu\)、試料の体積を\(V\)とすると、\(\displaystyle S(R)=-\frac{\nu Vk_\rm{B}}{2}(\lambda^2+\frac{2}{\lambda}-3)+S_0\)となります。

この式を使うと、張力はすべてエントロピーに由来していると近似したとき、\(\displaystyle f=\frac{\nu Vk_\rm{B}\mathit{T}}{L_{x, 0}}(\lambda-\frac{1}{\lambda^2})\)となります。
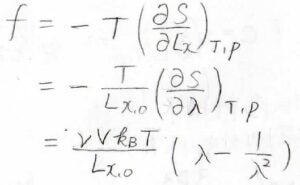
さらに、試料の大きさの情報を排除して、ゴムの内部状態だけを見るために応力で表すと、次のようになります。
まず、変形前の断面積\(L_{y, 0}L_{z, 0}\)で\(f\)を割ると、応力\(\sigma_\rm{nom}\)は\(\nu k_\rm{B}\)\(\displaystyle T(\lambda-\frac{1}{\lambda^2})\)となります。
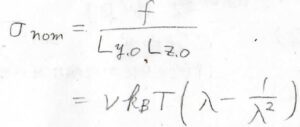
張力を変形前の断面積で割って計算された応力のことは、公称応力と言います。
ただ、厳密にゴムの内部情報を得るためには、変形中の断面積\(L_yL_z\)で割らなければいけません。
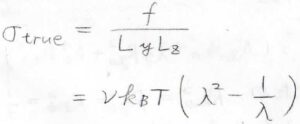
体積変化がないとき、\(L_yL_z=L_{y, 0}L_{z, 0}\lambda\)であるため、\(\sigma_\rm{true}\)\(=\nu k_\rm{B}\)\(\displaystyle T(\lambda^2-\frac{1}{\lambda})\)となります。
このようにして得られる応力を真応力と言います。
実験的には、変形中の断面積を測定するのは困難であるため、公称応力を測定して、ポアソン比から真応力を求めるほうが簡単です。
そして、どちらの応力にもある比例定数\(\nu k_\rm{B}\)\(T\)は弾性率(modulus)と呼んで、\(G\)と表します。
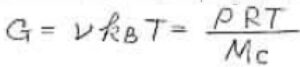
網目鎖の数密度\(\nu\)は試料の密度\(\rho\)にアボガドロ数をかけて、網目鎖の平均モル質量\(M_\rm{c}\)で割った値に等しいため、\(\displaystyle G=\frac{\rho RT}{M_\rm{c}}\)ともかけます。
ただし、この式の中の\(R\)は気体定数を指します。
また、真応力を伸長比で偏微分して、伸長比\(1\)へ極限をとった値は、ヤング率(Young’s modulus)と言って、\(E\)で表されます。
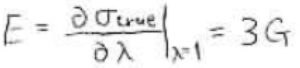
ヤング率は、弾性率とポアソン比など、独立なパラメータ2つを使うと換算することができて、ポアソン比が\(0.5\)のときには\(E=3G\)となります。
ムーニー-リブリン(Mooney-Rivlin)モデル
以上のようにして求めた張力なわけですが、実は、現実のゴム試料の力学的性質を説明するにはまだ不完全です。
先ほどのモデルと、実際の測定結果を重ねると、このようになります。

まず、先のモデルではエンタルピー成分を\(0\)としているため、どこまでも伸びることになります。
よって高伸張領域ではモデルより実験結果のほうが大きな張力となります。
そして、中間領域では逆にモデルのほうが実際より少し大きな張力を予想することになります。
ここからは、この実際の結果を現象論的にどのように扱うのかという話をしていきます。
まず、各方向についての伸長比\(\lambda_x\)、\(\lambda_y\)、\(\lambda_z\)から、座標系によらない3つの不変量\(I_1\)、\(I_2\)、\(I_3\)を作ります。
それぞれの定義は次のとおりです。
\(I_1=\lambda_x^2+\lambda_y^2+\lambda_z^2\)
\(I_2=\lambda_x^2\lambda_y^2+\lambda_y^2\lambda_z^2+\lambda_z^2\lambda_x^2\)
\(I_3=\lambda_x^2\lambda_y^2\lambda_z^2\)
それぞれの物理的な意味としては、\(I_1\)がひずみの総量、\(I_2\)が異なる方向へのひずみ同士の相関、\(I_3\)が体積の変化を反映したパラメータとなっています。
そして、あらゆる材料について、伸長による単位体積あたりの自由エネルギー変化\(\displaystyle \frac{\Delta F}{V}\)は、このような級数で表せると考えます。

単位体積あたりのエネルギーの単位は\(\rm{J\ m}\)\(^{-3}\)なので、\(\rm{Pa}\)になります。
\(C_1\)以外がすべて\(0\)となったものは、前節で考えていたモデルとまったく同じになります。
この式に従う材料のことを、ネオ-フッキアン(neo-Hookean)固体、もしくは理想弾性体と言います。
フック弾性体といえばバネですが、それを体積一定として三次元的に考えたものだということで、「ネオ」と付きます。
そして、中間の伸長域でneo-Hookeanの式が実際よりも大きな張力となったとき、その補正として\(C_1\)と\(C_2\)以外がすべて\(0\)となることを考えます。
この式をムーニー-リブリン(Mooney-Rivlin)の式と言って、これに従う材料をMooney-Rivlin固体と言います。
試料の体積は変化しないものとして、Hookの式、neo-Hookeanの式、Mooney-Rivlinの式を重ねて書くと、このようになります。
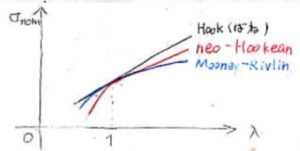
縦軸が公称応力、横軸が一軸伸長試験における伸長比です。
Mooney-Rivlinの式では、応力の第一項が\(\displaystyle \lambda-\frac{1}{\lambda^2}\)、第二項が\(\displaystyle 1-\frac{1}{\lambda^3}\)に比例することになります。
これにより、neo-Hookeanの式より伸長比依存性が小さくなります。
より高次の項も考慮すれば、実際のゴムの測定結果にうまく合わせることができます。
高伸長比領域における鎖の伸びきりも考えることが可能です。
ジェント(Gent)モデル
また、ひずみの最大量を決めることで、そこで発散するような関数を作る考え方もあります。
その例が、ジェント(Gent)モデルです。

\(I_\rm{m}\)が\(I_1\)の最大量で、\(I_1=I_\rm{m}\)のときに自由エネルギーが発散します。
\(I_\rm{m}\)を無限大としたときには、neo-Hookeanの式になります。
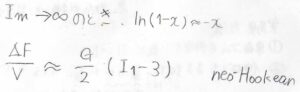
ファントムネットワークモデル
これまではアフィン変形するネットワークとして考えてきたわけですが、それだと現実よりも大きな応力を予想してしまうことがあります。
問題は、試料の変形量に比例して、網目鎖の両末端も変形し、位置がその場で固定されると考えていることにあります。
ゴムは固体ですが、分子運動は液体と同程度に激しいため、架橋点の位置に熱的な揺らぎを考えたほうが現実に近いです。
ということで、ここからは架橋点の熱的な揺らぎを考慮したファントムネットワークモデルの話をしていきます。
まず、固定された材料表面のある位置\(\boldsymbol{r}_0\)に結合し、もう一方の末端の位置が\(\boldsymbol{r}\)の高分子鎖を考えます。
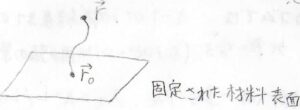
こちらの末端は固定されておらず、ランダムに熱運動しています。
このとき、\(\boldsymbol{r}\)の分布は\(\displaystyle \exp{[-\frac{3(\boldsymbol{r}-\boldsymbol{r}_0)^2}{2Nb_\rm{s}^2}]}\)に比例します。
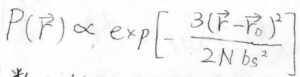
ここで、試料表面から\(\boldsymbol{r}\)の位置まで繋がれた高分子鎖が\(1\)本ではなくて、\(n\)本あった場合も考えてみます。
それぞれの鎖が材料表面と結合している位置を\(\boldsymbol{r}_i\)とすると、\(\boldsymbol{r}\)の分布はそれぞれの鎖\(1\)本についての分布をすべてかけたものになるので、指数の和の形にするとこのようになります。
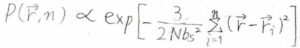
ここで、材料表面の結合点の平均を\(\langle \boldsymbol{r}_0 \rangle\)とおきます。

また、材料表面から見て、架橋点が十分に離れていたときには、個々の結合位置の違いが分布にあまり影響しなくなります。
したがって、平均のパラメータだけを使って架橋点の位置の分布を表すことができます。
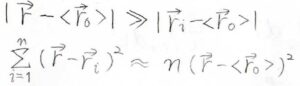
このような考え方を平均場近似といって、物理化学では本当によく出てくる考え方なので言葉だけでも知っておいてください。
この分布をよく見てみると、これはセグメント数が\(\displaystyle \frac{N}{n}\)になっただけで、それ以外は鎖\(1\)本の式とまったく同じ形になっています。
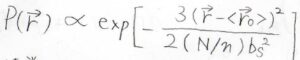
つまり、架橋点に繋がれた鎖の本数が多いほど、架橋点は材料表面に近いところに集中しやすくなり、それは、セグメント数\(\displaystyle \frac{N}{n}\)の短い鎖\(1\)本の末端として考えることができます。
ここで、仮に架橋点の分岐度を\(f\)として、材料表面に結合した\(f-1\)本の鎖に繋がれた架橋点\(\rm{A}\)とそこからさらに繋がれた架橋点\(\rm{B}\)を考えます。
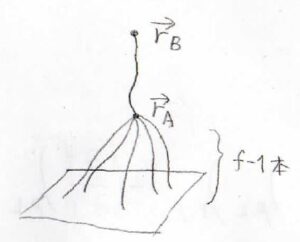
すると、架橋点\(\rm{B}\)に繋がった仮想的な\(1\)本の鎖のセグメント数は、\(\displaystyle N+\frac{N}{f-1}\)となります。
これがまた\(f-1\)本あるなら、\(\displaystyle \frac{N+N/(f-1)}{f-1}\)となります。
これを\(N\)でくくると、\(\displaystyle N[\frac{1}{f-1}+\frac{1}{(f-1)^2}]\)となり、架橋点\(\displaystyle \rm{A}\)の式に二次の項が追加された形になります。
これを何度も繰り返していくと、このような無限級数として考えることができるので、固定された材料表面から十分に離れたある架橋点について、考えられる仮想的な鎖\(1\)本のセグメント数は\(\displaystyle \frac{N}{f-2}\)となります。

アフィンネットワークでは、両末端が固定された鎖を考えていることになるのですが、それはこのように直列につないだ鎖として考えることができます。
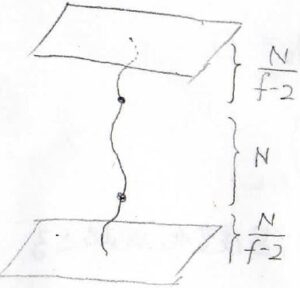
そのセグメント数は\(\displaystyle N+\frac{2N}{f-2}=\frac{Nf}{f-2}\)となります。
つまり、熱的な揺らぎを考えた場合の実効のセグメント数は、実際の\(\displaystyle \frac{f}{f-2}\)倍となります。
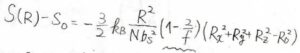
これは網目鎖の数密度が小さくなるということなので、ファントムネットワークモデルの弾性率は、アフィンネットワークモデルの値の\(\displaystyle 1-\frac{2}{f}\)倍となります。
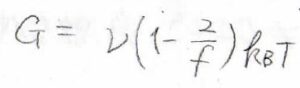
仮に架橋点の分岐度が\(4\)のときには、弾性率が\(\displaystyle \frac{1}{2}\)倍になるので、架橋点の位置の揺らぎは弾性率に大きな影響を及ぼしうると言えます。
今回は、ガラス転移温度より十分に高い温度において、化学架橋された純粋なゴムに限ってお話ししました。
モデルの中で必要な情報は、網目の密度や分岐度だけで、化学的な構造はまったく反映されていません。
しかし、実際のゴム製品では、複数のモノマーを共重合して嵩高さを変化させることで、ガラス転移温度を調整したり、シリカゲルなどの微粒子を混ぜることで力学特性を変えたりするので、もっといろいろな要素を考えなくてはいけないことが多いです。
また、溶媒を含ませたときの物性も重要な研究対象です。
そして、絡み合いや会合によって形成された物理的なネットワークでは、平衡定数や、濃度依存性、高分子の剛直性なども影響してくるので、高分子ネットワークについてはまたの機会に扱っていこうと思います。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!