こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Debye-Huchel)
それでは内容に入っていきます!
平均活量係数
まず、\(\rm{AB}\)という塩が溶解して\(\rm{A^+}\)というカチオンと\(\rm{B^-}\)というアニオンに電離したという場合を考えてみます。

1つの分子でカチオンとアニオンが1つずつである塩を\(1,1-\)電解質と言います。
それぞれのイオンについて、化学ポテンシャル\(\mu\)は、理想溶液の値\(\mu^\rm{ideal}\)から\(RT \ln{\gamma}\)だけ変化した値として書けます。
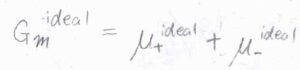
ここで、\(R\)は気体定数、\(T\)は絶対温度、\(\gamma\)は活量係数です。
このことより、イオンの全モルギブズエネルギー\(G_\rm{m}\)は理想溶液の値\(G_\rm{m}\)\(^\rm{ideal}\)から\(RT \ln{(\gamma_+\gamma_-)}\)変化した値になります。
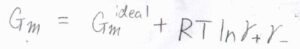
ここで平均活量係数\(\bar{\gamma}\)というものを考えます。
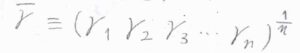
平均といっても、これは一般的に使われる相加平均ではなく、幾何平均です。
つまり、溶液中に存在するすべてのイオンについて、活量係数の和ではなく積をとります。
そして、イオンの数を\(n\)として、その積の\(n\)乗根をとるという方法です。
\(1,1-\)電解質の場合は、\(\displaystyle (\gamma_+ \gamma_-)^\frac{1}{2}\)を平均活量係数\(\gamma_\pm\)とします。
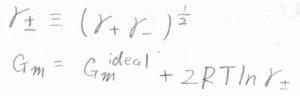
すると、\(G_\rm{m}\)\(=G_\rm{m}\)\(^\rm{ideal}+2RT \ln{\gamma_\pm}\)となります。
仮に、塩が\(p,q-\)電解質だった場合は、\(G_\rm{m}\)\(=G_\rm{m}\)\(^\rm{ideal}\)\(+(p+q)RT \ln{\gamma_\pm}\)となります。
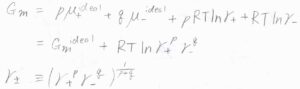
ここで、\(\gamma_\pm=(\gamma_+^p \gamma_-^q)^\frac{1}{p+q}\)です。
仮に、すべてのイオンの活量係数が等しく、平均活量係数で表せるときには、\(\mu_+=\mu_+^\rm{ideal}\)\(+RT \ln{\gamma_\pm}\)、\(\mu_-=\mu_-^\rm{ideal}\)\(+RT \ln{\gamma_\pm}\)となります。
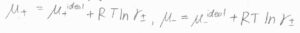
この状態を、非理想性が均等に分配されていると言います。
静電引力、斥力は遠距離力であり、同じく遠距離力である重力と比べてもはるかに大きな力になります。
また、誘起双極子にはたらくファンデルワールス力よりも大きいです。
したがって、電解質の溶液では、当然ながら溶媒和もあるのですが、イオン間の相互作用が大きく非理想性に寄与していると考えることができます。
先ほどの非理想性の等分配とは、つまりイオン間の静電的な相互作用のみによって活量係数が決まっているような状態だと考えてください。
デバイ-ヒュッケルの極限法則
デバイ-ヒュッケル理論という理論では、次のようなモデルでイオンの活量係数を求めています。

まず、1つのイオンに着目します。
この図では、カチオンとしていますが、着目するのはアニオンでも構いません。
このイオンの周りでは、静電引力によって逆符号の電荷をもつイオンが引き寄せられて、静電斥力により同符号の電荷をもつイオンは離れようとします。
その結果、局所的に1つのイオンの周りで、逆符号の電荷をもつイオンの濃度が高くなると考えられます。
デバイ-ヒュッケル理論では、これを単体問題になるように粗視化して、周囲のイオンをもやのように広がった電荷として考えます。
これをイオン雰囲気と言います。
反対の電荷をもつイオンが周囲にあると、中心にあるイオンの電荷が見かけ上小さくなります。
この現象を静電遮蔽と言います。
これにより、イオンの実効濃度が実際の濃度よりも低くなるということです。
このモデルから、次に示すデバイ-ヒュッケルの極限法則というものが導かれます。
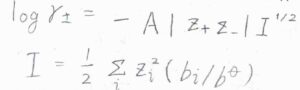
\(\gamma_\pm\)の常用対数\(\log{\gamma_\pm}\)は、\(-A|z_+z_-|I^\frac{1}{2}\)となります。
ここで、\(A\)は溶媒の種類と温度によって決まる定数で、\(z\)はイオンの価数ですが、アニオンについてはマイナスになるようにとったものです。
標準質量モル濃度を\(1\ \rm{mol\ kg}\)\(^{-1}\)とした場合、\(25^\circ \rm{C}\)の水溶液で\(A=0.509\)という値になります。
\(I\)はイオン強度というパラメータで、上のように定義されます。
\(b\)は質量モル濃度です。
仮に\(z\)の指数が\(2\)ではなく\(1\)だった場合には、電気的中性により\(0\)となるため、これは価数の加重平均とみることができます。
モル濃度を\(c\)として、\(\displaystyle I=\frac{1}{2}\sum_iz_i^2c_i\)とすることもありますが、質量モル濃度のときと単位が違いますので、扱いには注意が必要です。
このモデルでは、イオンの排除体積は考えておらず、また沈殿するようなケースも考えていません。
極限法則の極限とは、イオンの濃度が低いところでのみ成り立つという意味です。
こちらに示した拡張デバイ-ヒュッケル則やデービスの式は、より濃度が高い領域でも成り立つように提案されたものです。
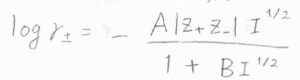
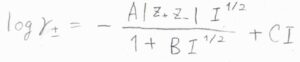
ここで、\(B\)と\(C\)は無次元の定数です。
電気的な仕事
ここからは、デバイ-ヒュッケル理論の説明を順番にしていきます。
まずは、活量係数をどのように求めるのかという話です。
ここで、溶質は\(p,q-\)電解質として考えていきます。
始めに、これらのイオンの電荷がない状態を考えます。
つまり、もとの溶質\(1\ \rm{mol}\)を溶解させると、それが\((p+q)\ \rm{mol}\)の電気的に中性な分子に分かれたとします。
いま、分子間相互作用は静電相互作用しか考えないことにしているため、このままであれば理想溶液になります。
この状態から、イオンに電荷を加えるためには、電子を動かすためのエネルギーが必要となります。
そのために系に与えた溶質\(1\ \rm{mol}\)あたりの仕事を\(w_\rm{e}\)とすると、それはイオン溶液のモルギブズエネルギー\(G_\rm{m}\)と理想溶液のモルギブズエネルギー\(G_\rm{m}\)\(^\rm{ideal}\)の差となります。
化学ポテンシャル\(\mu\)を使うと、このようになります。
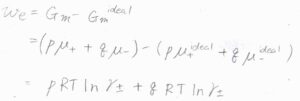
\(\mu-\mu^\rm{ideal}\)\(=RT\ln{\gamma}\)であるため、\(w_\rm{e}\)\(=pRT\ln{\gamma_+}+qRT\ln{\gamma_-}\)となります。
非理想性が均等に分配されているとして、これを整理すると、\(\displaystyle \ln{\gamma_\pm}=\frac{w_\rm{e}}{(p+q)RT}\)となります。
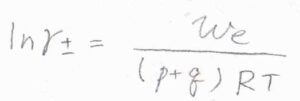
したがって、仕事を求めることができれば、活量係数もわかることになります。
静電遮蔽
次に、静電遮蔽を考えた結論を先にお話しします。
周りのイオンの存在により遠距離まで影響を及ぼしにくくなります。
つまりクーロンポテンシャルの距離依存性が見かけ上大きくなり、より短い距離で\(0\)に近い値になります。
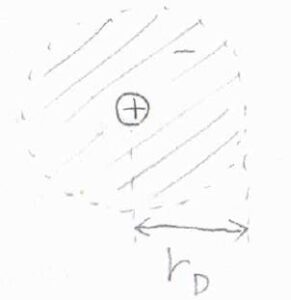
静電遮蔽を考慮したクーロンポテンシャルは、遮蔽クーロンポテンシャルと呼ばれ、こちらの式のようになります。
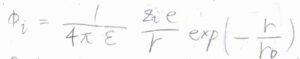
\(\displaystyle \frac{1}{4\pi \varepsilon}\frac{z_ie}{r}\)の部分は、遮蔽が起こっていないときのクーロンポテンシャルであり、これに\(\displaystyle \exp{(-\frac{r}{r_\rm{D}})}\)がかかっています。
\(r_\rm{D}\)はデバイ長と呼ばれ、長さの単位をもつパラメータです。
中心イオンの影響が及ぶ距離の目安になります。
このデバイ長が短いほど、遮蔽の影響が大きく、遠距離にあるイオンと相互作用できなくなります。
横軸をイオンからの距離\(r\)、縦軸をクーロンポテンシャル\(\phi (r)\)の絶対値としてグラフを書くと、下のようになります。
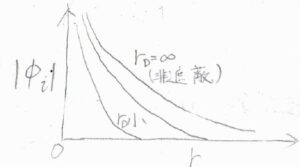
遮蔽がない、つまり\(r_\rm{D}\)\(=\infty\)のときに比べて、\(r_\rm{D}\)が小さいときには、クーロンポテンシャルがより急激に\(0\)に近づくことになります。
通常\(r_\rm{D}\)は、\(\rm{nm}\)スケールの値になるので、精度よく決定したいときには両対数グラフにした方が使い勝手がよくなります。
実際に、任意の長さパラメータ\(a\)を決めて、横軸を\(\displaystyle \log{(\frac{r}{a})}\)、縦軸を\(\displaystyle \log{(\frac{\phi_i}{\phi_i^\rm{ideal}})}\)としてグラフを書くと、下の図のようになります。
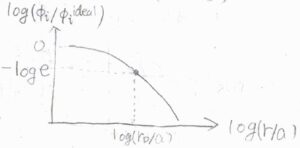
\(r\lt r_\rm{D}\)のときには、遮蔽クーロンポテンシャルは非遮蔽のものと大差がないため、縦軸は\(\log{1}\)、つまり\(0\)になります。
\(r=r_\rm{D}\)となったとき、縦軸は\(-\log{\rm{e}}\)となり、これ以降は両者の差がより拡大していくことになります。
デバイ長とは、遮蔽クーロンポテンシャルが非遮蔽のクーロンポテンシャルの\(\displaystyle \frac{1}{\rm{e}}\)倍になるときの距離にあたります。
遮蔽クーロンポテンシャル
それではなぜ、遮蔽で指数関数をかけるのか、その導出過程についてお話しします。
中心イオン\(i\)の電荷を\(z_i e\)、その電荷密度は\(z_ie\delta(r)\)とします。
ここで\(\delta(r)\)は、ディラックのデルタ関数であり、これで点電荷を表現しています。

いま、水溶液中のある位置にイオンを置いて、平衡状態になるまで放置したとします。
その間の溶液中の対イオンの数密度の変化を\(\Delta \rho_j(r)\)、中心イオンの遮蔽クーロンポテンシャルを\(\phi(r)\)とします。
\(j\)は、イオンの種類を区別するための添え字です。
マクスウェル方程式の1つ、ガウスの法則より、\(\displaystyle \boldsymbol{\nabla} \cdot \boldsymbol{E}=\frac{\rho}{\varepsilon}\)となります。
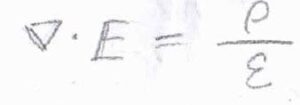
\(\boldsymbol{E}\)は電場、\(\rho\)は電荷密度です。
\(\boldsymbol{E}=-\boldsymbol{\nabla} \phi (r)\)であるため、\(-\boldsymbol{\nabla}\)\(\displaystyle ^2 \phi(r)=\frac{1}{\varepsilon}[z_ie\delta(r)-\Sigma_j z_je\Delta \rho_j]\)となります。
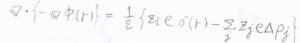
ここで、デバイ-ヒュッケル近似という近似を使います。
まず、系が十分に高い温度であり、それぞれのイオンはボルツマン分布に従っていると考えます。
さらに、濃度が低いために、指数部分をテイラー展開したときに第二項までで近似できるものとします。
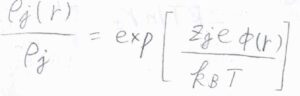
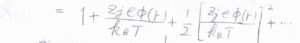
すると、\(\displaystyle \Delta \rho_j(r)=\frac{z_je\rho_j \phi(r)}{k_\rm{B}\mathit{T}}\)となります。
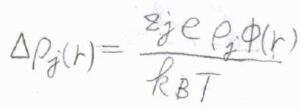
ここで、\(\rho_j\)は溶液全体のイオンの数密度です。
ここから式を簡単にするために、\(\displaystyle \sum_j\frac{\rho_jz_j^2e^2}{\varepsilon k_\rm{B}\mathit{T}}\)を\(k_0^2\)とおきます。
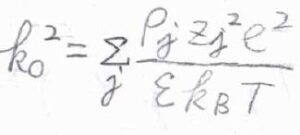
そうして整理すると、\(\displaystyle (\boldsymbol{\nabla}^2-k_0^2)\phi(r)=-\frac{z_ie\delta(r)}{\varepsilon}\)という式が得られます。
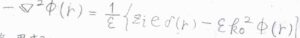
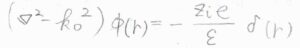
これが遮蔽されたポワソン方程式です。
極座標での\(\boldsymbol{\nabla}^2\)を考えると、\(\displaystyle [\frac{\partial ^2}{\partial r^2}+\frac{2}{r}\frac{\partial}{\partial r}-k_0^2]\phi(r)=-\frac{z_ie\delta(r)}{\varepsilon}\)となります。
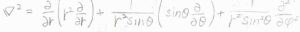
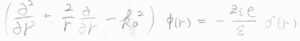
\(r \gt 0\)については右辺が\(0\)となり、この形の微分方程式の一般解は\(C_1\)、\(C_2\)を定数として、\(\displaystyle \frac{C_1}{r}\exp{(-k_0r)}+\frac{C_2}{r}\exp{(k_0r)}\)で与えられます。

いま、\(k_0\)は正の値であり、第二項は\(r\)が大きいときに無限大に発散します。
これは、クーロンポテンシャルの性質と異なるため、\(C_2=0\)となります。
そして、非遮蔽のときには、イオンの数密度\(\rho_j\)をすべて\(0\)に近づけていった極限として考えます。
このとき、\(\displaystyle \phi(r)=\frac{1}{4\pi \varepsilon}\frac{z_ie}{r}\)であり、\(\exp{(-k_0r)}\)は\(1\)に近い値であることから、\(\displaystyle C_1=\frac{z_ie}{4\pi \varepsilon}\)となることがわかります。
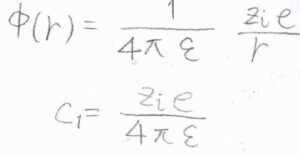
\(k_0\)の逆数をデバイ長\(r_\rm{D}\)とすれば、遮蔽クーロンポテンシャルの式が導かれます。
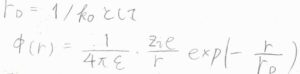
デバイ長とイオン強度
ここからは活量係数を求めていきます。
そのために、デバイ長について、再度考えてみます。
まずイオン\(i\)から\(r\)だけ離れた位置の電荷密度を\(\rho(r)\)とすると、デバイヒュッケル近似より、\(\displaystyle \sum_jz_je\rho_j-\sum_j \rho_j\frac{Z_j^2e\phi_i(r)}{k_\rm{B}\mathit{T}}\)と表されます。

第一項は、溶液全体の電気的中性より\(0\)になります。
そして、第二項をイオン強度\(I\)を用いて表すために、まずは数密度\(\rho_j\)をモル濃度\(c_j\)に変換します。
アボガドロ数\(N_\rm{A}\)を使って、\(\rho_j=N_\rm{A}\)\(c_j\)とします。
また、\(N_\rm{A}\)\(e\)をファラデー定数\(F\)、\(N_\rm{A}\)\(k_\rm{B}\)を気体定数\(R\)と書き換えると、イオンの数密度\(\displaystyle \rho(r)=-\sum_jc_jz_j^2\frac{F^2\phi_i(r)}{RT}\)となります。
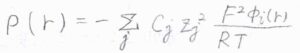
ここから、質量モル濃度\(b_j\)を使って、さらにイオン強度\(I\)で書き換えます。
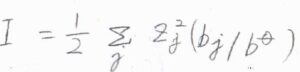
溶液の密度を\(\rho’\)とすると、\(c_j=b_j \rho’\)なので、\(\displaystyle \rho(r)=-\frac{2Ib^\circ \rho’F^2\phi_i(r)}{RT}\)と書けます。
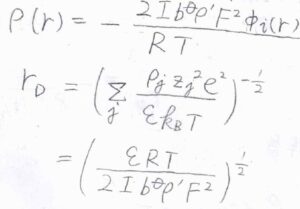
イオン強度を使うことで、\(\sum\)がなくなった形にすることができました。
これと同様に、デバイ長\(r_\rm{D}\)もイオン強度を使うと、\(\displaystyle (\frac{\varepsilon RT}{2Ib^\circ \rho’ F^2})^\frac{1}{2}\)と表すことができます。
活量係数
最後に活量係数を仕事から求めます。
イオン雰囲気由来のクーロンポテンシャルの成分を\(\phi_\rm{atmosphere}\)\(_{, i}(r)\)とすると、これは\(\phi_(r)\)から中心イオン由来のクーロンポテンシャル\(\phi_\rm{central\ ion}\)\(_{, i}(r)\)を引いた値となります。

デバイ長を使って表すと、\(\displaystyle \frac{1}{4\pi \varepsilon}\frac{z_ie}{r}[\exp{(-\frac{r}{r_\rm{D}})}-1]\)となります。
ここで、\(r\)を\(0\)に近づけていったときの極限、つまり中心イオンの位置におけるイオン雰囲気の寄与を考えます。
すると、\(\displaystyle \frac{[\exp{(-r/r_\rm{D}})-1]}{r}\)の部分が\(\displaystyle -\frac{1}{r_\rm{D}}\)に収束するので、\(\displaystyle \phi_\rm{atmosphere}\)\(_{, i}(0)=-\frac{1}{4\pi \varepsilon}\frac{z_ie}{r_\rm{D}}\)となります。
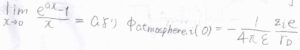
つまり、イオン雰囲気は中心イオンの位置において、\(r_\rm{D}\)だけ離れた位置にある点電荷と同等の作用を及ぼしているということです。
ここから、溶質に電荷を与えるために必要な仕事を求めることができます。
中心イオンの電荷を\(Q\)として、いま\(r_\rm{D}\)は\(Q=z_ie\)のときの値で定数であるとします。
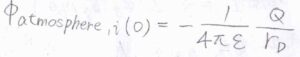
つまり、\(\phi_\rm{atmosphere}\)\(\displaystyle _{, i}(0)=-\frac{1}{4\pi \varepsilon}\frac{Q}{r_\rm{D}}\)です。
\(Q\)を\(0\)から\(z_ie\)まで変化させたとして、それに必要な\(1\ \rm{mol}\)あたりの仕事\(w_\rm{e}\)\(_{, i}\)は、こちらのような定積分で求めることができます。

したがって、\(w_\rm{e}\)\(\displaystyle _{, i}=-\frac{z_i^2F^2}{(8\pi N_\rm{A}\varepsilon \mathit{r}_D}\)となります。
これは1種類のイオンだけに着目した結果ですが、\(p,q-\)電解質\(1\ \rm{mol}\)あたりで考えた仕事\(w_\rm{e}\)は、\(\displaystyle -\frac{F^2(pz_+^2+qz_-^2)}{8\pi N_\rm{A} \varepsilon \mathit{r}_D}\)となります。
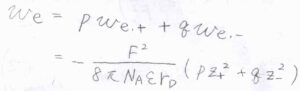
溶液全体では電気的に中性となることより、\(pz_++qz_-=0\)であるため、ここから\(pz_+^2+qz_-^2=-(p+q)z_+z_-\)と変形できます。
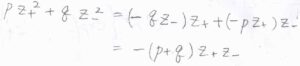
序盤にお話ししたとおり、\(w_\rm{e}\)\(=(p+q)RT\ln{\gamma_\pm}\)であるため、ここから平均活量係数\(\gamma_\pm\)を求められます。
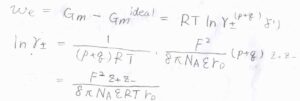
すると、\(\displaystyle \ln{\gamma_\pm}=\frac{F^2z_+z_-}{8\pi N_\rm{A} \varepsilon \mathit{RTr}_\rm{D}}\)となります。
いま、\(z_-\)は負の値となるようなとり方をしているので、\(z_+z_-\)も負の値となります。
したがって、絶対値を使うと、\(z_+z_-=-|z_+z_-|\)と表すことができます。
最後にイオン強度を用いたデバイ長の式を代入します。

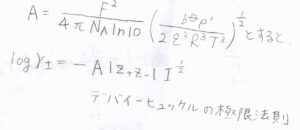
すると、デバイ-ヒュッケルの極限法則の式が導かれます。
無次元量である\(A\)は、\(\displaystyle \frac{F^2}{4\pi N_\rm{A} \ln{10}}(\frac{b^\circ \rho’}{2\varepsilon^3R^3T^3})^\frac{1}{2}\)であり、温度、密度、標準質量モル濃度によって決まる定数です。
低濃度で考えているので、溶液の密度は溶媒の密度とほとんど同じです。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




