こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(activity)
それでは内容に入っていきます！
理想溶液
まずは、理想溶液について復習しましょう。
理想溶液とは、溶液中にあるすべての成分について、どんな組成であっても常にラウールの法則が成立する溶液を指します。
ラウールの法則とは、混合系中のある成分\(i\)の蒸気圧\(p_i\)がモル分率\(x_i\)に比例するというものです。
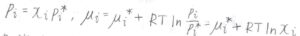
式の中で\(p_i^\ast\)は、純粋なときの飽和蒸気圧を指します。
混合する前と後で、分子同士の相互作用に変化がないときにこの法則が成り立ちます。
ラウールの法則が成り立つとき、化学ポテンシャル\(\mu_i\)は\(\mu_i^\ast+RT\ln{x_i}\)と書けます。
ただし、\(\mu_i^\ast\)は純粋なときの化学ポテンシャル、\(R\)は気体定数、\(T\)は絶対温度です。
実在溶液の活量を用いた表現
そして、実在溶液の化学ポテンシャルの式は、これよりも複雑な形になるのですが、これを理想溶液と同じ式の形で書くことを考えます。
つまり、\(\mu_i=\mu_i^\ast+RT\ln{a_i}\)とします。
\(a_i\)は、実在溶液における実効のモル分率を指し、これを活量と呼びます。
活量は、\(x_i\)に非理想性のパラメータ\(\gamma_i\)をかけたものとして考えます。
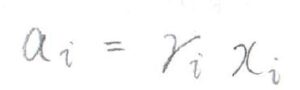
\(\gamma_i\)は\(0\)から\(1\)までの値をとり、これを活量係数と呼びます。
一般的に、活量係数は定数にはならず、モル分率によって変化します。
実在気体のフガシティ―を用いた表現
実は、これと似たような考え方は、以前の記事で一度だけ出てきています。
それは、実在気体の単成分系を考えたときです。
実行の圧力をフガシティーと呼び、\(f\)と表すことにして、モルギブズエネルギーの圧力依存性をこちらの式のように表しました。
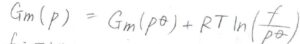
ここでも非理想性のパラメータ\(\phi\)を使って、\(f=\phi p\)としていました。
\(\phi\)はフガシティ―係数と呼ばれ、一般的にこれ自体も圧力に依存することになります。
こんな感じで、複雑な系を考えるときには、理想系の式に実効の値を入れることで式の形はそのままにするということがよくあります。
溶媒の活量係数
それではここから、活量係数がモル分率によってどのような変化をするのかを考えていきましょう。
まず、2成分混合系において、モル分率が多い方の成分を溶媒と呼ぶことにします。
ここでは、溶媒を成分\(\rm{A}\)\(\)とします。
その化学ポテンシャル\(\mu_\rm{A}\)\(\)は\(\mu_\rm{A}\)\(^\ast+RT\ln{x_\rm{A}}\)\(+RT\ln{\gamma_\rm{A}}\)となります。
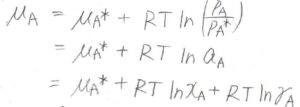
\(\mu_\rm{A}\)\(^\ast+RT\ln{x_\rm{A}}\)はラウールの法則が成り立つときの化学ポテンシャルなので、\(RT\ln{\gamma_\rm{A}}\)が理想系からのずれを表しています。
活量\(a_\rm{A}\)\(\)は\(p_\rm{A}\)\(/p_\rm{A}\)\(^\ast\)と等しく、また定義より\(\gamma_\rm{A}\)\(x_\rm{A}\)\(\)と書けます。
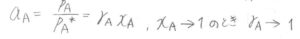
どんな溶液でも、溶媒のモル分率が\(1\)に近いときには、ラウールの法則が成り立つという実験的な事実から、\(x_\rm{A}\)\(\)を\(1\)に近づけていったときには、\(a_A\)と\(x_A\)は近い値となっていきます。
つまり、\(\gamma_A\)は\(1\)に近づいていくということになります。
溶質の活量係数
続いて、溶質について考えていきます。
ここでは、成分\(\rm{B}\)\(\)ということにします。
始めにヘンリーの法則が成り立つ理想希薄溶液を考えます。
ヘンリーの法則とは、混合物中におけるその成分の蒸気圧\(p_\rm{B}\)\(\)がモル分率\(x_\rm{B}\)\(\)と相互作用の変化を反映した圧力と同じ次元のパラメータ\(K_\rm{B}\)\(\)の積で表せるというものです。
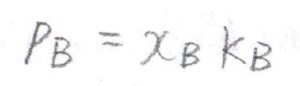
\(K_\rm{B}\)\(\)は純粋なときの飽和蒸気圧とは異なる値であり、溶媒の化学種に依存します。
\(K_\rm{B}\)\(\)を用いると、溶質の化学ポテンシャル\(\mu_\rm{B}\)\(\)は\(\mu_\rm{B}\)\(^\ast+RT\ln{K_\rm{B}\mathit{/p_\rm{B}^\ast}}\)\(+RT\ln{x_\rm{B}}\)となります。
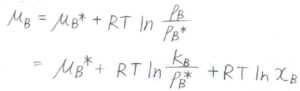
ここで、\(\mu_\rm{B}\)\(^\ast\)、\(K_\rm{B}\)\(\)、\(p_\rm{B}\)\(^\ast\)はいずれも物質に依存する定数でモル分率には依存しないので、前の2つの項を新たな標準化学ポテンシャル\(\mu^\circ\)として表すことにします。
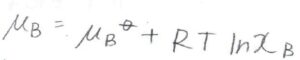
実在溶液では、モル分率を活量に置き換えるので、\(x_\rm{B}\)\(\)が\(a_\rm{B}\)\(\)になります。
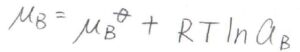
\(a_\rm{B}\)\(=p_\rm{B}\)\(/K_\rm{B}\)\(\)であり、これが\(\gamma_\rm{B}\)\(x_\rm{B}\)\(\)となります。
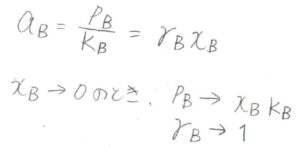
\(x_\rm{B}\)\(\)のモル分率が低いときは、どんな溶液でもヘンリーの法則が成り立つことになるので、\(x_\rm{B}\)\(\)を\(0\)に近づけていくと、\(\gamma_\rm{B}\)\(\)は\(1\)に近づいていきます。
質量モル濃度による表現
それで、モル分率から換算できる濃度を使っても活量を表すことができます。
質量モル濃度\(b\)を使うと、溶質の化学ポテンシャルは、理想溶液の化学ポテンシャルはこのように表されます。
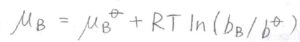
モル分率を使っていたときと異なるのは、真数の部分が濃度を標準濃度\(b^\circ\)で割った値になっていることです。
テイラー展開などで単位が合わなくなるなど、数学的におかしいことが起こるので、真数は必ず無次元量にならないといけません。
したがって、第一項の標準化学ポテンシャルも純粋なときを基準にするのではなく、標準質量モル濃度\(b^\circ\)のときの値を基準にしてとった値になります。
活量は無次元量なので、実在溶液では、真数の部分が\(a_\rm{B}\)\(\)に置き換わります。
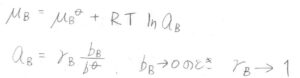
つまり、\(a_\rm{B}\)\(=\gamma_\rm{B}\)\(b_\rm{B}\)\(/b^\circ\)となります。
\(b_\rm{B}\)\(\)を\(0\)に近づけていったときには、\(\gamma_\rm{B}\)\(\)が\(1\)に近づいていくというのは変わりません。
生化学的標準状態
それで、モル分率を用いたこれまでの表し方では、その成分が純粋なときを基準にしていましたが、生化学では問題が起こります。
それは、水素イオンの化学ポテンシャルについてです。
水素イオンの活量が\(1\)の状態は、\(\rm{pH}\)\(=0\)ですから、ほとんどの生物が生存できないような過酷な環境になります。
このような状態は基準として適さないので、\(\rm{pH}\)\(=7\)の中性溶液を生化学的標準状態として採用するということをします。
\(X^{\circ \prime}\)などと表します。
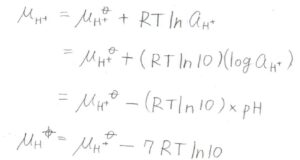
生化学で用いる標準化学ポテンシャルは純粋なときの標準量から\(7RT\ln{10}\)を引いた値になります。
活量係数のモル分率依存性
それでは最後、正則溶液について、混合エンタルピーを考えた場合と活量を考えた場合の式を照らし合わせて、活量係数のモル分率依存性を考えてみましょう。
まず、理想系の混合ギブズエネルギーの式を考えて、モル分率を活量に置き換えます。
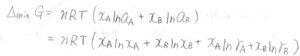
対数の前にあるモル分率は、単純に分子数を表しているだけで実在系でも変わらないので、真数だけを活量に変えます。
これを活量係数を使って表すと、\(nRT(x_\rm{A}\)\(\ln{\gamma_\rm{A}}\)\(+x_\rm{B}\)\(\ln{\gamma_\rm{B}})\)という項が現れます。
正則溶液では、これが混合エンタルピー\(n\xi RTx_\rm{A}\)\(x_\rm{B}\)\(\)に相当します。
\(\rm{A}\)\(\)と\(\rm{B}\)\(\)というラベルを入れ替えても、変化がないように考えると、\(\ln{\gamma_\rm{A}}\)\(=\xi x_\rm{B}\)\(^2\)、\(\ln{\gamma_\rm{B}}\)\(=\xi x_\rm{A}\)\(^2\)としたときに、\(n\xi RTx_\rm{A}\)\(x_\rm{B}\)\(\)という項が出てきます。
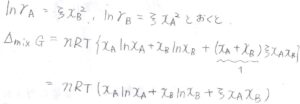
この活量係数とモル分率の関係をマルグレスの式といいます。
\(x_\rm{B}\)\(=1-x_\rm{A}\)\(\)ですから、ここから活量のモル分率依存性がわかります。
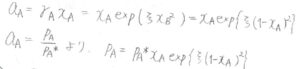
さらに、混合系における蒸気圧がモル分率によってどのように変化するのかも求めることができて、\(p_\rm{A}\)\(=p_\rm{A}\)\(^\ast x_\rm{A}\)\(\exp{[\xi (1-x_\rm{A})^2]}\)となります。
これをグラフにすると、このようになります。
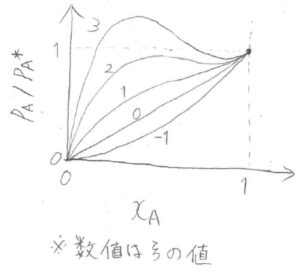
グラフ中に書かれた値は、\(\xi\)を指します。
\(x_\rm{A}\)\(\)が\(1\)に近いときには、指数の部分が\(1\)になるため、\(p_\rm{A}\)\(=x_\rm{A}\)\(p_\rm{A}\)\(^\ast\)となり、ラウールの法則が出てきます。
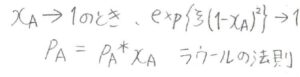
\(x_\rm{A}\)\(\)を\(0\)に近づけていくと、\((1-x_A)^2\)が\(1\)となるので、\(p_\rm{A}\)\(=p_\rm{A}\)\(^\ast x_\rm{A}\)\( \exp{(\xi)}\)となります。
\(p_\rm{A}\)\(^\ast \exp{(\xi)}\)を\(K_\rm{A}\)\(\)とすると、\(p_\rm{A}\)\(=x_\rm{A}\)\( K_\rm{A}\)\(\)となり、ヘンリーの法則が成り立つことになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
