こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(electronical spectrum of diatomic molecules 1、electronical spectrum of diatomic molecules 2)
それでは内容に入っていきます!
項記号
まず、電子遷移を表す項記号というものについて、その意味を説明していきます。
ラッセル-ソンダース項記号
始めに、二原子分子の前に、ラッセル-ソンダース項記号という原子の項記号について、説明します。
これは、小さな原子番号の原子についてのみ、適用できるものです。
電子状態を区別するのに必要なのは、次の4つの値です。
まず、それぞれの電子の軌道角運動量量子数の和を全軌道角運動量量子数\(L\)とします。
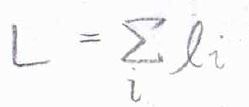
同様に、それぞれの電子のスピン量子数の和を全スピン量子数\(S\)とします。
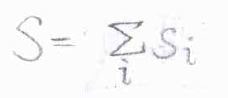
スピン多重度は、\(2S+1\)と書けます。
そして、\(L\)と\(S\)の和を全角運動量量子数\(J\)と呼びます。
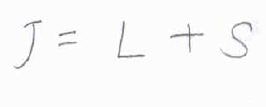
項記号の例として、励起された一重項ヘリウムと三重項ヘリウムは、それぞれ\(^1\rm{S}\)\(_0\)、\(^3\rm{S}_1\)と表現されます。
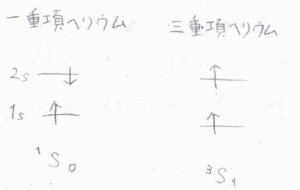
一般的に、多重度が大きいほど、エネルギーは低くなります。
これは、スピン配向の同じ電子どうしでは、交換積分が\(\displaystyle 0\)とならず、スピン配向が異なるときのエネルギーとの間に差が生じるためです。
また、基底状態にあるアルミニウムの電子配置は、\(^2\rm{P}\)\(_{3/2}\)もしくは\(^2\rm{P}\)\(_{1/2}\)になります。

記号の意味は、まず大文字のアルファベットが全軌道角運動量量子数に対応します。
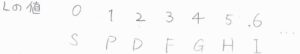
\(L=0\)は\(\rm{S}\)、\(L=1\)は\(\rm{P}\)、\(L=2\)は\(\rm{D}\)です。
これらは\(\rm{s}\)軌道、\(\rm{p}\)軌道、\(\rm{d}\)軌道など、電子の軌道角運動量量子数と軌道の対応と同じで、大文字になっただけです。
アルミニウムの例では、まず閉殻である\(\rm{Ne}\)の電子配置は無視して、軌道角運動量量子数\(l_i=0\)の\(\rm{s}\)軌道に2個と\(l_i=1\)の\(\rm{p}\)軌道に1個なので、\(L=1\)より\(\rm{P}\)となります。
そして、アルファベットの左上に書かれた数字がスピン多重度を指します。
\(\rm{s}\)軌道にある2個の電子は互いに逆のスピン配向を持っており、考慮されるのは\(\rm{p}\)軌道にある電子だけなので、全スピン角運動量\(\displaystyle S=\frac{1}{2}\)となり、多重度は\(\displaystyle 2\times \frac{1}{2}+1=2\)となります。
アルファベットの右下の数字は、全角運動量量子数\(J\)を指します。
いま2つの項記号があるのは、考えられる\(J\)の値が2つあるからです。
これらの違いは、全軌道角運動量と全スピン角運動量の相対的な配向です。
\(L=1\)の軌道角運動量と\(\displaystyle S=\frac{1}{2}\)のスピン角運動量がほぼ平行のときに\(\displaystyle J=\frac{3}{2}\)となり、反対向きのときに\(\displaystyle J=\frac{1}{2}\)となります。
スピンと軌道の磁気的な相互作用により、これらは互いに異なるエネルギーをもつことになります。
より原子番号の大きな原子になると、それぞれの電子のスピンと軌道のカップリングが強くなるため、全角運動量同士のカップリングだけでは説明できなくなっていきます。
直線型分子の項記号
次に、核電荷の小さな原子で構成された二原子分子についても、同様に考えてみます。
原子のときと異なるのは、まず球対称な形状から円筒型の形状になったということです。
そして、二原子分子では振動や回転ができます。
始めに、分子の結合軸周りの電子の全軌道角運動量量子数を\(\mathit{\Lambda}\)として、これをギリシャ文字に当てはめます。
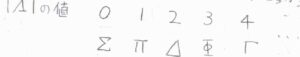
量子化された角運動量ベクトルの一方向についての成分は、\(\mathit{\Lambda} \hbar\)で与えられ、\(|\mathit{\Lambda}|=0\)の項を\(\Sigma\)、\(|\mathit{\Lambda}|=1\)の項を\(\Pi\)、\(|\mathit{\Lambda}|=2\)の項を\(\Delta\)とします。
これらの文字は、\(\rm{S}\)、\(\rm{P}\)、\(\rm{D}\)といったアルファベットの記号に対応しています。
\(\mathit{\Lambda}\)の求め方は、それぞれの電子がどの軌道にあるかを考え、それらに応じた量子数\(\mathit{\lambda}_i\)の値をすべて合算します。

\(\mathit{\lambda}_i\)は、\(\sigma\)結合について\(0\)、\(\pi\)結合について\(\pm 1\)となります。
例として、閉殻の外に\(\pi\)電子を2個もつときには、その配向によって、\(\mathit{\Lambda}=0, \pm 2\)となるため、\(\Sigma\)項、\(\Delta\)項として書かれます。
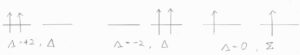
原子のときと同様に、電子のスピンと軌道の相対的な配向を\(\mathit{\Omega}\)の値で区別すると、\(|\mathit{\Omega}|\)の値が異なる準位同士ではエネルギーに差が生じることになります。

また、多重度が異なる準位同士もエネルギーが異なります。
そして、分子の項記号では、さらに選択律に重要となる2つの特徴から添え字を付けます。
パリティ
まず、反転中心をもつ分子では、パリティを考えて、ギリシャ文字の右下に書きます。
分子全体のパリティは、占有されたそれぞれの分子軌道のパリティの積となります。

そのとき、\(\rm{g}\)\(\times \rm{g}\)\(=\rm{g}\)、\(\rm{u}\)\(\times \rm{u}\)\(=\rm{g}\)、\(\rm{g}\)\(\times \rm{u}\)\(=\rm{u}\)として計算します。
付加的な対称操作
もう1つの添え字は、\(\Sigma\)項について、付加的な対称操作に対する符号の変化から付けます。
結合軸を含むある面での鏡映により符号が変化しないものには、ギリシャ文字の右上に\(+\)を書きます。
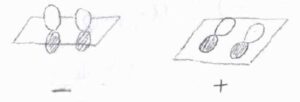
符号が反転する場合は\(-\)を書きます。
例えば、\(1\sigma_\rm{g}\)\(^1\)の電子配置であれば、\(^2\Sigma_\rm{g}\)\(^+\)となります。
選択律
これらの記号を使うと、電子スペクトルの選択律から、許容遷移と禁制遷移を判別できます。
直線型分子の電子スペクトルの選択律は、\(\mathit{\Lambda}\)の変化が\(0\)もしくは\(\pm 1\)であり、かつ全スピン量子数\(S\)が変化しない遷移が許容されるというものです。
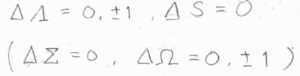
フォトンのスピンが\(1\)であることと角運動量保存則より、それぞれの電子の軌道角運動量量子数\(\mathit{\lambda}_i\)の変化は\(\pm 1\)となりますが、その結果\(\mathit{\Lambda}\)が変化するかどうかは、カップリングのしかたに依存します。
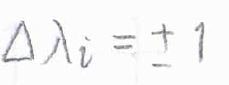
また、全スピン量子数\(S\)の変化が\(0\)というのは、フォトンのスピンが電子のスピンに影響しないことからきたものです。
対称性についての選択律は、次のようになります。
結合軸を含む鏡映面についての選択律
まず、\(\Sigma\)項から\(\Sigma\)項への遷移では、右上の添え字として書いた符号が変化しない遷移だけが許容されます。
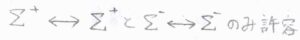
例えば、結合軸が\(z\)軸と平行な直線型分子について、遷移双極子モーメントを考えます。
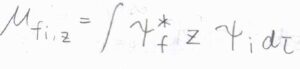
\(x\)と\(y\)は\(\Pi\)対称性をもち、遷移双極子モーメントの成分が\(0\)となるため、\(z\)成分だけ考えれば判別できます。
\(z\)は鏡映により符号が変化しないので\(+\)であり、それらの積を考えると、遷移の前後で符号が変化しない場合に、被積分関数も\(+\)の対称性をもちます。
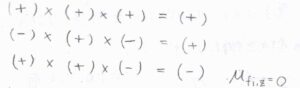
遷移の前後で符号が変化する場合は、被積分関数も\(-\)の対称性をもつということになり、積分は\(0\)になります。
したがって、鏡映についての対称性が変化する遷移は、禁制遷移です。
ラポルテの選択律
そして、反転中心をもつ分子についてのパリティは、\(\rm{u}\)\(\leftarrow \rm{g}\)、\(\rm{g}\)\(\leftarrow \rm{u}\)というように遷移の前後で変化するものが許容されます。
この法則は、ラポルテの選択律と言います。
これは、\(x\)、\(y\)、\(z\)がすべて中心に対して反対称であることから、導くことができます。
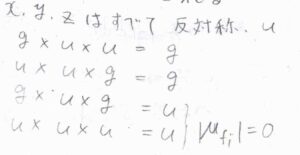
禁制遷移が起こる要因
次に、この選択律に反して禁制遷移が起こることがあるので、その要因についてもお話しします。
振電遷移
まず、分子の非対称的な振動により対称中心が失われると、パリティの分類がなくなることで、本来禁制だった遷移がわずかに許容されることがあります。
例えば、すべての\(\rm{d}\)軌道が\(\rm{g}\)であることから、本来\(\rm{d}\)\(-\rm{d}\)遷移は禁制となりますが、分子の非対称的な振動によって許容されます。

遷移強度が分子の振動から導かれる遷移のことは、振電遷移と言います。
多光子過程
また、レーザー光のようにフォトンの数密度が大きい入射光を当てたときには、1つの分子に2個以上のフォトンが吸収されることがあります。
これを多光子過程と言います。
例として、2個の電子を吸収する過程では、全体として\(\rm{g}\)\(\leftarrow \rm{g}\)、\(\rm{u}\)\(\leftarrow \rm{u}\)の遷移が許容されるため、単一フォトン分光法では観測できない状態について調べることができます。
スピン-軌道カップリング
そのほかに、これら全角運動量だけを使った考え方は、軌道とスピンのカップリングが比較的小さな分子にしか適用できないため、核電荷の大きな原子で構成された分子では、禁制遷移だったものが許容されることが考えられます。
振動構造
ここで、実際の電子スペクトルの例を示します。
こちらは、二原子分子ではありませんが、\(25^\circ \rm{C}\)の\(\rm{SO}_2\)気体に紫外線を照射して得られる、横軸を入射光の波長、縦軸をモル吸光係数としたスペクトルです。
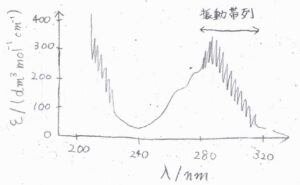
特徴として、吸収ピークが並んで現れる振動構造が見られます。
これは、電子遷移と同時に振動遷移も起こったことを示唆しています。
フランク-コンドンの原理
電子遷移と同時に振動遷移が起こる機構を理解するためには、フランク-コンドンの原理が用いられます。
フランク-コンドンの原理は、電子は原子核よりもはるかに大きな質量をもっているため、変化に対する応答にかかる時間に大きな差が生じるとするものです。
古典力学的な説明
電子遷移と振動遷移の機構を古典的にイメージすると、次のようになります。
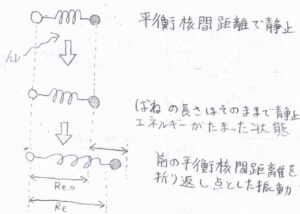
まず、振動しておらず静止していた分子が紫外線や可視光を吸収します。
しかし、原子核はその場にほぼ静止したままなので、エネルギーは化学結合に蓄積されることになります。
これは、横軸に核間距離をとったポテンシャル図では、真上に点が移動することになるため、垂直遷移と表現されます。
そして、ばねにひずみがかかったことで、分子は振動を開始することになります。
その際、静止していたときの平衡核間距離は、振動の折り返しで原子核が静止したときの核間距離と一致します。
量子力学的な説明
量子力学的な説明では、原子核が静止しているとする代わりに、始めの力学的な状態を維持しようとすると考えます。
つまり、電子遷移によって波動関数がほとんど変化しないということになります。
遷移の機構をポテンシャル図に書くと、このようなイメージです。

まず、基底電子状態のとある振動状態に分子があるとします。
その波動関数は\(\psi_\rm{i}\)です。
ここから電磁波を吸収して励起電子状態に遷移します。
その振動状態の波動関数\(\psi_\rm{f}\)が、遷移前の波動関数\(\psi_\rm{i}\)のピークとほぼ同じ核間距離で主要なピークをもてば、高い確率で遷移が起こるということになります。
一般的に、電子状態が励起されると、反結合性の差から平衡核間距離は大きくなるので、グラフでいうと波動関数の左側でポテンシャルカーブに差し掛かった部分が重要になることが多いです。
そして、振動量子数\(v=0\)のときを除けば、波動関数のピークはポテンシャルカーブ近傍にあるので、複数の振動準位へ遷移が起こりうるということになります。
フランク-コンドン因子
遷移強度は、次のように考えることができます。
まず、状態\(\rm{i}\)から\(\rm{f}\)への遷移について、遷移双極子モーメントを\(\boldsymbol{\mu}_\rm{fi}\)、電気双極子モーメント演算子を\(\hat{\boldsymbol{\mu}}\)とします。
\(\hat{\boldsymbol{\mu}}\)は、すべての電子と原子核を考慮して、このように書きます。
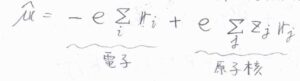
\(Z_j\)は原子核にある陽子の個数です。
ボルン-オッペンハイマー近似の範囲で、これを遷移双極子モーメントの式に当てはめると、このようになります。
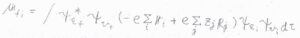
さらに、電子と原子核の因子に分解すると、下のように書けます。
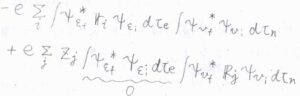
第二項については、異なる2つの電子状態が直交することより\(0\)となります。
この遷移双極子モーメントのうち、純粋な電子遷移の遷移双極子モーメントを\(\boldsymbol{\mu}_{\mathit{\varepsilon}, \rm{fi}}\)、振動状態の重なり積分を\(S(v_\rm{i}, \mathit{v}_\rm{f})\)とします。
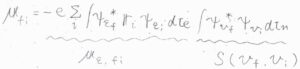
すると、遷移強度は遷移双極子モーメントの大きさの\(2\)乗に比例することから、重なり積分\([S(v_\rm{i}, \mathit{v}_\rm{f})]^2\)に比例することになります。
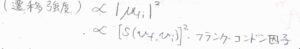
\([S(v_\rm{i}, \mathit{v}_\rm{f})]^2\)のことは、フランク-コンドン因子と言います。
回転構造
続いて、分子の回転が電子スペクトルに及ぼす影響について考えていきます。
結合長への影響は振動遷移よりも電子遷移の方がはるかに大きいため、慣性モーメント、ひいては回転定数に大きな変化が生じます。
基底電子状態と励起電子状態における回転定数をそれぞれ\(\tilde{B}\)、\(\tilde{B’}\)、吸収波数のうち振動遷移由来の成分を\(\tilde{\nu}\)とすると、まず\(\Delta J=-1\)のP枝の吸収波数は、\(\tilde{\nu}-(\tilde{B’}+\tilde{B})J+(\tilde{B’}-\tilde{B})J^2\)となります。
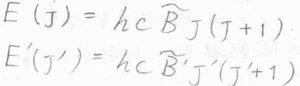
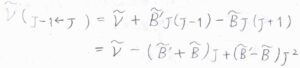
同様に、Q枝、R枝についても吸収波数を求めると、こちらのようになります。
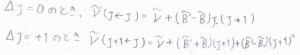
電子状態の励起により、平衡核間距離が大きくなって、回転定数が小さくなると、\(\Delta J=+1\)のR枝の間隔は、だんだん狭くなっていきます。
そして、\((\tilde{B}-\tilde{B’})(J+1)\gt \tilde{B’}+\tilde{B}\)となった\(J\)からは、\(J\)の増加にともなって吸収波数が減少していくことになります。
反対に、\(\tilde{B}\)が\(\tilde{B’}\)より小さいときには、P枝が収束していきます。
そして、\((\tilde{B’}-\tilde{B})J\gt \tilde{B’}+\tilde{B}\)となった\(J\)からは、吸収波数が増大していきます。
電子スペクトルでは振動由来のピークが並ぶため、回転構造をはっきりと見ることは困難ですが、仮に1つの振動遷移だけを取り出せたとすると、こちらの図のようになります。
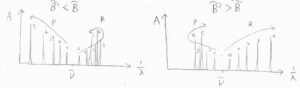
左が\(\tilde{B} \gt \tilde{B’}\)のとき、右が\(\tilde{B} \lt \tilde{B’}\)のときです。
それぞれR枝、P枝があるところから引き返してくる並び方をします。
ちょうど引き返した部分のことは、帯頭と呼ばれます。
練習問題
最後に、練習問題をやって終わろうと思います。
(1) 酸素分子の電子スペクトルにおいて、振動や多光子過程を考えない場合、これら3つの遷移が許容されるかどうかを判定してみてください。

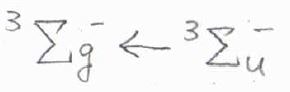

(2) 電子遷移により平衡核間距離が\(R_\rm{e}\)から\(R’_\rm{e}\)になったとします。
振動状態が互いの基底状態であったとき、重なり積分\(S(0, 0)\)はどのように表されるでしょうか?
ただし、ポテンシャルの非調和性を無視できるとして、基底状態の波動関数は、こちらの式で与えられるものとします。
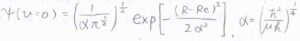
\(R\)は核間距離です。

表の中で波線を引いた部分が選択律に反するもので、禁制遷移となります。
表より答えは、2つ目だけが許容遷移で、1つ目と3つ目が禁制遷移となります。
(2)遷移前と遷移後の波動関数をそれぞれ\(\psi_0\)、\(\psi_0’\)とします。
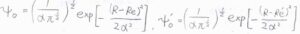
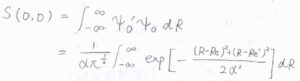
途中、\(\displaystyle \alpha z=R-\frac{R_\rm{e}+\mathit{R’}_\rm{e}}{2}\)として変形すると、ガウス積分の公式より、最終的に\(\displaystyle S(0, 0)=\exp{[-\frac{(R_\rm{e}-\mathit{R’}_\rm{e})^2}{4\alpha^2}]}\)となります。
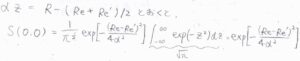
ちなみに、フランク-コンドン因子は、これの\(2\)乗なので、\(\displaystyle \exp{[-\frac{(R_\rm{e}-\mathit{R}_\rm{e}’)^2}{2\mathit{\alpha}^2}]}\)と書けます。
平衡核間距離が等しいときに\(1\)となり、差が大きくなっていくにつれて、\(0\)まで減衰していきます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!