こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(transition state theory)
それでは内容に入っていきます!
遷移状態理論
まず、今回想定している系は、次のようなものです。
理想気体である\(\rm{A}\)と\(\rm{B}\)が1分子ずつ反応して、理想気体の生成物\(\rm{P}\)が1分子生成します。
ポテンシャル図は、こちらのとおりです。
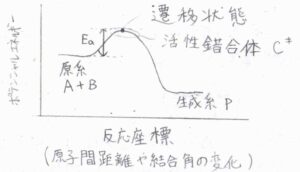
横軸は反応座標とされていますが、これは原子間距離や結合角の変化の度合いを表すものです。
遷移状態とは、ポテンシャルエネルギーが最も高くなる決定的な配置を意味し、ポテンシャル図では点として表現されます。
その遷移状態前後のごく限られた領域に対応する原子の集団のことは、活性錯合体と呼ばれます。
ここでは、\(\rm{C}\)\(^\ddagger\)と表すことにします。
本記事のテーマである遷移状態理論は、活性錯合体理論とも呼ばれており、反応物である\(\rm{A+B}\)と活性錯合体\(\rm{C}\)\(^\ddagger\)との前駆平衡を考えることで、反応速度定数の定式化を行います。
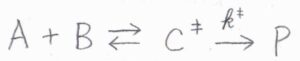
前駆平衡については、こちらを参照してください。

\(\rm{A}\)\(+\rm{B}\)と\(\rm{C}\)\(^\ddagger\)との平衡定数を\(K^\ddagger\)、\(\rm{C}\)\(^\ddagger\)から\(\rm{P}\)が生成する素反応の速度定数を\(k^\ddagger\)と表すことにします。
平衡を考えるため、\(\rm{P}\)の生成速度は\(\rm{C}\)\(^\ddagger\)の分解速度よりも十分遅いものとします。
それぞれの化学種の分圧を\(p\)、標準圧力を\(p^\circ\)とすると、\(\displaystyle K^\ddagger=\frac{p_\rm{C^\ddagger}\mathit{p}^\circ}{p_\rm{A}\mathit{p}_B}\)と書けます。
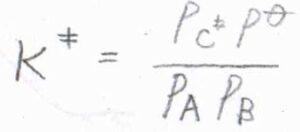
さらに、理想気体の状態方程式より、化学種\(\rm{J}\)について\(p_\rm{J}\)\(=RT[\rm{J}]\)と書けるため、\(\displaystyle K^\ddagger=\frac{p^\circ[\rm{C}^\ddagger]}{RT[\rm{A}][B]}\)と変形できます。
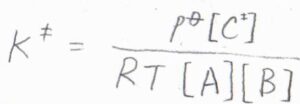
ここで\([\rm{J}]\)は、平衡状態における化学種\(\rm{J}\)のモル濃度です。
これを\([\rm{C}\)\(^\ddagger]\)について整理すると、\([\rm{C}\)\(\displaystyle ^\ddagger]=\frac{RT}{p^\circ}K^\ddagger[\rm{A}\)\(][\rm{B}]\)となります。
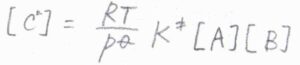
\(\rm{P}\)の生成速度\(v\)は、\(k^\ddagger[\rm{C}\)\(^\ddagger]\)で与えられることから、全体の反応は二次反応になることがわかります。
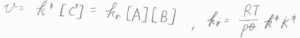
その反応速度定数\(k_\rm{r}\)は、\(\displaystyle \frac{RT}{p^\circ}k^\ddagger K^\ddagger\)と書けます。
ここからは、\(k^\ddagger\)と\(K^\ddagger\)を個別に定式化することで、\(k_\rm{r}\)を求めていきます。
\(k^\ddagger\)について
まず、反応物系の2つの分子が活性錯合体を作れるほど接近すると、比較的弱い結合が形成され、分子間距離は短くなります。

一方で、この新たな結合が長くなれば、結合の開裂が起こると考えられます。
このようにして、活性錯合体は反応座標に沿った振動運動をします。
これを一次元調和振動子とみなして、その振動数を\(\nu^\ddagger\)とすれば、活性錯合体が遷移状態を通過して、生成物\(P\)まで反応座標が進む頻度も\(\nu^\ddagger\)で与えられることになります。
このことから、速度定数\(k^\ddagger=\nu^\ddagger\)と書けます。
ただし厳密には、反応座標に沿った振動運動以外の影響、たとえば回転による遠心力の寄与などが重要になることがあるので、\(k^\ddagger\)は\(\nu^\ddagger\)に比例すると考えます。

比例定数である\(\kappa\)は、透過係数と呼ばれます。
しかし計算上は、ほぼ\(1\)として扱われることが多いです。
\(K^\ddagger\)について
次に、\(K^\ddagger\)について考えていきます。
ここでは、前回の物理化学の動画で導出した、平衡定数とモル分配関数の関係を使います。
すると、\(\displaystyle K^\ddagger=\frac{N_\rm{A}\mathit{q}_{C^\ddagger}^\circ}{q_\rm{A}^\circ \mathit{q}_B^\circ}\exp{(-\frac{\Delta_\rm{r}\mathit{E}_0}{\mathit{RT}})}\)と書けます。
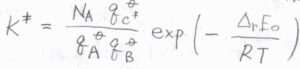
ここで、\(N_\rm{A}\)はアボガドロ数、\(q\)はモル分配関数、\(\Delta_\rm{r}\)\(E_0\)は反応による零点エネルギーの変化量です。
詳しくは、こちらを参照してください。

さらに、\(q_\rm{C^\ddagger}\)\(^\circ\)の変形を考えます。
まず、反応座標に沿った振動運動のモードについての振動分配関数\(q_\rm{C^\ddagger}\)\(^\rm{V}\)は、先ほど導入した振動数\(\nu^\ddagger\)を使って、\(\displaystyle \frac{1}{[1-\exp{(-h\nu^\ddagger/k_\rm{B}\mathit{T})}]}\)と書けます。
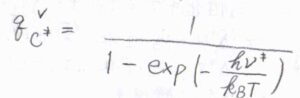
ここで、\(h\)はプランク定数、\(k_\rm{B}\)はボルツマン定数です。
詳しくは、こちらを参照してください。

活性錯合体の反応座標に沿った振動は、開裂も起こりうるものなので、一般的な分子振動の振動数に比べると、とても小さいと考えられます。
そのため、室温でも振動特性温度より十分に高いとして近似をすれば、\(q_\rm{C^\ddagger}\)\(^\rm{V}\)\(\displaystyle \approx \frac{k_\rm{B}\mathit{T}}{h\nu^\ddagger}\)と考えることができます。
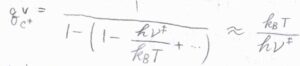
活性錯合体のほかの分子運動についてのモル分配関数を\(\bar{q_\rm{C^\ddagger}}\)とすれば、\(q_\rm{C^\ddagger}\)\(\displaystyle ^\circ=\frac{k_\rm{B}\mathit{T}}{h\nu^\ddagger}\bar{q_\rm{C^\ddagger}}\)と書くことができます。
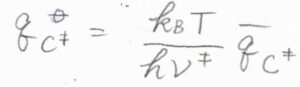
ここで考えていることをポテンシャル図にすると、こちらのようなイメージです。
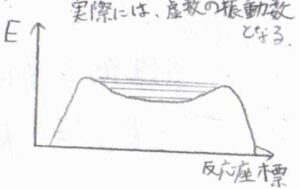
遷移状態の近傍で、ポテンシャルに広く浅いくぼみができていて、錯合体はほぼ古典的な調和振動をします。
ただ、この図はあくまでイメージに過ぎず、実際にエネルギー障壁の頂点付近にくぼみが観測されることはほとんどありません。
ポテンシャルが上に凸のとき、形式的な力の定数は負の値であり、振動数は虚数になります。
この振動数が虚数である問題は、このまま読み進めていくとわかりますが、最終的に導かれる反応速度定数に影響しません。
そのため、虚数の振動数をそのまま使うことにして、話を進めます。
アイリングの式
平衡定数\(K^\ddagger\)の式に\(q_\rm{C^\ddagger}\)\(\displaystyle ^\circ=\frac{\bar{q_\rm{C^\ddagger}}k_\rm{B}\mathit{T}}{h\nu^\ddagger}\)を代入すると、\(\displaystyle K^\ddagger=\frac{k_\rm{B}\mathit{T}}{h\nu^\ddagger}\bar{K^\ddagger}\)と書けます。
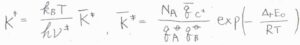
ここで\(\bar{K^\ddagger}\)は、反応座標に沿った振動のモードを除いて計算される平衡定数であり、\(\displaystyle \frac{N_\rm{A}\bar{q_\rm{C^\ddagger}}}{q_\rm{A}^\circ \mathit{q}_B^\circ}\exp{(-\frac{\Delta_\rm{r}\mathit{E}_0}{\mathit{RT}})}\)と表されます。
最後に、反応速度定数\(k_\rm{r}\)の式に以上の結果を代入すると、\(k_\rm{r}\)\(\displaystyle =\kappa\frac{k_\rm{B}\mathit{T}}{h}\frac{RT}{p^\circ}\bar{K^\ddagger}\)という関係が得られます。
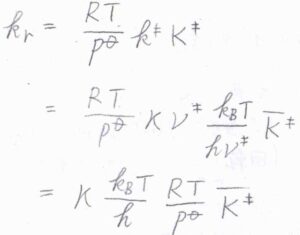
虚数の振動数である\(\nu^\ddagger\)は約分で消えるので、反応速度定数は実数として得られます。
\(\displaystyle \frac{RT}{p^\circ}\)は、標準圧力における理想気体のモル体積ですが、これを平衡定数に組み込んだものを\(\bar{K_\rm{C^\ddagger}}\)とおけば、\(k_\rm{r}\)\(\displaystyle =\kappa\frac{k_\rm{B}\mathit{T}}{h}\bar{K_\rm{C^\ddagger}}\)となります。


この式は、アイリングの式と呼ばれており、反応系の分子と活性錯合体の分子パラメータおよび透過係数\(\kappa\)から、反応速度定数が計算できることを示しています。
ただし、活性錯合錯合体の大きさや形がわからない以上、分光法などによって分配関数を計算することは非常に困難です。
熱力学的な見方
そこで、反応系の分子と活性錯合体が平衡状態にある考え方は残しつつ、熱力学量によって活性化の過程を表す方法が考えられました。
ここからは、遷移状態理論から得られる結果を、アレニウスの式や衝突理論と比べていきます。
ただ、先ほど出てきた平衡定数\(K^\ddagger\)は虚数なので、熱力学量を実数として求められません。
ここでは、振動モードを1つ除いた平衡定数\(\bar{K^\ddagger}\)から遷移状態の熱力学量が実数として求められると仮定した結果を示します。
反応系から遷移状態に至るまでの標準ギブズエネルギー変化を、活性化ギブズエネルギー\(\Delta^\ddagger G\)とすると、それが\(-RT\ln{\bar{K^\ddagger}}\)と表されます。
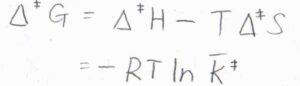
こちらも参照してください。

また、活性化エンタルピー\(\Delta^\ddagger H\)と活性化エントロピー\(\Delta^\ddagger S\)を使うと、温度一定として\(\Delta^\ddagger G=\Delta^\ddagger H-T\Delta^\ddagger S\)であるため、反応速度定数\(k_\rm{r}\)は、\(\displaystyle \kappa \frac{k_\rm{B}\mathit{T}}{h}\frac{RT}{p^\circ}\exp{(-\frac{\Delta^\ddagger H}{RT}+\frac{\Delta^\ddagger S}{R})}\)と書けます。
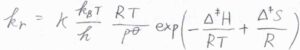
もし、活性化エンタルピーと活性化エントロピーの温度依存性が無視できるならば、縦軸に\(\displaystyle \ln{(\frac{k_\rm{r}}{\mathit{T}^2})}\)、横軸に\(\displaystyle \frac{1}{T}\)をとったときに、こちらの図のような直線が書けることになります。
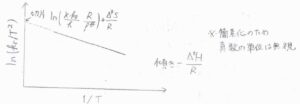
\(\kappa=1\)と仮定すれば、活性化エンタルピーと活性化エントロピーを実験的に求めることができます。
そして、アレニウスパラメータである活性化エネルギー\(E_\rm{a}\)の形式的な定義\(\displaystyle RT^2(\frac{\partial \ln{k}}{\partial T})\)に\(k_\rm{r}\)の式を代入すれば、\(E_\rm{a}\)\(=\Delta^\ddagger H+2RT\)となります。
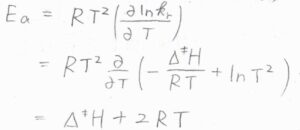
(これはあくまで、気相中における反応に限った結果であり、液相中では\(k_\rm{r}\)の式に\(\displaystyle \frac{RT}{p^\circ}\)がないため、\(E_\rm{a}\)\(=\Delta^\ddagger H+RT\)となります。)
\(E_\rm{a}\)\(=\Delta^\ddagger H+2RT\)という関係を利用して、\(k_\rm{r}\)の式から\(\Delta^\ddagger H\)を消去すると、もう1つのアレニウスパラメータである頻度因子\(A\)が、\(\kappa \rm{e}\)\(\displaystyle ^2\frac{k_\rm{B}\mathit{T}}{h}\frac{RT}{p^\circ}\exp{(\frac{\Delta^\ddagger S}{R})}\)と書けることがわかります。
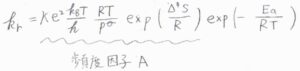
アレニウスの式については、こちらを参照してください。

もしも分子\(\rm{A}\)と\(\rm{B}\)の単純な出会いによって錯合体ができるならば、衝突理論から予想される頻度因子と一致するはずです。
衝突理論については、こちらを参照してください。

錯合体が形成されれば分子数が減少するため、そもそも活性化エントロピー\(\Delta^\ddagger S\)は負となりますが、実際のエントロピー変化は、衝突理論から予想される活性化エントロピーよりもさらに小さくなることがあります。
これは、結合を形成するために、衝突するべき正しい方向など立体的な条件に対応しています。
その余分なエントロピー減少分を\(\Delta^\ddagger S_\rm{steric}\)とすると、立体因子\(P\)は、\(\displaystyle \exp{(\frac{\Delta^\ddagger S_\rm{steric}}{\mathit{R}})}\)と書けます。
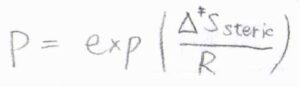
衝突理論では、現実に照らし合わせるために最後に組み込んだ立体因子ですが、遷移状態理論では、始めからエントロピーに組み込まれています。
直線自由エネルギー関係(LFER)
活性化ギブズエネルギーや活性化エンタルピー、活性化エントロピーの値は、特に溶液中の有機反応について、反応速度の実験結果を記載する際によく用いられています。
これには、反応速度定数と平衡定数の間に成り立つことが多い、ある経験則が関係しています。
一般的に、遷移状態のギブズエネルギーに依存する反応速度定数と、生成系のギブズエネルギーに依存する平衡定数はまったく異なる概念ですが、その間に比例関係が認められることがよくあります。
それは、平衡定数の対数に対して、反応速度定数の対数をプロットすることで確かめることができて、この関係のことを直線自由エネルギー関係、略してLFERと言います。
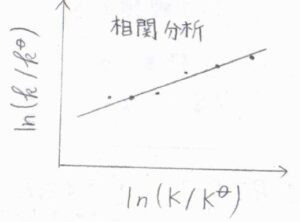
この関係が成り立つ反応同士では、標準反応ギブズエネルギーが大きいほど、活性化ギブズエネルギーも大きくなります。
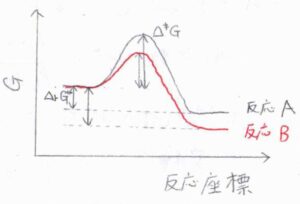
つまり、熱力学的に起こりやすい反応ほど、速く進行するということです。
逆に、この関係が認められない場合、反応物の構造の違いにより反応機構に変化が生じていることが疑われます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




