こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(collision theory)
それでは内容に入っていきます!
アレニウスの式
まず、改めてアレニウスの式を確認しておきます。
多くの反応で、反応速度定数\(k\)は、\(\displaystyle A\exp{(-\frac{E_\rm{a}}{\mathit{RT}})}\)という式で書けることが実験的に求められました。
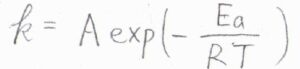
\(R\)が気体定数、\(T\)が絶対温度です。
\(A\)と\(E_\rm{a}\)は、実験的に決定される定数で、アレニウスパラメータと言います。
また、それぞれは頻度因子、活性化エネルギーと呼ばれます。
指数の部分がボルツマン分布に由来しているということはお話ししましたが、頻度因子が何を反映したものかについては、まだ話していません。
詳しくは、こちらも参照してください。

衝突頻度から導かれる予想
今回は、\(\rm{A}\)と\(\rm{B}\)が\(\rm{P}\)へと変化するという2次素反応を例に考えることにします。
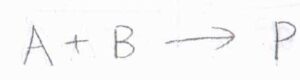
2つの分子が反応をするためには、互いに電子のやり取りができるくらい接近する必要があります。
そこから、反応速度は衝突頻度に比例するはずであると予想します。
衝突頻度を左右する要因としては、まず分子の大きさがあります。

大きな分子であるほど、衝突が起こりやすくなります。
2分子が接触した瞬間について考えると、その中心間距離は、それぞれの分子を球に見立てたときの半径の和になります。
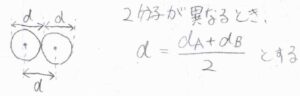
2つの分子の直径が等しいとき、中心間距離は分子の直径です。
そこで、中心間距離の最小値を\(d\)と表すことにします。
本来、分子の衝突は多体問題となりますが、ここで、ある1つの\(\rm{A}\)の分子の並進運動のみに着目します。
他の分子はすべて静止しているとして、単体問題にします。
分子1つの衝突頻度、すなわち単位時間あたりの衝突回数は、こちらの図で示した円柱の中にある分子中心の個数になります。
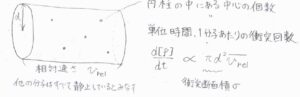
まず、底面の面積は、\(\pi d^2\)です。
これを衝突断面積と呼び、\(\sigma\)と表すことにします。
高さは、分子が単位時間あたりに進む距離で、他の分子の並進運動の速さを\(0\)とした、相対的な速さになります。
ここでは、\(v_\rm{rel}\)と表すことにします。
反応速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は、衝突断面積\(\sigma\)と相対速さの平均値\(\bar{v_\rm{rel}}\)に比例します。
こうなると、分子の大きさ以外にも反応速度に影響を及ぼすパラメータがあることがわかります。
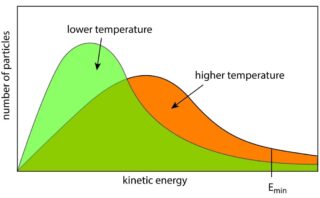
分子がボルツマン分布に従っているとき、速さの分布は、こちらのマクスウェル-ボルツマン分布で書けます。
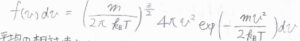
ここで、\(k_\rm{B}\)はボルツマン定数、\(m\)は分子1個の質量です。
詳しくは、こちらを参照してください。
相対速さ\(v_\rm{rel}\)の平均を求めるには、質量\(m\)を換算質量\(\mu\)と書き換えて、速さ\(v\)の期待値を計算します。
換算質量\(\displaystyle \mu=\frac{m_\rm{A}\mathit{m}_\rm{B}}{m_\rm{A}+\mathit{m}_\rm{B}}\)で与えられ、2分子が同じ質量のときは、\(\displaystyle \frac{m}{2}\)となります。
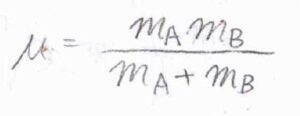
詳しくは、こちらを参照してください。

ガウス積分の公式も使って計算すると、期待値は\(\displaystyle \sqrt{\frac{8k_\rm{B}\mathit{T}}{\pi \mu}}\)となります。
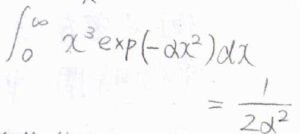
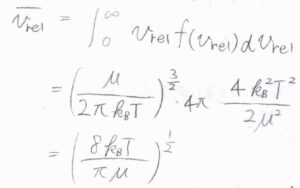
したがって、反応速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{[\rm{d}\mathit{t}}\)は\(\sqrt{T}\)に比例し、\(\sqrt{\mu}\)には反比例することになります。
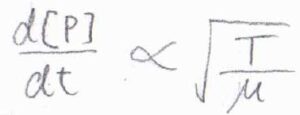
そして、先ほどの円柱の中にある分子中心の個数は、分子の数密度からわかります。
数密度を\(\rho\)と表すことにすると、反応速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は、\(\rho_\rm{B}\)に比例することになります。
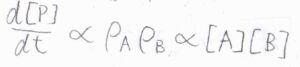
\(\rm{B}\)の分子の単体問題とすれば、\(\rho_\rm{A}\)に比例することになるので、どちらにも比例することになります。
数密度をアボガドロ数\(N_\rm{A}\)で割ればモル濃度になるので、反応速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は\([\rm{A}\)\(][\rm{B}]\)に比例することになります。
単位時間、単位体積あたりの衝突回数のことは、衝突密度と言います。
ここでは、\(z_\rm{AB}\)と表します。
定義より、\(z_\rm{AB}\)は\(\sigma \bar{v_\rm{rel}}\)\(\rho_\rm{A}\)\( \rho_\rm{B}\)で与えられ、\(\pi d^2 N_\rm{A}\)\(\displaystyle ^2 \sqrt{\frac{8\pi k_\rm{B} \mathit{T}}{\pi \mu}}[\rm{A}\)\(][\rm{B}]\)とも書けます。

2分子が同種であるときには、\(\displaystyle \mu=\frac{m_\rm{A}}{2}\)より、\(\bar{v_\rm{rel}}\)は絶対的な速さの平均値\(\bar{v}\)の\(\sqrt{2}\)倍となります。

\(z_\rm{AA}\)は、\(\displaystyle \frac{1}{2}\pi d^2 N_\rm{A}\)\(\displaystyle ^2 \sqrt{\frac{16\pi k_\rm{B} \mathit{T}}{\pi \mu}}[\rm{A}\)\(]^2\)となります。

ダブルカウントを回避するために、\(2\)で割る必要があります。
ただし、衝突が起こったからといって、必ずしも反応が起こるとは限りません。
分子がボルツマン分布に従っている場合、反応可能な運動エネルギーの最小値を\(E’\)として、これよりも高いエネルギーの状態にある確率に反応速度は比例するはずです。
したがって、反応速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は\(\displaystyle \exp{(-\frac{E’}{RT})}\)に比例します。
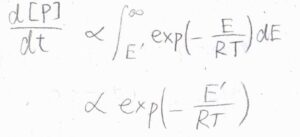
以上のことより、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は、\(\displaystyle \sigma \sqrt{\frac{T}{\mu}}\exp{(-\frac{E’}{RT})}[\rm{A}\)\(][\rm{B}]\)に比例します。
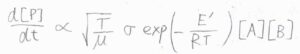
反応速度定数\(k\)は、これを\([\rm{A}\)\(][\rm{B}]\)で割った値であるため、\(\displaystyle \sigma \sqrt{\frac{T}{\mu}} \exp{(-\frac{E’}{RT})}\)に比例することになります。
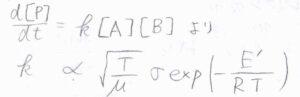
衝突のしかたの違いから導かれる予想
単位時間あたりに\(1\)つの分子が反応できる回数は、単純な衝突頻度よりも小さくなると考えられます。
それは、分子のもつ運動エネルギーには分布があり、反応に必要なエネルギーをもっていない場合は、衝突しても反応が起こらないからというのが、ここまでの考え方でした。
ここでは、少し違うイメージでエネルギーの分布を考慮してみます。
反応の頻度を、こちらの図の中で赤で示した円柱の内側にある分子中心の個数と考えます。
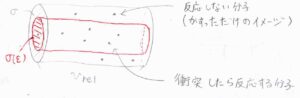
中心がこの円柱の外側にあって、黒で示した円柱の内側にある分子とは反応せず、衝突だけが起こります。
正面から衝突しないと反応は起こらず、ただ表面がかすっただけでは反応は起こらないイメージです。
運動エネルギー\(\varepsilon\)が大きくなれば、当たり方が弱くても反応が起こるようになると考えられるので、この赤い円柱の断面積は、単調増加する\(\varepsilon\)の関数になります。
これを\(\sigma (\varepsilon)\)と表すことにします。
\(\sigma (\varepsilon)\)の半径を\(a\)として、ちょうど反応が起こるか起こらないかの境界で2分子が接触したときの位置関係を表した図がこちらです。
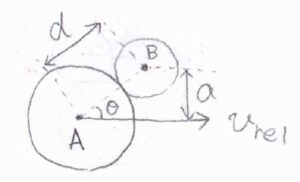
2つの分子の中心を点\(\rm{A}\)、点\(\rm{B}\)として、速度ベクトル\(\displaystyle \boldsymbol{v}_\rm{rel}\)とベクトル\(\boldsymbol{\rm{AB}}\)がなす角を\(\theta\)とします。
\(\displaystyle \cos{\theta}=\sqrt{\frac{d^2-a^2}{d^2}}\)であるため、\(\displaystyle \cos{\theta}=\sqrt{\frac{\sigma-\sigma(\varepsilon)}{\sigma}}\)となります。

反応に関与するのは、\(\boldsymbol{\rm{AB}}\)方向への運動エネルギーだけだと考えると、実効の速さは\(v_\rm{rel}\)\( \cos{\theta}\)となり、実効の運動エネルギーは\(\varepsilon \cos^2{\theta}\)となります。

反応に必要な最小値を\(\varepsilon_\rm{a}\)とすると、\(\varepsilon_\rm{a}\)\(\displaystyle =\varepsilon\frac{\sigma-\sigma(\varepsilon)}{\sigma}\)と書けます。
これを整理すると、\(\displaystyle \sigma(\varepsilon)=\sigma(1-\frac{\varepsilon_\rm{a}}{\varepsilon})\)という関係が導かれます。
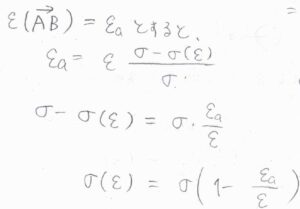
横軸を\(\varepsilon\)、縦軸を\(\sigma(\varepsilon)\)としてグラフを書くと、反比例の平行移動なので、こちらのようになります。
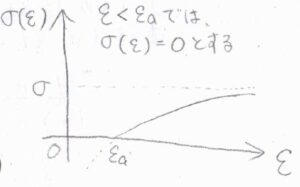
\(\varepsilon\)が大きいときには、\(\sigma(\varepsilon)\)は\(\sigma\)とほぼ等しくなります。
\(\varepsilon\)が\(\varepsilon_\rm{a}\)よりも小さいときには、\(\sigma(\varepsilon)\)が負の値となりますが、面積は\(0\)以上になるはずなので、この範囲では\(\sigma(\varepsilon)=0\)と考えます。
\(\sigma(\varepsilon)=0\)は、たとえ真正面から衝突しても反応が起こらないという意味になります。
\(\sigma(\varepsilon)\)と反応速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)の関係は、次のように考えます。
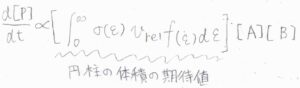
運動エネルギー\(\varepsilon\)には分布があるので、先ほどの赤で示した円柱の体積の期待値をとります。
それが\(\displaystyle \int_0^\infty \sigma(\varepsilon)v_\rm{rel}\)\( f(\varepsilon)\rm{d}\)\(\varepsilon\)です。
この体積の平均値に数密度をかけたものが、\(1\)分子あたりの反応頻度の平均値になります。
したがって\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は、平均の体積と\([\rm{A}\)\(][\rm{B}]\)に比例します。
\(f(\varepsilon)\rm{d}\)\(\varepsilon\)は、マクスウェル-ボルツマン分布の変数を速さから運動エネルギーに書き換えたものです。
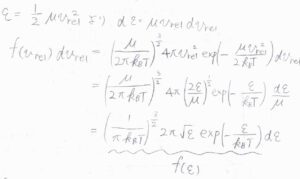
丁寧に変形していけば、\(\displaystyle f(\varepsilon)=(\frac{1}{\pi k_\rm{B}\mathit{T}})^\frac{3}{2}2\pi \sqrt{\varepsilon}\exp{(-\frac{\varepsilon}{k_\rm{B} \mathit{T}})}\)となります。
期待値の積分で定数部分を前に出すと、結局\(\displaystyle \int_{\varepsilon_\rm{a}}^{\infty}\)\( (\varepsilon-\varepsilon_\rm{a}\)\(\displaystyle )\exp{(-\frac{\varepsilon}{k_\rm{B} \mathit{T}})}\rm{d}\)\(\varepsilon\)の計算をすればよいことになります。
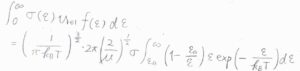
\(\displaystyle \int_{\varepsilon_\rm{a}}^{\infty}\)\(\displaystyle \varepsilon\exp{(-\frac{\varepsilon}{k_\rm{B} \mathit{T}})}\rm{d}\)\(\varepsilon\)を部分積分の公式を使って変形すると、第一項が\(\displaystyle \int_{\varepsilon_\rm{a}}^{\infty}\)\( \varepsilon_\rm{a}\)\(\displaystyle \exp{(-\frac{\varepsilon}{k_\rm{B} \mathit{T}})}\rm{d}\)\(\varepsilon\)と等しくなるので、上の積分の答えは、第二項の\(k_\rm{B}\)\(\displaystyle ^2 T^2\exp{(-\frac{\varepsilon_\rm{a}}{k_\rm{B}\mathit{T}})}\)となります。
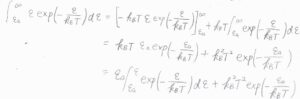
\(\varepsilon_\rm{a}\)をモルあたりの量にしたものを\(E_\rm{a}\)とすると、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}\)は\(\displaystyle \sigma \sqrt{\frac{T}{\mu}}\exp{(-\frac{E_\rm{a}}{RT})}[\rm{A}\)\(][\rm{B}]\)に比例することになります。
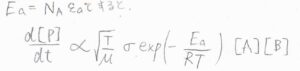
前半で予想したときに、反応に必要なエネルギーの最小値を一応\(E’\)と区別していたのですが、これは\(E_\rm{a}\)と同一のものとなります。
実験中の温度の範囲で、\(\displaystyle \exp{(-\frac{E_\rm{a}}{RT})}\)の変化に比べて、\(\sqrt{T}\)の変化が十分に小さければ、アレニウスの式が成り立つことになります。
アレニウスの式で、頻度因子は定数とされていましたが、分子論的に考えれば温度依存性があります。
立体因子
以上の考察から、理論上の反応速度\(k_\rm{calc}\)は、\(\sigma N_\rm{A}\)\(\displaystyle \sqrt{\frac{8k_\rm{B} \mathit{T}}{\pi \mu}}\exp{(-\frac{E_\rm{a}}{RT})}\)と書けます。
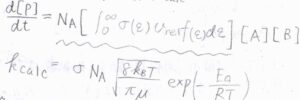
しかし、多くの場合、実際の反応速度定数\(k_\rm{obs}\)は、理論値\(k_\rm{calc}\)よりも数桁小さくなることが知られています。
これまでの考察で、分子は球であるとしていましたが、実際の多原子分子はもっと複雑な形状をしており、電子の疎密や立体反発の程度の違いで、活性の高い部分と低い部分があるはずです。
\(k_\rm{obs}\)と\(k_\rm{calc}\)の比は立体因子と呼ばれ、ここでは\(P\)と表すことにします。
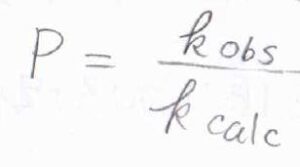

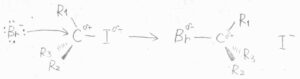
立体反発だけを反映しているわけではなくて、たとえば\(\rm{S_N}\)\(2\)反応のように、反応が起こる衝突の向きがある場合も反応が起こりにくくなるため、\(P\)は小さくなります。
ただ、\(P\)は\(1\)よりも大きくなることもあります。
代表的なのは、銛機構もしくは銛打ち機構と呼ばれる機構です。
銛(もり)とは、魚などを突き刺して捕まえる漁具のことです。
金属である\(\rm{K}\)とハロゲンの単体である\(\rm{Br}_2\)が反応して、\(\rm{KBr}\)と\(\rm{Br}\)が生成するという反応があります。
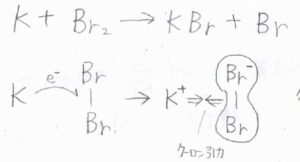
金属は、イオン化エネルギーが小さく、ハロゲンは電気陰性度が大きいため、\(\rm{K}\)と\(\rm{Br}_2\)が接近すると電子の受け渡しが起こります。
立て続けに、\(\rm{K}\)\(^+\)と\(\rm{Br}\)\(_2^-\)の間で静電引力が発生し、\(\rm{KBr}\)まで反応が進行します。
衝突するまで接近しなくても、電子を打ち込み相手を捕捉するさまを、銛で魚を突いて捕まえる様子に例えて、銛機構と言います。
こうなると、反応が起こるための見かけ上の衝突断面積が、実際の衝突断面積よりも大きくなるため、立体因子\(P\)は大きくなり、予想よりも速く反応が進行することになります。
RRKモデル
最後に、衝突では説明ができない\(1\)分子素反応について、RRK(Rice–Ramsperger–Kassel)モデルというものを紹介して終わります。
化学結合が複数ある多原子分子を、独立した複数の調和振動子の集まりとして考えます。
振動数はすべて同じ\(\nu\)として、\(1\)つの分子がもつ調和振動子の個数は\(s\)とします。
分子がもつエネルギーは\(nh\nu\)で、反応するために調和振動子がもつべき最小のエネルギーを\(n^\ast h\nu\)とします。
\(h\)はプランク定数です。
特定の化学結合にエネルギーが集中していれば、反応が起こるというイメージがわかりやすいかと思います。
\(s\)個の調和振動子に\(nh\nu\)のエネルギーを分配する場合の数\(N\)は、こちらの図を使って次のように考えます。
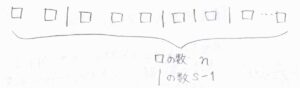
\(n\)個の四角があって、これに\(s-1\)本の仕切りを入れていきます。
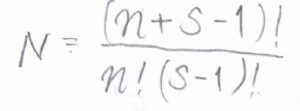
それぞれの四角と仕切りが区別できる場合、並べ方は\((n+s-1)!\)通りとなります。
実際には区別できないので、これを\(n!(s-1)!\)で割った値が\(N\)になります。
そして、少なくとも\(1\)つの調和振動子に\(n^\ast h\nu\)以上のエネルギーが分配される場合の数\(N^\ast\)は、\(\displaystyle \frac{(n-n^\ast+s-1)!}{(n-n^\ast)!(s-1)!}\)となります。
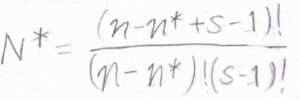
\(1\)つの調和振動子に\(n^\ast h\nu\)を分配しておき、さらに残りの\((n-n^\ast)h\nu\)を\(s\)個の調和振動子に割り当てます。
これは、\(n-n^\ast\)個の四角に\(s-1\)本の仕切りを入れる場合の数になります。
反応が起こる確率\(P’\)は、\(\displaystyle \frac{N^\ast}{N}\)となります。
\(N\)と\(N^\ast\)に先ほどの式を代入すると、\(P’\)はこのように書けます。
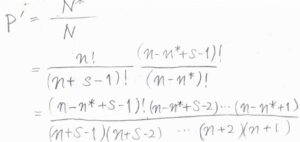
ここで、\(n-n^\ast\)が\(s\)に比べて十分に大きいとして近似すると、\(\displaystyle P’=(\frac{n-n^\ast}{n})^{s-1}\)と書けます。
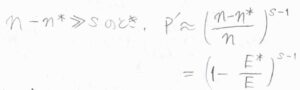
エネルギーを使って書くと、\(\displaystyle P’=(1-\frac{E^\ast}{E})^{s-1}\)というように、衝突断面積と似た式が出てきます。
横軸に分子がもつエネルギー\(E\)、縦軸に反応確率\(P’\)をとると、こちらのグラフのようになります。

\(s\)が小さいほど、特定の調和振動子にエネルギーが分配されやすいため、反応が起こりやすくなります。
また、調和振動子が多くても、全体のエネルギーが大きければ、反応に十分なエネルギーが分配されやすくなるため、反応確率は高くなります。
エネルギーが高くなるほど、反応速度は調和振動子の個数に影響されにくくなります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!