こんにちは!
今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(converted mass)
では参りましょう!
今回考えるモデル
まず、この動画で考えるのは二つの物体がばねで繋がれたこんなモデルです。
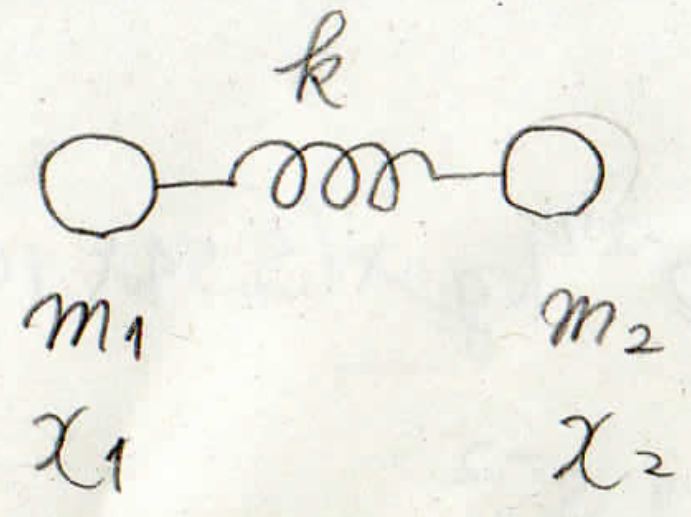
ばね定数が\(k\)、質量が\(m\)、位置が\(x\)です。
この系の重心はこのように与えられまして、重心から見た各物体の位置は\(r\)として考えることにします。
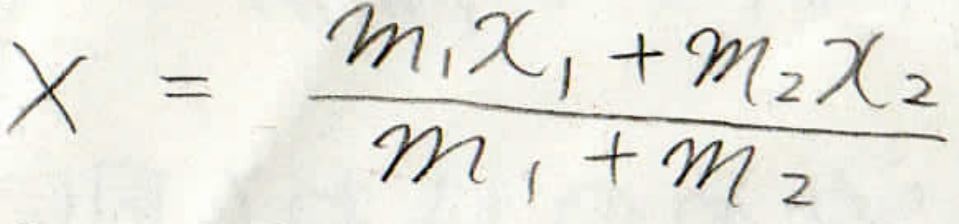
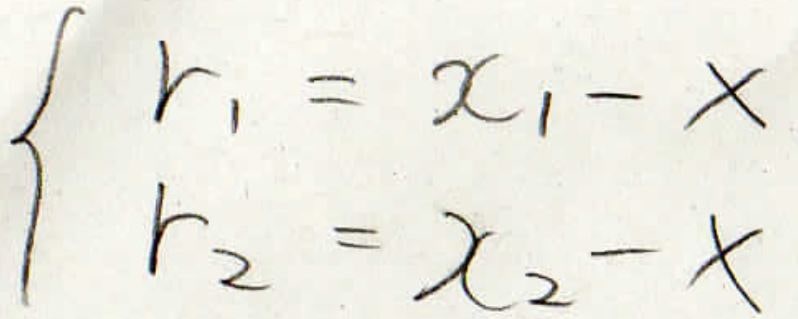
そして、重心から見た各物体の速さから全体の角運動量を考えたのが次の式になります。

重心の式を代入するとキャンセルして、結局運動量は\(0\)になります。
そのため、ばねで繋がれた系の運動量を考えるためには、重心についてのみ考えればよいということになります。
運動エネルギー
続いて、運動エネルギーを考えてみましょう。
これは重心から見たものではなくて、単純に全体の運動エネルギーを出したものです。
すると、\(x\)が\(r+X\)で書けることより、このようになります。
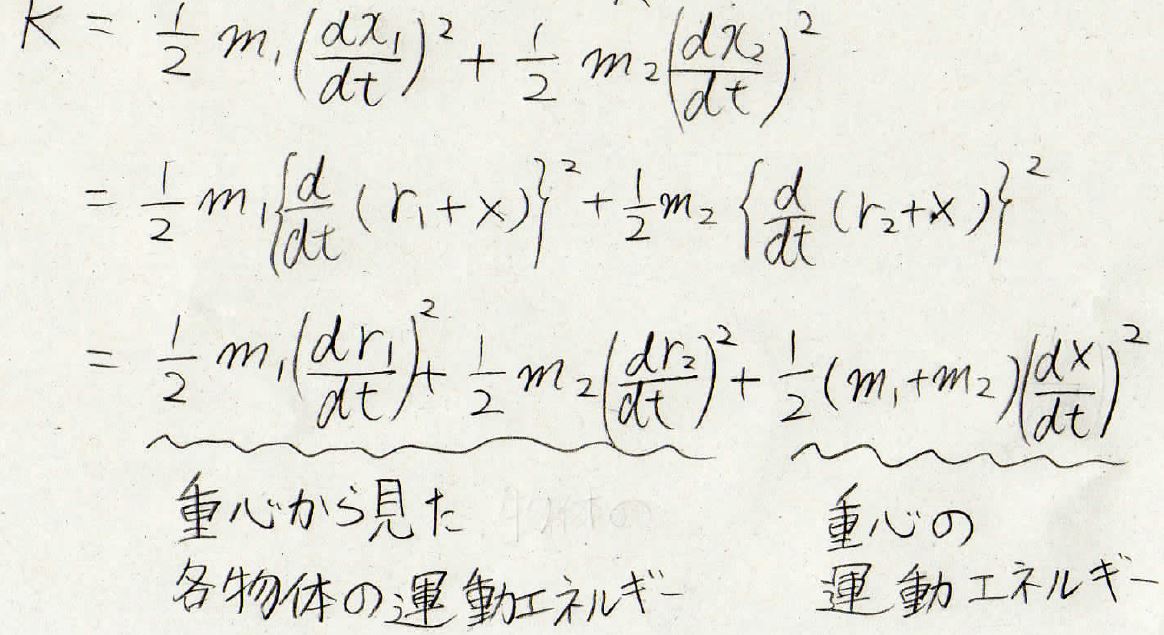
この式で第一項と第二項は重心から見たときの運動エネルギーになっていて、第三項目は重心だけの運動エネルギーになっています。
ここで二物体間の距離を添え字がついてない\(r\)として\(r_1\)と\(r_2\)を表すとこのようになります。
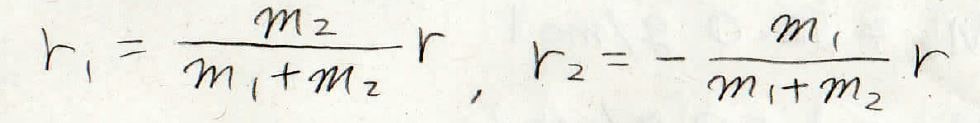
これを重心から見た運動エネルギーの式に入れると、1個の物体の調和振動という形になります。
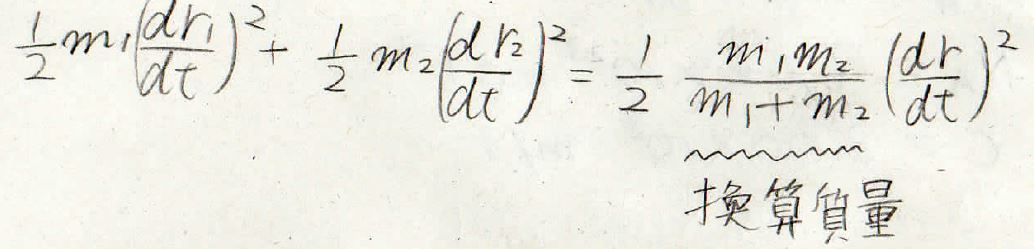
ただし、質量部分は少し複雑で\frac{m_1m_2}{m_1+m_2}というものになっています。
これは換算質量と呼ばれる値で、ここでは\(\mu\)で表すことにします。
換算質量
このように、それぞれの質量を逆数にして足すと、換算質量\(\mu\)の逆数になるという関係になっています。
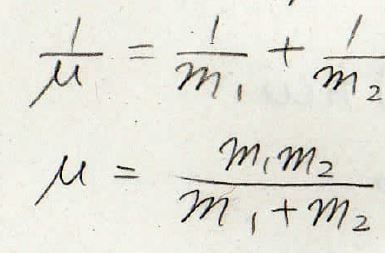
この換算質量を使うと、全体のエネルギーはこのように書けることになります。
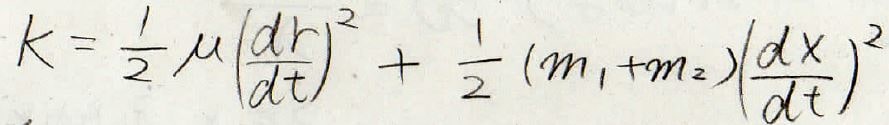
この式からわかることは、重心の運動を分離して考えると、二物体の運動は1つの物体の運動として考えることができるということです。
つまりは下図のように、片方が壁とか固定されているもので、物体が1個運動しているように見なすことができます。

この想像上の物体の質量こそが換算質量だということになります。
試しに重心を無視して単振動の式を考えると、ただの三角関数が得られることになります。
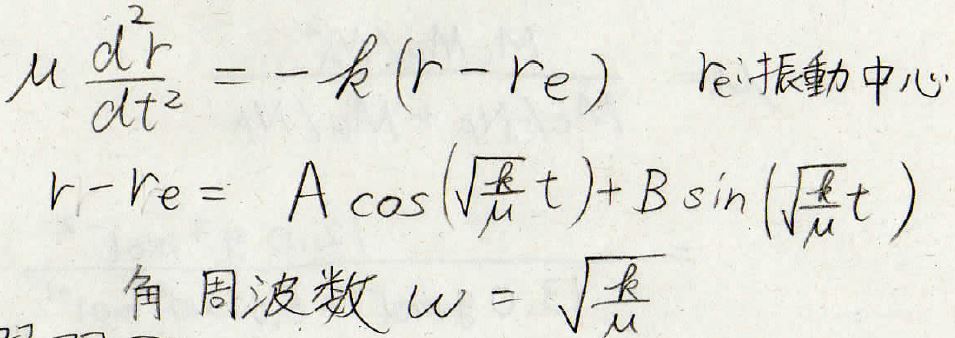
練習問題
では最後に、練習問題をやってみようと思います。
ここからは大学の内容が入ってくるのですが、12Cと1H間に単結合があったとして、その振動準位が\(3400\ \rm{nm}\)\(\)の赤外線を吸収するとともに励起されたとします。
このときにC-H結合の力の定数\(k\)はいくらになるでしょうかというのが問題です。
こちらが計算に使うパラメータになります。
\(M_\rm{C}\)\(\)、\(M_\rm{H}\)\(\)はそれぞれ炭素原子と水素原子のモル質量です。
\(N_\rm{A}\)\(\)はアボガドロ数、\(c\)は光の速さです。
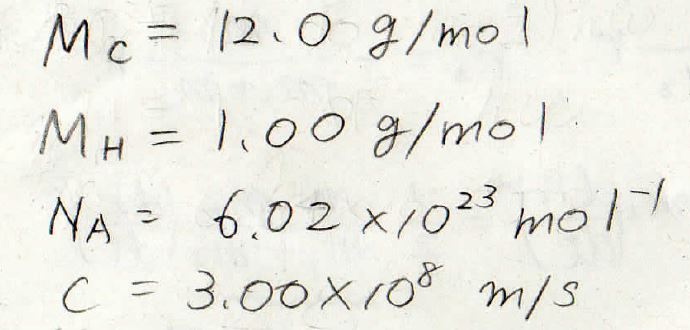

光子1個当たりのエネルギーは、プランク定数と振動数の積で与えられることから、この式が成り立つことになります。

それぞれ値を入れて計算することで、\(\omega\)が\(5.54×10^{14}\ \rm{rad\ s}^{-1}\) となることがわかります。
そして換算質量も求めると、\(1.53×10^{-24}\ \rm{g}\)になります。
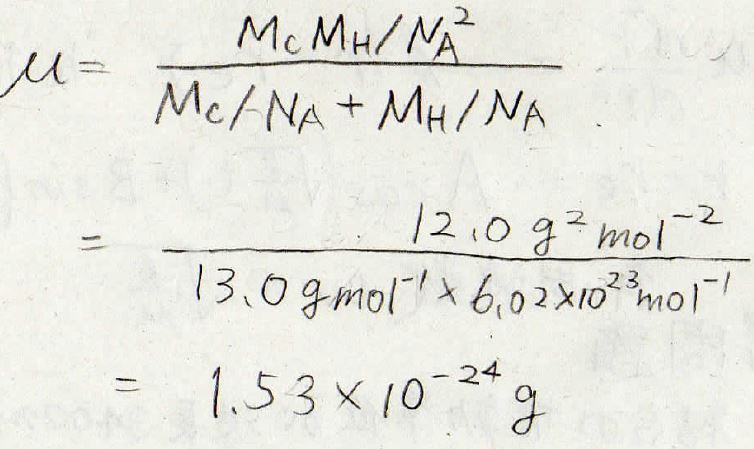
\(\omega=\sqrt{\frac{k}{\mu}}\)より、\(k=\mu \omega ^2\)となるので、あとは数値を代入すれば、\(470\ \rm{kg\ s}\)\(^{-2}\)という値が出てきます。
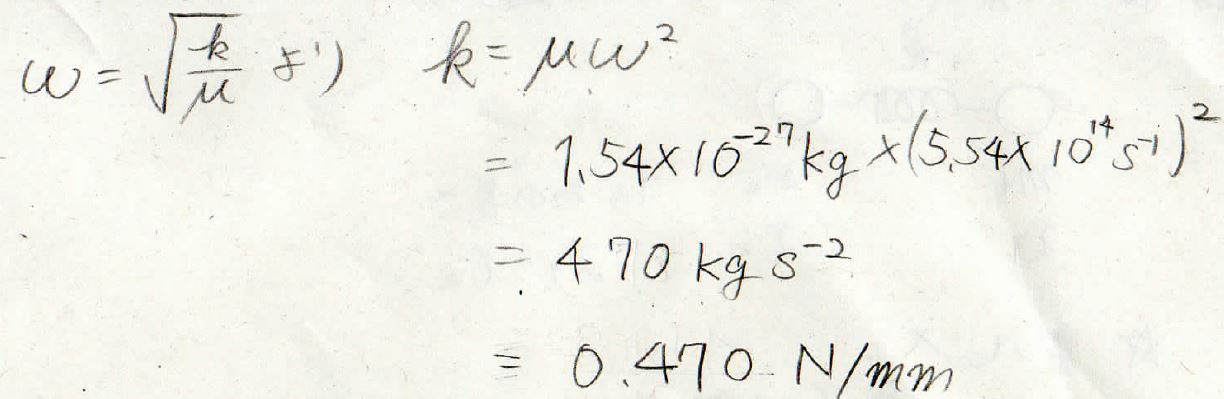
ばね定数は、SI単位系以外に\(\rm{N\ mm}^{-1}\)という単位もよく使われますが、それだと\(0.470\ \rm{N\ mm}^{-1}\)となります。
これは、よく売っているばねの中だと、比較的やわらかめのばねの値と同じくらいのようです。
まとめ
今回は、ばねで繋がれた二物体の運動の扱い方についてお話ししました。
換算質量を使ってあげることで、1つの物体の単振動とみなすことができるようになります。
そして全体の運動エネルギーは、この単振動のエネルギーと重心の運動エネルギーの和として分解することができます。
練習問題でやったように、振動準位の励起を考える際は重心の運動は関係ないので、換算質量だけで簡単に結合の固さを計算することができます。
今回は以上です。
それではどうもありがとうございました!



