こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(adsorption)
それでは内容に入っていきます!
ラングミュアの等温式
始めに、最も単純なラングミュア(Langmuir)の等温式というものから紹介します。
仮定
ラングミュアの等温式では、次の3つの仮定をしています。
まず、吸着質は単分子層までしか形成せず、単分子層に再び吸着が起こることはないものとします。
また、すべての吸着点は等価であり、どこで吸着が起こるのかは完全にランダムであるとします。
最後、吸着分子間で相互作用はなく、吸着エンタルピーは被覆率に依存しないものとします。
ここから、ラングミュアの等温式を導いていきます。
解離を伴わない場合
まず、吸着質を\(\rm{A}\)、吸着媒を\(\rm{M}\)として、こちらのような非解離性の化学吸着を考えます。

吸着と脱着の反応速度定数は、それぞれ\(k_\rm{a}\)、\(k_\rm{d}\)とします。
吸着速度は気体の圧力と空の吸着点の数に比例し、脱着速度は現在占められている吸着点の数に比例するため、被覆率\(\theta\)の変化速度\(\displaystyle \frac{\rm{d}\theta}{\rm{d}\mathit{t}}\)は、\(k_\rm{a}\)\(pN_\rm{sites}\)\((1-\theta)-k_\rm{d}\)\(N_\rm{sites}\)\(\theta\)と書けます。
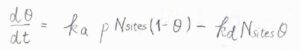
ここで、\(p\)は気体の圧力、\(N_\rm{sites}\)は吸着点の総数です。
動的な平衡状態に至ったとき、\(\displaystyle \frac{\rm{d}\theta}{\rm{d}\mathit{t}}=0\)を\(\theta\)について解くと、\(\displaystyle \theta=\frac{k_\rm{a}\mathit{p}}{k_\rm{a}\mathit{p}+\mathit{k}_\rm{d}}\)となります。
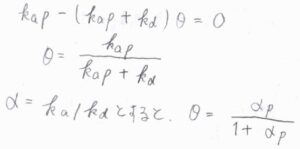
吸着と脱着の速度定数の比\(\displaystyle \frac{k_\rm{a}}{k_\rm{d}}\)を\(\alpha\)とすると、\(\displaystyle \theta=\frac{\alpha p}{1+\alpha p}\)とも書けます。
これが、解離を伴わない吸着についてのラングミュアの等温式です。
解離を伴う場合
対して、解離を伴う場合の吸着速度は、吸着速度は圧力のほか、すべてのフラグメントが空の吸着点を見つける確率に比例します。

また、脱着速度は必要な数のフラグメントが表面で出会う確率に比例します。
したがって、吸着質が2つのフラグメントに解離する場合、\(\displaystyle \frac{\rm{d}\theta}{\rm{d}\mathit{t}}=k_\rm{a}\)\(\{N_\rm{sites}\)\((1-\theta)\}^2-k_\rm{d}\)\((N_\rm{sites}\)\(\theta)^2\)と書けます。
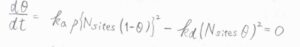
平衡状態に至ったとき、\(\displaystyle \frac{\rm{d}\theta}{\rm{d}\mathit{t}}=0\)とすると、\(\theta\)についての二次方程式となります。
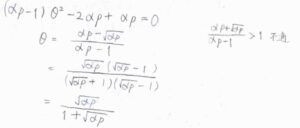
これを解くと、一方の解は\(1\)よりも大きく、被覆率として不適となるので、\(\displaystyle \theta=\frac{\sqrt{\alpha p}}{1+\sqrt{\alpha p}}\)と求められます。
これが吸着質が2つのフラグメントに解離する場合のラングミュアの等温式です。
以上の結果をグラフにすると、こちらのようになります。
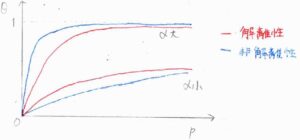
縦軸が平衡状態に至ったときの被覆率、横軸が圧力です。
赤い線が解離性化学吸着、青い線が非解離性化学吸着を表しています。
いずれの場合も、被覆率の高圧極限は\(1\)になるので、圧力が低い領域のほうが両者の違いはわかりやすいです。
まず、\(\alpha\)が小さいときには、解離性のほうがより多くの吸着点を占めることになります。
脱着の速度定数が大きくても、表面でフラグメントが出会わないと脱着できないため、解離性脱着は非解離性脱着よりも遅くなります。
一方、\(\alpha\)が大きいときには、非解離性のほうがより多くの吸着点を占めることになります。
被覆率が高いときに、空の吸着点を2つ見つけるのは困難であるため、解離性吸着は非解離性吸着よりも遅くなります。
平衡定数と標準吸着エンタルピー
吸着平衡の平衡定数\(K\)は、こちらのように定義されます。
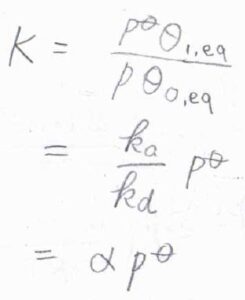
ここで、\(p^\circ\)は標準圧力、\(\theta_\rm{1, eq}\)は平衡状態における被覆率、\(\theta_\rm{0,eq}\)は平衡状態における空の吸着点の割合です。
速度定数を用いて表すと、\(\displaystyle K=\frac{k_\rm{a}}{k_\rm{d}}p^\circ\)となります。
先ほど導入した物理定数\(\alpha\)を使えば、\(K=\alpha p^\circ\)と書けます。
さらに、平衡定数と標準反応ギブズエネルギーの関係より、標準吸着ギブズエネルギー\(\Delta_\rm{ad}\)\( G^\circ=-RT\ln{(\alpha p^\circ)}\)と書けます。
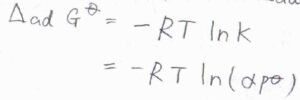
ここで、\(R\)は気体定数、\(T\)は絶対温度です。
これをギブズ-ヘルムホルツの式に代入すると、標準吸着エンタルピー\(\Delta_\rm{ad}\)\(\displaystyle H^\circ=RT^2[\frac{\partial \ln{(\alpha p^\circ)}}{\partial T}]_\theta\)と求められます。
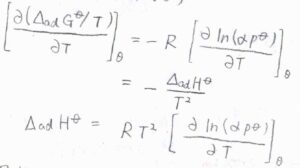
ギブズ-ヘルムホルツの式については、こちらを参照してください。

ラングミュアの等温式では、吸着エンタルピーが被覆率に依存しないことを仮定しているため、\(\alpha\)も被覆率に依存しません。
ただし、実際は依存することが多いため、ここでは偏微分の形で書いています。
吸着エンタルピーが被覆率に依存する理由には、吸着質間の相互作用もあるのですが、すべての吸着点が等価であるという仮定と現実との違いもあります。
実際には、活性の高い表面欠陥で優先的に吸着が起こるため、吸着エンタルピーは被覆率が高くなるにつれて、負に小さい値となっていきます。
BETの等温式
続いて、ブルナウアー(Brunauer)、エメット(Emett)、テラー(Teller)によって導かれたBETの等温式を紹介します。
先ほどのラングミュアの等温式では、単分子層吸着を考えていましたが、ここからは、吸着した分子にさらに分子が吸着していく多分子層吸着を考えていきます。
単分子層で占められた吸着点の割合を\(\theta_1\)、二重層で占められた吸着点の割合を\(\theta_2\)、\(\displaystyle \cdots\)と表すことにします。
解離を伴わない吸着について、吸着した分子の総数を\(N\)とすると、\(N=N_\rm{sites}\)\((\theta_1+2\theta_2+3\theta_3+\cdots)\)と書けます。
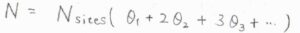
そして、第1層について、吸着速度は空の吸着点の数と圧力に比例し、脱着速度は単分子層で覆われた吸着点の数に比例するため、平衡状態で\(k_\rm{a, 0}\)\(p\theta_0=k_\rm{d, 0}\)\(\theta_1\)となります。
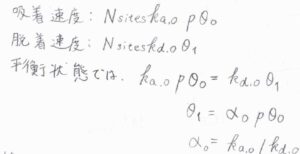
これを整理すると、\(\theta_1=\alpha_0p\theta_0\)という関係が得られます。
ここで、\(\alpha_0\)は第1層についての吸着と脱着の速度定数の比です。
同様に第2層について考えると、\(\theta_2=\alpha_1p\theta_1\)となります。

さらに、\(\theta_1=\alpha_0p\theta_0\)を代入すると、\(\theta_2=\alpha_0\alpha_1p^2\theta_0\)となります。
ここで、第1層の吸着は、吸着媒と吸着質の間で起こりますが、第2層以降の吸着は吸着質間で起こるため、そのエンタルピー変化は純粋な吸着質の凝縮エンタルピーに近い値となるはずです。
そこで、第3層以降も吸着と脱着の速度定数の比が第2層と等しくなると仮定します。
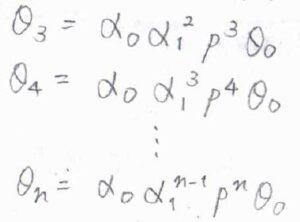
すると、\(\theta_n=\alpha_0\alpha_1^{n-1}p^n\theta_0\)と書けることになります。
すべての吸着点の割合を足したものは\(1\)になるはずなので、ここに以上の結果を代入すると、こちらのようになります。
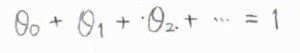
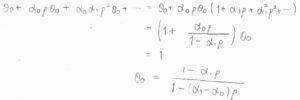
等比数列の無限級数の和を考えることで、\(\displaystyle (1+\frac{\alpha_0p}{1-\alpha_1p})\theta_0=1\)という式が得られます。
したがって、\(\displaystyle \theta_0=\frac{1-\alpha_1p}{1-(\alpha_1-\alpha_0)p}\)という形で、空の吸着点の割合が求められます。
先ほど出てきた、吸着した分子数\(N\)の式に\(\displaystyle \theta_0=\frac{1-\alpha_1p}{1-(\alpha_1-\alpha_0)p}\)を代入して整理すると、\(\displaystyle N=\frac{N_\rm{sites}\alpha_0\mathit{p}}{(1-\alpha_1p)[1-(\alpha_1-\alpha_0)p]}\)となります。

\(\displaystyle \frac{N}{N_\rm{sites}}\)は、ラングミュアの等温式で考えた被覆率に相当する量で、吸着している分子の量に相当する自由体積\(V\)を単分子層被膜に相当する体積\(V_\rm{mon}\)で除したものと一致します。
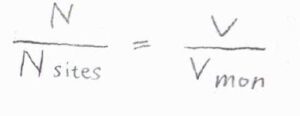
被覆率との違いは、圧力が高いときに\(1\)を超えて大きくなるということです。
そして、これは繰り返しになりますが、第1層以外の吸着および脱着は気化と同じように考えることができるので、平衡状態で\(k_\rm{a, 1}\)\(p^\ast=k_\rm{d, 1}\)となります。
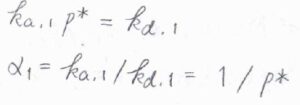
ここで、\(p^\ast\)は飽和蒸気圧です。
このことより、\(\displaystyle \alpha_1=\frac{1}{p^\ast}\)とも書けます。
\(\displaystyle \frac{p}{p^\ast}\)を\(z\)、\(\displaystyle \frac{\alpha_0}{\alpha_1}\)を\(c\)とすると、\(\displaystyle \frac{V}{V_\rm{mon}}=\frac{cz}{(1-z)[1-(1-c)z]}\)と変形できます。
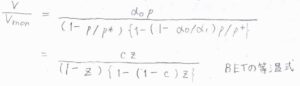
この式をBETの等温式と言います。
縦軸を\(\displaystyle \frac{V}{V_\rm{mon}}\)、横軸を\(z\)とすると、こちらのグラフのようになります。
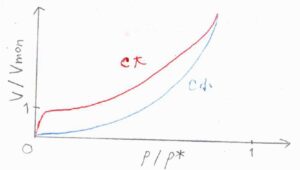
赤い線は\(c\)が大きいとき、青い線は\(c\)が小さいときの概形を表しています。
まず、\(c\)が大きいとき、すなわち凝縮よりも1層目の吸着が起こりやすい場合、圧力が低くても\(\displaystyle \frac{V}{V_\rm{mon}}=1\)までは簡単に吸着が起こります。
\(c\)がとても大きいとすると、\(\displaystyle \frac{V}{V_\rm{mon}}\approx \frac{1}{1-z}\)と近似できるように、圧力がある程度高い領域では、反比例のグラフを平行移動した形に近くなります。
一方、\(c\)が小さい場合、すなわち1層目の吸着よりも凝縮が起こりやすい場合は、\(\displaystyle \frac{V}{V_\rm{mon}} \approx 1\)までのジャンプもなく、圧力が高くなって第1層の吸着が起こるようになれば、それをきっかけとして多くの分子が吸着して、\(\displaystyle \frac{V}{V_\rm{mon}}\)が跳ね上がっていく形となります。
実際に、あらゆる圧力、物質の組み合わせで実験結果を説明できるというわけではありませんが、固体の表面積を求めるために、産業界では広く使われています。
ここで再度、平衡定数について考えてみましょう。
まず第1層について、標準吸着ギブズエネルギー\(\Delta_\rm{ad}\)\( G^\circ\)と標準脱着ギブズエネルギー\(\Delta_\rm{des}\)\( G^\circ\)は逆符号になるため、平衡定数\(\displaystyle \alpha_0p^\circ=\exp{(-\frac{\Delta_\rm{ad} \mathit{G^\circ}}{RT})}=\exp{(\frac{\Delta_\rm{des} \mathit{G^\circ}}{RT})}\)と表されます。
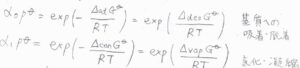
同様に、2層目以降の吸着について、標準凝縮ギブズエネルギー\(\Delta_\rm{con}\)\( G^\circ\)と標準蒸発ギブズエネルギー\(\Delta_\rm{vap}\)\( G^\circ\)も逆符号になるため、平衡定数\(\displaystyle \alpha_1p^\circ=\exp{(-\frac{\Delta_\rm{con} \mathit{G^\circ}}{RT})}=\exp{(\frac{\Delta_\rm{vap} \mathit{G^\circ}}{RT})}\)となります。
先ほどの変数\(\displaystyle c=\frac{\alpha_0}{\alpha_1}\)より、\(\displaystyle c=\frac{\exp{(\Delta_\rm{des} \mathit{H^\circ/RT})}\exp{(-\Delta_\rm{des} \mathit{S^\circ/R})}}{\exp{(\Delta_\rm{vap} \mathit{H^\circ/RT})}\exp{(\Delta_\rm{vap} \mathit{S^\circ/R})}}\)と書けます。
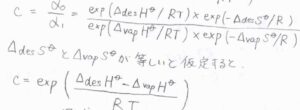
ここで、脱着も気化も自由に並進運動ができるようになる変化であることから、そのエントロピー変化も同程度であると考えられます。
両者が等しいと仮定すると、\(\displaystyle c=\exp{[\frac{\Delta_\rm{des} \mathit{H^\circ}-\Delta_{vap} \mathit{H^\circ}}{RT}]}\)となります。
テムキンの等温式、フロイントリッヒの等温式
最後、ラングミュアの等温式やBETの等温式では考慮できない影響を考えるために提案された等温式について、少しお話して終わります。
まず、その考慮できない影響というのは、吸着点が互いに独立であり等価であるという仮定が成り立たないことによるものです。
つまり、現実には表面欠陥がある吸着点が優先的に占められますし、吸着質どうしの相互作用も吸着する量に影響を及ぼします。
吸着媒の結晶面によって、吸着しやすさが変わるということも珍しくありません。
こちらのテムキンの等温式では、吸着エンタルピーが圧力に対して直線的に変化することを仮定して、被覆率が圧力の対数として書けるものとしています。

フロイントリッヒの等温式では、吸着エンタルピーが圧力に対して対数的な変化をすることを仮定したことで、被覆率と圧力の間にべき乗則が成り立つものとしています。
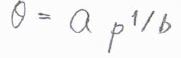
これらの等温式は、限られた圧力範囲において実験結果とよく合わせることができますが、用いた仮定の根拠に欠いており、ほぼ経験的なものです。
しかし、それぞれのフィッティングパラメータによって、種々の条件下における不均一触媒作用についても、ある程度信頼できる予測ができるため、経験的といっても、まったく無駄というわけではなくて、必要な情報として扱われています。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




