こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(diffusion)
それでは内容に入っていきます!
熱力学的な解釈
まず、拡散という現象は、熱力学第二法則を使って解釈することができます。
熱力学第二法則については、こちらを参照してください。

一度巨視的に均一となった溶液が、手を加えずに再び溶媒と溶質に別れることはありません。
拡散は、孤立系として見たときのエントロピーが増大する方向へ起こります。
単成分系において、温度と圧力が一定のとき、体積変化を伴わない仕事の最大値\(w_\rm{add, max}\)\(\)は、ギブズエネルギーの変化量\(\Delta G\)となります。
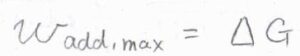
最大仕事については、こちらを参照してください。

これを微少量として書き、また混合物中における部分モル量にすることを考えると、最大仕事\(\rm{d’}\)\(w_\rm{e}\)\(=\rm{d}\)\( \mu\)と書けます。
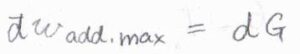
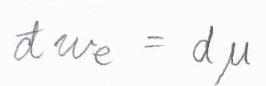
いま、この仕事は溶質が散逸するために必要な仕事を指していると考えてください。
\(\mu\)は部分モルギブズエネルギー、すなわち化学ポテンシャルです。
もし、ある時刻において、化学ポテンシャルが位置\(x\)に依存するとき、\(\rm{d’}\)\(w_e=(\partial \mu/\partial x)_{T, p}\rm{d}\)\(x\)と書けます。
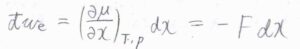
仕事は力の大きさと移動した距離の積であることから、\((\partial \mu/\partial x)\)が力の大きさ\(F\)に相当することがわかります。
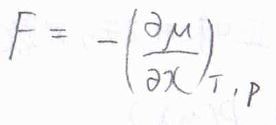
ただし、この力の大きさは、あくまで溶質分子が分散する傾向を、力の単位で表したものに過ぎず、実際に個々の溶質分子が同じ大きさの力を受けているというわけではありません。
またここでは、外部から系へされた仕事を正としている都合上、\(F\rm{d}\)\(x\)の前にはマイナスが付きます。
溶質の活量を\(a\)として、化学ポテンシャルと活量の関係式を使うと、\(F=-RT[\partial (\ln{a}/\partial x)]_{T, p}\)と書けます。
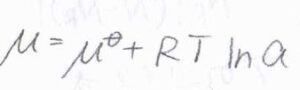
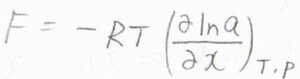
ここで、\(R\)は気体定数、\(T\)は絶対温度です。
活量係数が\(1\)と仮定すると、モル濃度を\(c\)として、\(F=-(RT/c)(\partial c/\partial x)_{T, p}\)と書けます。
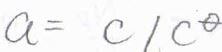
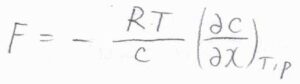
整理すると、\((\partial c/\partial x)_{T, p}=-cF/RT\)となります。
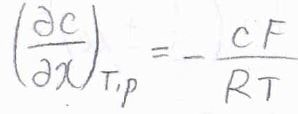
ここで、前々回の記事で紹介したフィックの第一法則を使います。
物質輸送の流束が濃度勾配に比例するというもので、このような式が成り立ちます。

ここで、\(J\)は溶質分子の流束、\(N\)は溶質分子の数密度で、比例定数である\(D\)は拡散係数と呼ばれます。
溶質分子は濃度が濃いところから薄いところへ拡散していくため、マイナスの符号が付きます。
溶質の物質量の流束を\(J’\)とすると、これは数密度をモル濃度に変換することで、\(-D(\rm{d}\)\(c/\rm{d}\)\(x)\)と書けます。
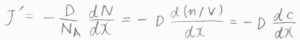
また、流束の定義より、ドリフト速さ\(s\)を使うと、\(J’=sc\)とも書けます。
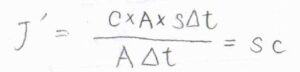
以上の関係を整理すると、\(sc=DcF/RT\)となることから、ドリフト速さ\(s=DF/RT\)という関係が導かれます。
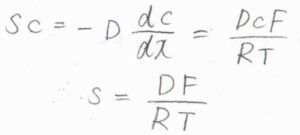
この関係は、記事の終盤で使います。
フィックの法則による解釈
続いて、フィックの第一法則で、濃度の時間変化を考えるというアプローチで拡散を考えてみます。
仮想的な窓の面積を\(A\)として、厚さ\(\lambda\)の直方体の中にある溶質分子のモル濃度の時間変化を考えます。
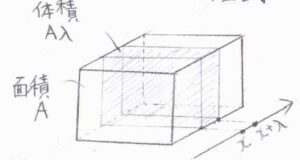
物質量の流束を\(J\)とすると、単位時間あたりにこの領域へ流入する溶質の物質量は\(J(x)A\)、外部へ流出する溶質の物質量は\(J(x+\lambda)A\)となります。
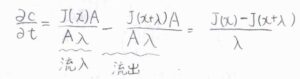
したがって、\(\partial c/\partial t\)は、これら物質量の差を体積\(A \lambda\)で割って、\([J(x)-J(x+\lambda)]/\lambda\)と書けます。
\(\lambda\)がとても小さいとして、\(c(x+\lambda)とc(\lambda)\)の関係が下のような関係で書けるとすると、フィックの第一法則より、\(J(x)-J(x+\lambda)=D \lambda(\partial^2 c/\partial x^2)\)となります。
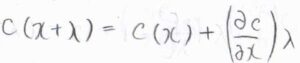

ただし、ここでは拡散係数の時間変化がないか、無視できるほど小さいとしています。
以上のことより、\(\partial c/\partial t=D(\partial^2 c/\partial x^2)\)という関係が導かれます。

これをフィックの第二法則または拡散方程式といいます。
図を使って、説明すると次のようになります。
まず濃度勾配が一定のとき、流入してくる分子の量と流出していく分子の量が等しいため、時間が経ってもその位置における濃度は一定となります。

対して、濃度勾配が変化するときには、位置を変数とした関数として見た濃度が上に凸のとき、流入量よりも流出量が多くなり、濃度は時間経過とともに小さくなります。
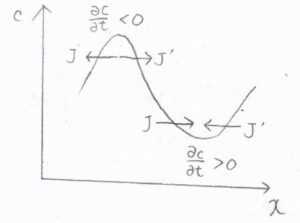
反対に、濃度が下に凸となる位置では、時間経過とともに濃度は大きくなります。
拡散が起こっている間、この過程が繰り返されることで、濃度の曲率は\(0\)に近づいていきます。
一般化
ところで、拡散方程式の中には、対流の項が入っていることがあります。
対流とは、流れている流体の運動から生じる粒子の輸送のことです。
流れるプールのように、全体が一定の速さで流れているとき、粒子の拡散運動もそれに影響を受けるイメージです。
対流のみによる物質量流束を\(J_\rm{conv}\)\((x)\)として、先ほどと同様の近似をすると、拡散方程式における対流の項が\(-v(\partial c/\partial x)\)となります。
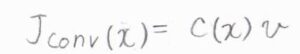

このように、式の適用できる範囲を広げることは、一般化といいます。
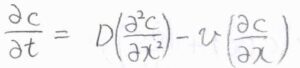
解の例
拡散方程式は、位置に関して二階、時間に対して一階の微分方程式であり、これを解くためには、2つの境界条件と1つの初期条件が必要になります。
ここでは、比較的簡単に解ける条件とその解を紹介します。
対流がない系において、時刻\(0\)ではすべての粒子が\(x=0\)の地点にあるとします。
つまり、時刻\(0\)における濃度は、ディラックのデルタ関数の形になります。
さらに、粒子の全物質量は\(n_0\)で一定であり、すべての物理量について\(x\rightarrow\pm \infty\)の極限が\(0\)に収束するという境界条件を設定します。
このときの解は、\(c(x,t)=[n_0/2(\pi Dt)^{1/2}]\exp{(-x^2/4Dt)}\)となります。
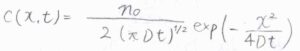
これは、一次元の結果ですが、同様の条件について三次元で考えた場合は、まず拡散方程式の右辺に\(\boldsymbol{\nabla}^2\)が出てきます。
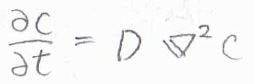
極座標にして考えれば、角度依存性はないので、変数は\(r\)と\(t\)の2つだけになって、解も\(c(r,t)=[n_0/8(\pi Dt)^{3/2}]\exp{(-r^2/4Dt)}\)という形になります。
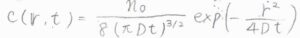
縦軸に濃度、横軸に原点からの距離\(r\)をとってグラフを書くと、こちらのようになります。
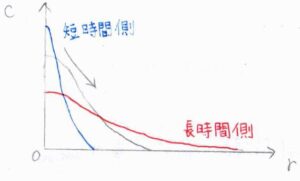
ガウス関数の形なので、\(r=0\)で濃度は最大値をとります。
そして、時間が経つにつれて、原点からより遠く離れた地点まで粒子が拡散するとともに、\(r=0\)の位置での濃度は減少していきます。
平均二乗変位(MSD)
時間が\(t\)だけ経過する間に、粒子が進む距離の二乗の平均は平均二乗変位、略してMSD(Mean-Square Displacement)と呼ばれ、その粒子がどれぐらい広がったのかを知る尺度としてしばしば使われます。
移動距離そのものの平均でなく、わざわざ二乗の平均をとるのは、原点から両方向へ拡散が起こるときに移動距離の平均が常に\(0\)となってしまうためです。
三次元におけるMSDは、こちらのように\(r^2\)の期待値を考えることで、\(6Dt\)となります。
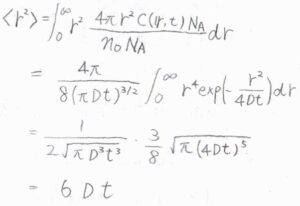
MSDは拡散運動の次元に比例するので、一次元の拡散では\(2Dt\)、二次元の拡散では\(4Dt\)となります。
そして、MSDの平方根を移動距離の目安と考えると、たとえば、拡散係数が\(10^{-10}\ \rm{m^2\ s}\)\(^{-1}\)のときに、粒子が\(1\ \rm{mm}\)\(\)進むために30分弱もかかることになります。
一般的に、粒子の拡散は非常に遅い過程であり、対流がある場合はそちらが粒子の運動に大きな影響を及ぼします。
たとえば、高濃度の食塩水を作りたいときに、攪拌する場合と攪拌しない場合では、すべて溶けきるまでにかかる時間に大きな差が生じます。
統計力学的な解釈
次に、統計力学的な考え方で拡散を考えていきます。
まず、一次元の酔歩モデルを考えます。

時間が\(\tau\)経過するごとに、\(\lambda\)だけ移動した点に移る過程を1ステップとして、これを繰り返す粒子があったとします。
正の方向へ動く確率と負の方向へ動く確率は等しく、コインを投げて表裏で決めるとします。
全体のステップ数\(N\)は、右に進んだ回数\(N_\rm{R}\)\(\)と左に進んだ回数\(N_\rm{L}\)\(\)の和であり、正味のステップ数\(N_\rm{R}\)\(-N_\rm{L}\)\(\)を\(n\)とおきます。
粒子が\(x=n\lambda\)にある確率を\(P(n\lambda)\)とすると、反復試行であることから\(P(n\lambda)=N!/[N_\rm{R}\)\(!(N-N_\rm{R}\)\()!]\times (1/2)^N\)となります。
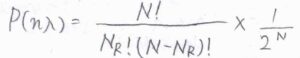
大きな整数の階乗があるので、そのまま計算することはほぼ不可能です。
そこで、スターリング展開の式を利用して、十分大きな\(x\)について\(\ln{x!}\)が\(x\ln{x}-x+(1/2)\ln{(2\pi x)}\)と近似できるものとします。

さらに、式を簡単な形にするために\(N_\rm{R}\)\(/N-1/2\)をパラメータ\(\mu\)とおきます。
\(N_\rm{R}\)\(/N\)はステップを重ねるごとに\(1/2\)に収束していくはずなので、\(\mu\)は\(0\)に近い値と考えることができます。
このとき、マクローリン展開を使って、\(\ln{(1/2\pm \mu)}=-\ln{2}\pm 2\mu-2\mu^2\)と近似できます。
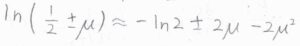
真数の\(1/2\pm \mu\)は、\(N_\rm{R}\)\(/N\)、\(N_\rm{L}\)\(/N\)と同じです。
ここから、再び\(P(n\lambda)\)を変形していきます。
まず大きな整数の階乗を外すために、\(P(n\lambda)\)の自然対数をとって、これを\(\mu\)を使って表すと、このような形になります。
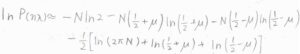
ここで、\(N_\rm{R}\)\(=N(1/2+\mu)\)、\(N_\rm{L}\)\(=N(1/2-\mu)\)です。
さらに、マクローリン展開を用いた近似をすると、\(P(n\lambda)=\ln{2}-(1/2)\ln{(2\pi N)}-2(N-1)\mu^2\)となります。
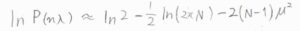
対数を外すと、\(P(n\lambda)=(2/(2\pi N)^{1/2})\exp{(-2N\mu^2)}\)となります。
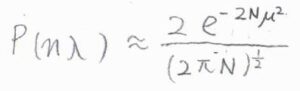
最後に、パラメータ\(\mu\)を消去すると、指数の\(N\mu^2\)は\(n^2/4N\)と書けます。
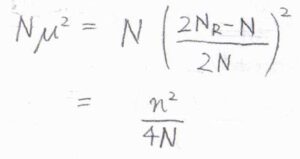
さらに、ステップ数\(N\)は実際の移動時間を1ステップあたりの時間\(\tau\)で割った値であり、正味のステップ数\(n\)は実際の粒子の位置\(x\)を1ステップあたりに進む距離\(\lambda\)で割った値であるため、粒子の存在確率\(P(x, t)\)は、\((2\tau/\pi t)^{1/2}\exp{(-\tau x^2/2t\lambda^2)}\)と書けます。
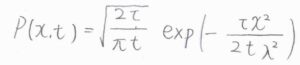
この式を先ほど紹介した拡散方程式の解と照らし合わせると、\(\tau/2t\lambda=1/4Dt\)となることから、拡散係数\(D=\lambda^2/2\tau\)という関係が導かれます。
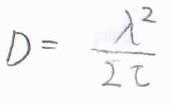
この式はアインシュタイン-スモルコフスキーの式と呼ばれ、粒子の運動の微視的な挙動と巨視的な拡散に関するパラメータを結びつける式です。
たとえば、\(\lambda/\tau\)を平均の分子の平均速さ\(\bar{v}\)、平均自由行程をステップ長\(\lambda\)と考えれば、\(D=(1/2)\bar{v}\lambda\)となって、理想気体の拡散係数\((1/3)\bar{v}\lambda\)と似た形になります。
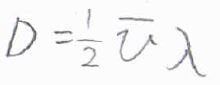
係数の違いは、平均自由行程よりも長い距離の分子輸送を排除しているかどうかの違いなので、本質的には同じ式になります。
このことから、理想気体分子の拡散は、ステップの大きさが平均自由行程と等しい酔歩と考えることができます。
ストークス-アインシュタインの式
熱力学第二法則から導かれたドリフト速さの式は、前回考えたイオンの式を照らし合わせることで、拡散係数についての重要な式を導くことができます。
イオン伝導率、移動度については、こちらを参照してください。

まず、電圧を印加されたイオンにかかる力の大きさは、電荷と電場の大きさの積であることから、ドリフト速さ\(s=zDFE/RT\)と書けます。

ここで、\(z\)はイオンの価数、\(E\)は電場の大きさです。
ここの\(F\)は力の大きさではなくファラデー定数を指すことに注意してください。
さらに、移動度の定義より、ドリフト速さsは移動度\(u\)と電場の大きさ\(E\)の積としても書けます。
電場の大きさ\(E\)を消去して整理すると、\(u=zDF/RT\)と表せることになります。
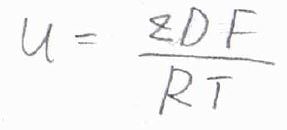
この関係をアインシュタインの関係といいます。
この関係を利用すると、イオン伝導率\(\lambda=zuF\)より\(\lambda=z^2DF^2/RT\)となります。
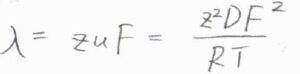
そして、濃度を\(0\)まで希釈していったとき、全体のモル伝導率の極限\(\Lambda_\rm{m}\)\(^\circ\)は、イオンの独立移動の法則より、\((\nu_+z_+^2D_++\nu_-z_-^2D_-)(F^2/RT)\)と書けます。
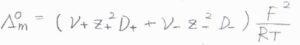
これをネルンスト-アインシュタインの式といいます。
ただし、\(\nu\)は溶質の化学式単位中にあるイオンの個数です。
この式を使うと、電気伝導率の測定からイオンの拡散係数を計算することができます。
さらに、イオンが球の形であるとすると、移動度\(u=ze/6\pi\eta a\)とも書けるので、こちらの等式の両辺を\(ze\)で割ると、\(D/k_\rm{B}\)\(T=1/6\pi \eta a\)となります。
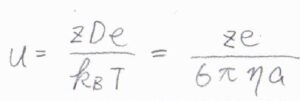
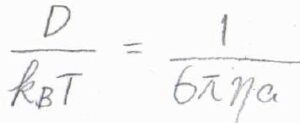
ここで、\(e\)は電気素量、\(k_\rm{B}\)\(\)はボルツマン定数、\(\eta\)は媒質の粘性率、\(a\)はイオンの流体力学的半径です。
この式を拡散係数\(D\)について整理すると、\(D=k_\rm{B}\)\(T/6\pi \eta a\)となります。
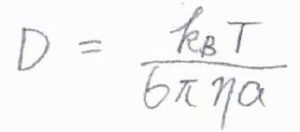
これをストークス-アインシュタインの式といいます。
電荷を消去できていることから、この式は電気的に中性な粒子についても適用することができます。
拡散方程式のところで、MSDと拡散係数の関係をお話ししましたが、たとえば、粒子の運動を光学的な手法でトラックしてMSDが計算できれば、拡散係数がわかって、粘度と流体力学的半径の積\(\eta a\)も計算できます。
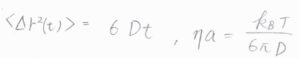
媒質の粘度を別の測定法で調べたり、文献値を使ったりすれば、流体力学的半径も個別に計算できます。
一般化
これは余談ですが、拡散係数と粘度を複素数として一般化すると、媒質がニュートン流体ではなく、時間によって力学特性が変化する粘弾性体についても適用することができると理論上考えられています。
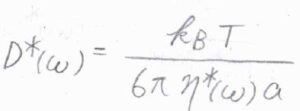

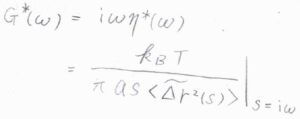

ニュートン流体中ではMSDは経過時間に比例しますが、粘弾性体中では媒質がもつ弾性が影響することで、経過時間にかかる指数が\(0\)から\(1\)までの範囲で時間変化します。
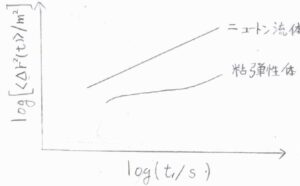
その指数の変化から粒子の周りにある分子の運動にかかる時間の目安がわかるというしくみです。
ただ、この式を使って計算した結果が力学的な測定の結果に一致する例と一致しない例がどちらも報告されているので、まだまだ検証が必要とされています。
実は、僕が研究していたのも、このマイクロレオロジーといわれる分野だったので、今回はついでに紹介してみました。
学部生には難しいかもしれませんが、また興味があれば調べてみてください。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!