こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Arrhenius equation)
それでは内容に入っていきます!
素反応
ここでは、ハロアルカンの求核置換反応を例にお話ししていきます。
嵩高くない第一級ハロアルカンに求核剤を加えると、求核攻撃と脱離基の脱離が協奏的、立体特異的に進行します。
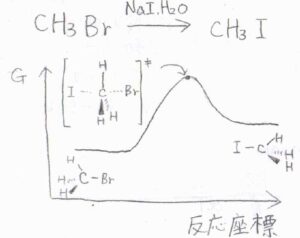
2つの分子が十分に接近することで、1ステップでこの反応が起こります。
これを二分子求核置換反応、通称\(\rm{S_N}\)\(2\)反応と言います。
対して、嵩高い第三級ハロアルカンに求核剤を加えると、その立体障害のために、求核攻撃しにくく、脱離基の脱離のほうが速く進行します。
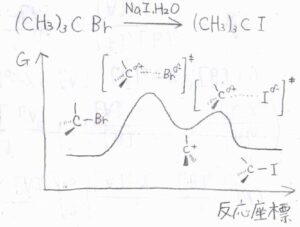
熱力学的にも安定な第三級カルボカチオン中間体ができます。
そこに求核攻撃が起こることで生成物ができるという2ステップの反応になります。
カルボカチオンが生成する段階には、求核剤は関与しておらず、これを一分子求核置換反応、通称\(\rm{S_N}\)\(1\)反応と言います。
平面構造のカルボカチオンを経由すると、立体の情報が保持されないので、キラルな基質を用いた場合の生成物はラセミ混合物になります。
ここで、反応の各ステップのことを素反応と言います。
過去の記事でも言ってきたとおり、全体の化学反応式から反応速度式を立てることはできませんが、素反応については立てることができます。
一分子素反応は\(1\)次反応になり、二分子素反応は\(2\)次反応になります。
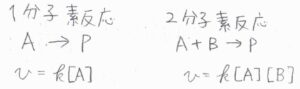
全体の反応次数は、一連の素反応のすべてを合算して決まります。
逐次素反応
では、簡単な例としてここでは逐次素反応、特に逐次\(1\)次反応を取り上げてみます。
正確には化学反応ではないですが、放射壊変が最もイメージしやすいと思います。
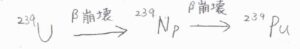
これは、原子力発電のために用いるプルトニウムを得る過程の一部ですが、放射性核種のウラン\(239\)が\(\beta\)崩壊して電子を放出すると、ネプツニウム\(239\)となり、さらに\(\beta\)崩壊してプルトニウム\(239\)となります。
このように、それぞれの素反応が\(1\)次反応で、かつ逆反応が起こらない反応について、反応速度式を立ててみます。
一般化して、反応物を\(\rm{A}\)、中間体を\(\rm{I}\)、生成物を\(\rm{P}\)、\(1\)段階目と\(2\)段階目の反応速度定数をそれぞれ\(k_1\)、\(k_2\)とします。

すると、\(\displaystyle \frac{\rm{d}[\rm{A}]}{\rm{d}\mathit{t}}=-k_1[\rm{A}]\)、\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}=k_2[\rm{I}]\)となります。
中間体については、生成と消滅が同時に起こるため、\(\displaystyle \frac{\rm{d}[\rm{I}]}{\rm{d}\mathit{t}}=k_1[\rm{A}\)\(]-k_2[\rm{I}]\)となります。
反応開始時点では\(\rm{A}\)しか存在しておらず、その初濃度を\([\rm{A}\)\(]_0\)とすると、\(\rm{A}\)と\(\rm{I}\)と\(\rm{P}\)のモル濃度の和が\([\rm{A}\)\(]_0\)になります。
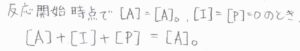
まず、\([\rm{A}]\)はすぐに計算できて、\([\rm{A}\)\(]_0\exp{(-k_1t)}\)とわかります。
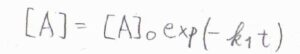
これを\(\rm{I}\)についての反応速度式に当てはめると、このようになります。
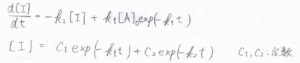
この解は、\(C_1\)と\(C_2\)を定数として、\(C_1\exp{(-k_1t)}+C_2\exp{(-k_2t)}\)で与えられます。
時刻\(0\)では、\([\rm{I}\)\(]=0\)であるため、\(C_1+C_2=0\)です。
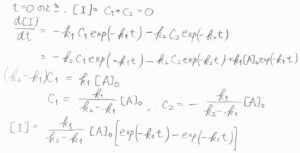
そして、\(\displaystyle \frac{\rm{d}[\rm{I}]}{\rm{d}\mathit{t}}\)を右辺と照らし合わせると、\((k_2-k_1)C_1=k_1[\rm{A}]_0\)という関係であることがわかるので、\(\displaystyle C_1=\frac{k_1[A]_0}{k_2-k_1}\)、\(\displaystyle C_2=-\frac{k_1[A]_0}{k_2-k_1}\)と出てきます。
したがって、\([\rm{I}\)\(\displaystyle ]=k_1\frac{[\rm{A}]_0}{k_2-k_1}[\exp{(-k_1t)-\exp{(-k_2t)}}]\)と書けます。
最後、\([\rm{P}\)\(]=[\rm{A}\)\(]_0-[\rm{A}\)\(]-[\rm{I}]\)より、\([\rm{P}\)\(]=[\rm{A}\)\(\displaystyle ]_0[1-\frac{k_2\exp{(-k_1t)}-k_1\exp{(-k_2t)}}{k_2-k_1}]\)となります。
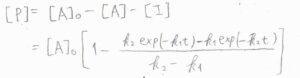
横軸を時刻\(t\)、縦軸をそれぞれのモル濃度としてグラフを書くと、このような概形になります。
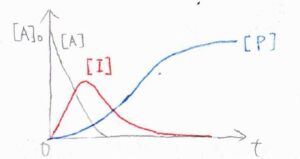
黒が\(\rm{A}\)、赤が\(\rm{I}\)、青が\(\rm{P}\)のモル濃度です。
このグラフは、\(1\)段階目の反応が\(2\)段階目よりも速く進行するときの概形で、中間体の\(\rm{I}\)でいる時間が長く、モル濃度の最大値も大きくなります。
\(2\)段階目の方が速い場合については、次の記事で詳しく扱います。
アレニウスの式
そして、反応速度定数の温度依存性を表した式として、アレニウスの式があります。
これは、理論ではなく実験的に得られたものです。
アレニウスの式は、反応速度定数の対数が絶対温度の逆数についての一次関数になるというものです。
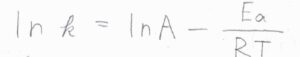
この式で、\(R\)が気体定数、\(T\)が絶対温度です。
\(A\)と\(E_\rm{a}\)は、実験的に決められる定数で、アレニウスパラメータと呼ばれます。
また、それぞれは頻度因子(前指数因子)、活性化エネルギーという個別の名前が付いています。
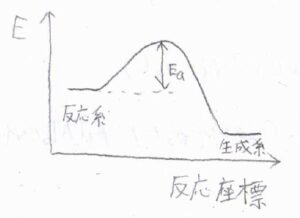
活性化エネルギーは、反応が起こるために必要な最小のモルあたりのエネルギーで、このようなポテンシャル図では、反応物と遷移状態のエネルギー差として説明されます。
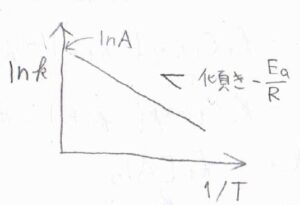
横軸に絶対温度の逆数、縦軸に反応速度定数の自然対数をとったグラフ(アレニウスプロット)は、同一直線上の点の集合となり、その傾きと切片から2つのアレニウスパラメータが決定されます。
これらの定数をあらかじめ求めておけば、温度を変化させたときに反応速度がどれだけ変化するのかがわかります。
異なる温度\(T_1\)と\(T_2\)における反応速度定数をそれぞれ\(k_1\)、\(k_2\)とすると、\(\displaystyle \ln{(\frac{k_2}{k_1})}=\frac{E_\rm{a}}{R}(\frac{1}{T_1}-\frac{1}{T_2})\)となります。
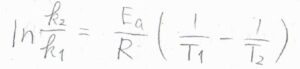
分子論的に、なぜこのような温度依存性になるのかを説明する代表的な理論である衝突理論と遷移状態理論については、こちらの記事を参照してください。


非アレニウス型の変化
ただ、この世の中のすべての変化がアレニウスの式で記述できるわけではありません。
例えば、高分子の物性を勉強した人は必ず知っていますが、主鎖セグメント緩和時間の対数は温度の逆数には比例しません。
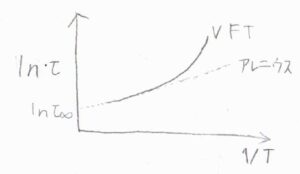
ガラス転移が起こると熱運動がほとんど停止し、セグメントの配向、ひいては応力がとても長い時間保持されるようになり、ガラス転移温度近傍で緩和時間は一気に長くなります。
この場合は、アレニウスの式ではなく、下記のVFT式でフィッティングします。

ポイントは、右辺の第二項の分母が\(T\)ではなく、\(T-T_\rm{V}\)となっていることです。
\(T_\rm{V}\)はVogel温度と呼ばれる定数で、だいたいガラス転移温度\(T_\rm{g}\)より\(50\ \rm{K}\)ほど低い温度であることが知られています。
これがあることにより、\(T\)が\(T_\rm{V}\)に近づくにつれて、アレニウスの式から外れ、発散していくような式になります。
このようにアレニウスの式に従わない場合においても、その温度における見かけ上の活性化エネルギーを計算することができます。
アレニウスの式より、見かけ上の活性化エネルギー\(E_\rm{a,app}\)は、\(\displaystyle -R\frac{\rm{d}(\ln{k})}{\rm{d}(1/\mathit{T})}\)であり、これを変形すると、\(\displaystyle \frac{RT^2}{k}\frac{\rm{d}\mathit{k}}{\rm{d}\mathit{T}}\)と書けます。

まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!