こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Boltzmann1、Boltzmann2、Boltzmann3)
それでは内容に入っていきます!
ボルツマン分布とは
それでは始めに結論の部分、ボルツマン分布について説明します。
ボルツマン分布とはある2状態の分子数の比を与えるものです。
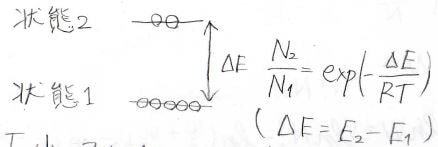
その比は絶対温度\(T\)と状態間のエネルギー差\(\Delta E\)によって変わり、温度が低いほど、またエネルギー差が大きいほど、分子は低エネルギー側に偏って分布することになります。
導出で必要な数学のテクニック
それでは実際に導出してみますが、その前に導出で必要となる数学のテクニックを紹介します。
スターリングの近似式
1つ目のテクニックはスターリング(Stirling)の近似式です。
\(n!\)の自然対数はこのような級数で表すことができ、これをスターリング展開と呼びます。
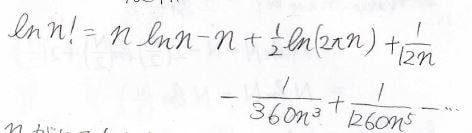
\(n\)が大きいときには高次の項を無視することができるため、仮に第二項までを取り出した場合には\(\ln{n!}\approx n\ln{n}-n\)と近似することができます。
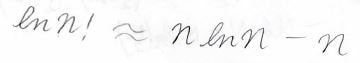
この式をスターリングの近似式と言って、統計力学では重要な式になります。
ラグランジュの未定係数法
そしてもう1つのテクニックは、ラグランジュ(Lagrange)の未定係数法です。
これはある条件に従う点の中で極値を与える変数を求めるテクニックになります。
ニ変数関数を例にすると、その条件式に当たるのが\(g(x, y)=0\)で、これを満たす点の中でさらに、\(f(x, y)\)が極値になる点を見つける方法ということです。
最初に、下に示す\(h(x, y)\)を定義します。

\(h(x, y)\)は\(f(x, y)\)から\(g(x, y)\)、すなわち\(0\)の定数\(\lambda\)倍を引いたものになります。
つまり\(h(x, y)\)と、\(g(x, y)=0\)上の\(f(x, y)\)はまったく同じ値になります。
実際に例を使った方がわかりやすいと思うので、次の例を考えてみましょう。
直線\(x+3y=2\)上の点で、\(x^2+3y^2\)が極値をとる点を考えます。
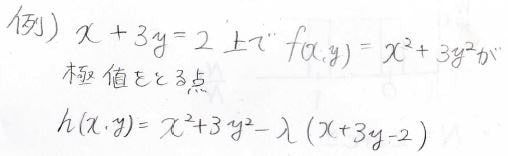
\(h(x, y)\)は\(x^2+3y^2-\lambda(x+3y-2)\)になります。
ここで\(h(x, y)\)が極値をとるときを考えると、\(x\)と\(y\)を係数\(\lambda\)で表すことができ、さらに\(x+3y=2\)から\(\lambda\)が\(1\)だとわかります。
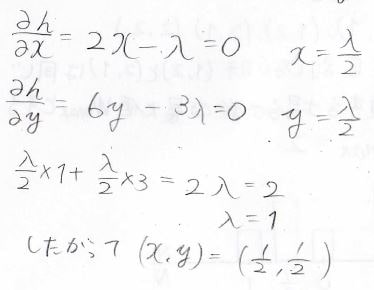
あとは\((x, y)\)に\(\lambda=1\)を代入すれば\(x^2+3y^2\)が\(\displaystyle (x, y)=(\frac{1}{2},\frac{1}{2})\)で極値をとると求めることができます。
2状態が縮退しているとき
前置きは以上で、ここからボルツマン分布の導出に入っていきます。
まず、縮退している2状態に分子がどう分布するのかを考えていきましょう。
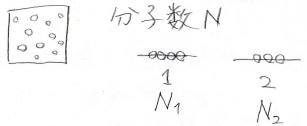
直感的に考えれば半分ずつ存在しそうですが、本当にそうなるのか実際に計算してみましょう。
全体の分子数を\(N\)として、状態\(1\)と\(2\)に存在しているそれぞれの分子数を\(N_1\)、\(N_2\)と表すことにします。
ではまず、分子が\(1\)個だけの場合を考えてみましょう。
考えられるのは状態\(1\)にあるか状態\(2\)にあるかという2通りです。
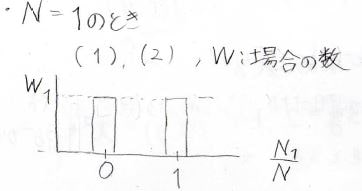
横軸を\(\displaystyle \frac{N_1}{N}\)とすると、分布は上のグラフのようになります。
分子数が\(2\)のときに考えられる状態は、この4通りになります。
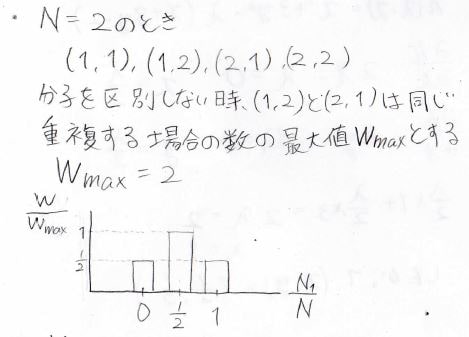
また、分子を区別しない場合には\((1, 2)\)と\((2, 1)\)は同じになるので、このように重複する場合の数を\(W\)、その最大値を\(W_{\rm{max}}\)と表すことにすると、\(N_1\)の分布は上のグラフのようになります。
分子数が\(3\)の場合も同様に考えると、高校で習う式で\(W\)を計算できます。
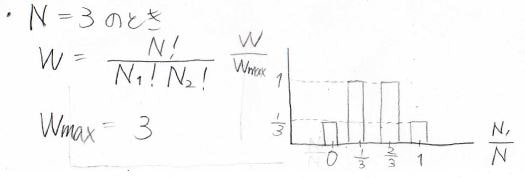
分子数がとても大きい場合についても同様に考えることができます。
ここで簡単のため、\(N_1\)と\(N_2\)を\(m\)という文字を使って書き換えます。

\(m\)は\(\displaystyle \frac{N}{2}\)からのずれの大きさを表す整数です。
ここで\(N\)を\(2\)で割っていますが、奇数で考えても結果は変わらないので、\(2\)で割り切れるものだと考えてください。
\(W\)の式は\(N=3\)のときと同様に書けるので、ここでスターリングの近似式を使うために\(W\)の自然対数をとります。

そして、\(\ln{W}\)はこのように変形されます。
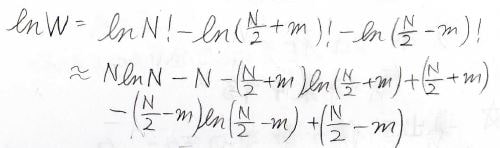
\(W_{\rm{max}}\)は分子がちょうど1:1で分かれたときなので、\(m=0\)として計算します。
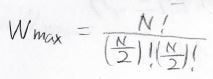
こちらも自然対数をとると、途中\(N\)と\(-N\)が相殺されて、下のように近似できます。
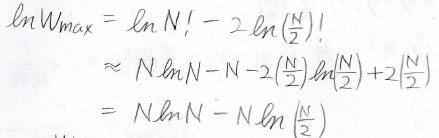
ピークの高さが\(1\)となるように\(\displaystyle \frac{W}{W_\rm{max}}\)の値を自然対数で求めると、このようになります。
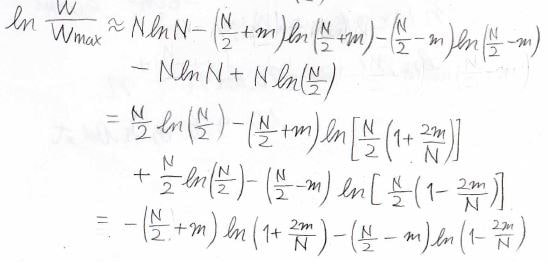
途中、第二項の真数部分を積の形で分離することにより、\(\displaystyle N\ln(\frac{N}{2})\)も相殺されるため、結果は\(\displaystyle -(\frac{N}{2}+m)\ln{(1+\frac{2m}{N})}-(\frac{N}{2}-m)\ln{(1-\frac{2m}{N}})\)となります。
そして、\(x\)がとても小さい場合には、\(\ln{(1+x)}\approx x\)と近似することができます。
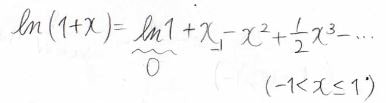
これを使うと、\(\displaystyle \ln{(\frac{W}{W_\rm{max}})}\approx \displaystyle -\frac{4m^2}{N}\)となります。

したがって、\(\displaystyle \frac{W}{W_\rm{max}}\approx \exp{(-\frac{4m^2}{N})}\)と近似されます。
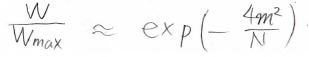
これをグラフにすると、下のように\(\displaystyle \frac{N_1}{N}=\frac{N}{2}\)を中心に左右対称な山型になります。
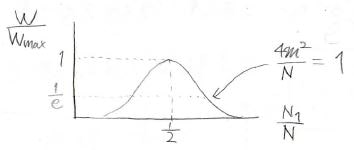
このように\(\exp{(-\alpha x^2)}\)という形の分布はガウス分布、もしくは正規分布と呼びます。
積分して\(1\)になるように規格化されたガウス関数は、下の形になります。
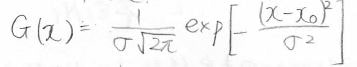
ここで\(\sigma\)は標準偏差、\(x_0\)は中央値であり、最頻値、平均値になります。
実験誤差や高分子の両末端間距離など、さまざまな場面でこの正規分布を見ることができます。
高分子の両末端間距離についてはこちらをご覧ください。

また、ここでピークの幅にも注目してみましょう。
\(\displaystyle \frac{W}{W_\rm{max}}=\rm{e}\)\(^{-1}\)のときの\(m\)は\(\displaystyle \pm\frac{\sqrt{N}}{2}\)であり、グラフ上での幅は\(\displaystyle \frac{1}{\sqrt{N}}\)になります。

いま\(N\)がとても大きい場合を考えているので、この幅はほとんど\(0\)になります。
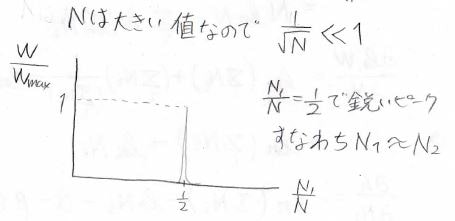
つまり、先ほどは模式的に山型のカーブを示しましたが、実際は\(\displaystyle \frac{N_1}{N}=\frac{1}{2}\)で一気に立ち上がるとてもシャープなピークになります。
したがって、縮退している2状態にはかなりの高確率で半分ずつ分子が分布することになります。
縮退していないエネルギー準位に従う分子
はい、それではいよいよエネルギー準位を考えてみましょう。
簡単のため、まずは縮退がない場合を考えます。
全体の分子数\(N\)で、離散的なエネルギー状態を考えます。

そのエネルギーは下から\(\varepsilon_0\)、\(\varepsilon_1\)と数えて、それぞれの分子数を\(N_0\)、\(N_1\)とします。
\(N_i\)をすべて足すと、全体の分子数\(N\)になり、\(\varepsilon_iN_i\)をすべて足したものが全体のエネルギー\(E\)だということになります。
ここで、ラグランジュの未定係数法を使ってみます。
分子を区別しないときに重複する場合の数\(W\)が極値をとる点を求めることで、どういう分布に落ち着くのかを調べるのが目的です。
いま、変数は無限個の\(N_i\)であり、\(N_i\)に関する条件式は\(\displaystyle \sum_i N_i=N\)と\(\displaystyle \sum_i\varepsilon_iN_i=E\)の2つがあるため、\(\ln{W}\)はこの\(h\)という関数で表すことができます。
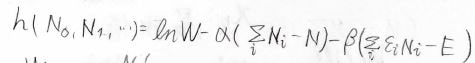
\(\ln{W}\)をある\(N_i\)について偏微分すると、\(\ln{N}-\ln{N_i}\)になるため、\(h\)を同じ\(N_i\)で偏微分したものは、こちらの形になります。
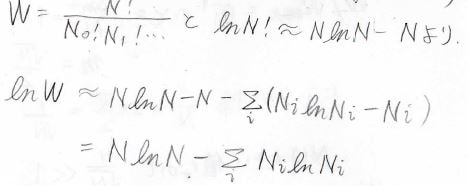
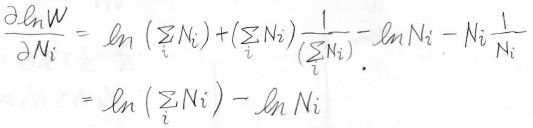

最終的に、\(\displaystyle \ln{(\frac{N_i}{N})}=-\alpha-\beta\varepsilon_i\)という式が出てきます。
これを対数でない形にして、\(\exp{(-\alpha)}\)の部分はただの定数なので\(A\)と置くと、全体の分子数\(N\)に対する\(N_i\)の占める割合は、\(A\exp{(-\beta\varepsilon_i)}\)となります。
同様に、全体の分子数\(N\)に対する状態\(j\)の分子数\(N_j\)の割合も表すことができます。
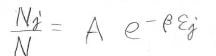
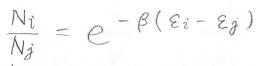
したがって、\(N_j\)に対する\(N_i\)の比は、\(A\)の部分が消えて\(\exp{[-\beta(\varepsilon_i-\varepsilon_j)]}\)となります。
縮退があるエネルギー状態をもつ分子の分布
縮退があるときには、\(N_i\)を\(\varepsilon_i\)というエネルギーをもつ全分子数とすると、縮退度\(g_i\)を使って、下のようになります。

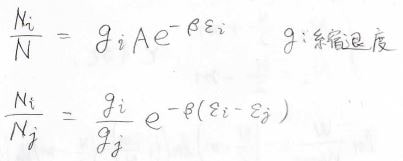
未知定数\(\beta\)の値を求める
仕上げとして、未知定数\(\beta\)の値を求めます。
考えるのは、分子がもつ全エネルギーが並進エネルギーだけである単原子理想気体分子です。
エネルギーは連続量で、\(\displaystyle \frac{1}{2}mv^2\)となります。
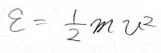
これまでの内容より、その速度分布は\(\displaystyle \exp{(-\beta \cdot \frac{1}{2}mv^2})\)に比例することになります。

全体の分子数\(N\)は、微小な速度範囲に存在する分子数\(\rm{d}\)\(N\)を足し合わせたものになり、存在確率密度\(f\)を使うと、下のように表されます。
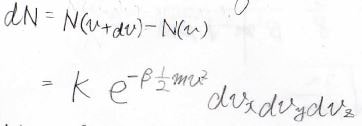
この積分を計算すると、途中極座標への変数変換とガウス積分が出てきて、最終的には\(N\)が\(\displaystyle \frac{2\pi K}{\beta m}\sqrt{\frac{2\pi}{\beta m}}\)と表せることになります。
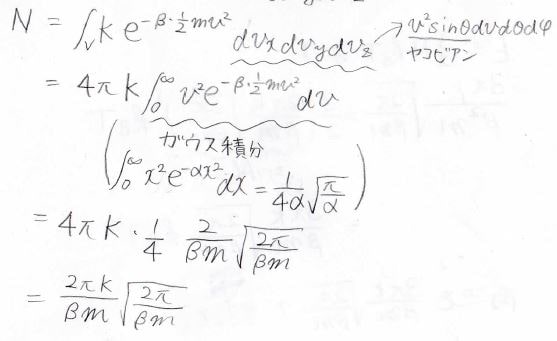
エネルギー\(E\)についても同じことをすると、\(\displaystyle E=\frac{3\pi K}{\beta^2m}\sqrt{\frac{2\pi}{\beta m}}\)となります。
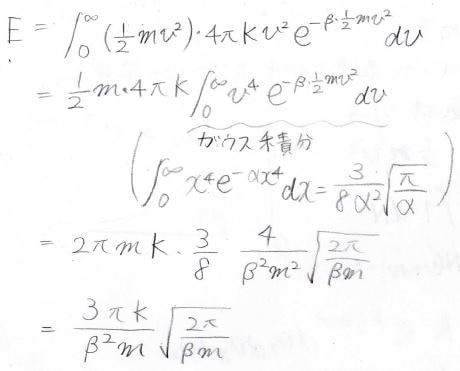
理想気体の状態方程式\(pV=nRT\)と気体分子運動論より、\(\displaystyle E=\frac{3}{2}Nk_\rm{B}\)\(T\)という関係式が別に得られるため、これに先ほど求めた\(N\)と\(E\)を入れてみます。
そして、両辺を\(\displaystyle E=\frac{3\pi K}{\beta m}\sqrt{\frac{2\pi}{\beta m}}\)で割ると、\(\beta^{-1}=k_\rm{B}\)\(T\)という式が出てきます。
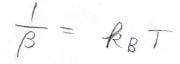
したがって、\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)となり、ボルツマン分布の式を求めることができます。
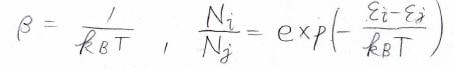
カノニカル分布
最後におまけとして、カノニカル分布というものも紹介して終わります。
全体の分子数\(N\)は各状態の分子数\(N_i\)の和となるわけですが、ここで両辺をとある状態の分子数\(N_j\)で割ります。
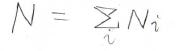
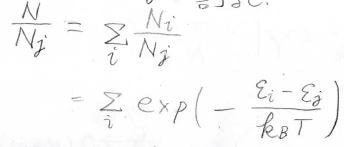
すると、右辺がボルツマン分布の無限級数となります。
\(N_j\)と\(N_i\)の比はそのままボルツマン分布で書けるため、ここから全体の分子数\(N\)に対する\(N_i\)の比を考えることができます。
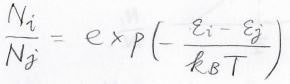
それは実際、下の形になります。
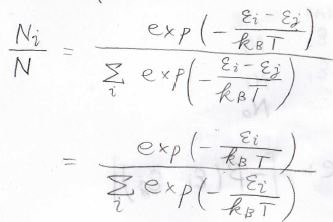
このように外界との間でエネルギーのやり取りができる閉鎖系を無数に集めた集団のうち、その状態にあるものの割合を考えたものをカノニカル分布、または正準分布と呼びます。
ここで、分母に当たる値は分配関数と呼ばれ、統計力学において、重要なパラメータになります。
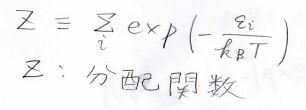
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!