こんにちは！
それでは今回も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(Gauss chain)
それでは内容に入っていきます！
酔歩鎖
まずは酔歩鎖という高分子モデルを紹介します。
酔歩というのは、英語でrandom walkと言って、つまりは酔っ払いの千鳥足のようにふらふら適当に動いていく様を指しています。
あらかじめ、100回動くとか決めておけば、そのふらふら動いた軌跡を高分子の鎖として考えることができます。
例えば二次元酔歩鎖であれば、この碁盤の目の上を上下左右に等確率で動く点を考えます。
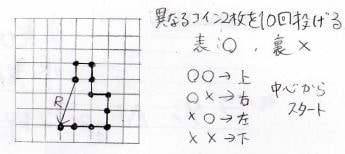
異なる2枚のコインを同時に投げてその表裏の組み合わせで点が動くものとして、ここでは仮に10回コインを投げます。
その始点と終点を結んだベクトルが両末端間ベクトル\(\boldsymbol{R}\)となります。
このコインを投げる一連の操作はやるたびに異なる結果が得られるため、両末端間距離を厳密に予測することはできません。
しかし、\(8\)とか長い距離になる確率は低いだろうなどという予想は立てられます。
つまり、この操作を無限回繰り返して\(R\)がどの範囲に収まるのか棒グラフを作るとすると、どの値をとりやすいという傾向が見えてくるということです。
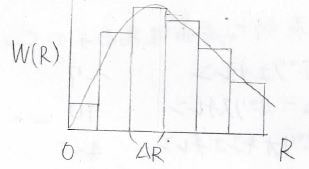
仮に棒グラフの横軸の刻み幅を無限に小さくしていくと、その分布はある連続関数になります。
例えば、自由連結鎖を仮定して\(R\)の分布を出すと、このような形になります。
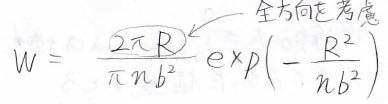
ここで、\(n\)は結合の本数、ここではコインを投げる試行回数で、\(b\)が結合長、ここでは格子点間距離です。
\(2\pi R\)は二次元の全方向を考慮した部分であり、方向を考慮しない場合は単純なガウス関数、つまり正規分布に従います。
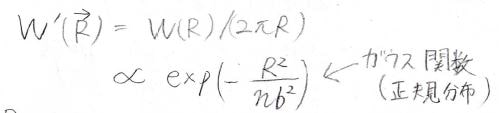
この正規分布についてはこの先、実験の誤差を議論する際にも必須の概念です。
少し後の記事でその導出をしますが、知らなかった方はぜひご自分でも調べてみてください。
そして、\(R\)の分布が正規分布に従う高分子鎖のことを、ガウス鎖と呼びます。
それでさっきは二次元でしたが、三次元でも同様に導くことができまして、このような形になります。
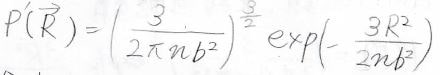
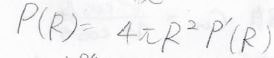
横軸を\(R\)としてこの分布関数を書きますと、こんな感じで、方向を考えない場合には\(R=0\)となる確率が最も高いですが、方向を考えた場合には原点を通り、山なりのカーブになります。
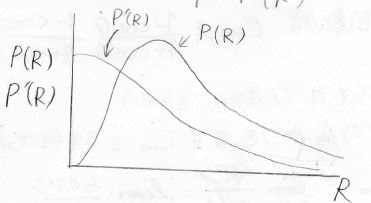
ある方向について\(R\)は小さくなりやすくても、全方向で全部\(R\)が小さくなるかと言えば、そういうわけではないということです。
平均二乗両末端間距離を計算
では、この分布関数から平均二乗両末端間距離を求めてみましょう。
分布関数に求めたい\(R^2\)をかけて期待値を出します。
途中ガウス積分が出てきますが、これを解くと結局\(R^2\)の平均は\(nb^2\)ということになり、これは自由連結鎖の答えと全く同じになります。
自由回転鎖では全方向に等確率、三次元酔歩鎖では前後左右上下の6方向に等確率という違いがありますが、\(n\)を大きくしていけば結果は同じということです。
それでは自由回転鎖と束縛回転鎖ではどうなるでしょうか？
これらについては別の記事で一度紹介していますが、おさらいしておくと、自由回転鎖は結合角が一定で内部回転角がランダム、束縛回転鎖は結合角が一定で、内部回転角の存在確率があるポテンシャルに従うとしたものです。
詳しくはこちらを参照してください。
この場合は見かけ上の結合長を変えることで自由連結鎖と同じようにガウス関数で両末端間距離の分布を記述できます。
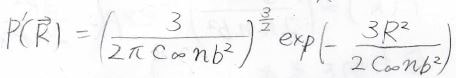
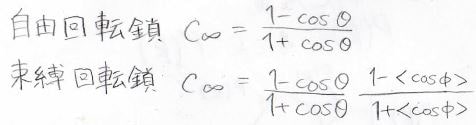
つまり、自由回転鎖と束縛回転鎖もガウス鎖モデルの1つであるということです。
ここで見かけ上の結合長にするための定数として\(C_\infty\)というものを使いましたが、この定数には名前が付いていて、特性比と言います。
自由連結鎖、あるいは酔歩鎖で予想される平均二乗両末端間距離からどれくらい広がっているのかを示します。
定義としてはこうなります。
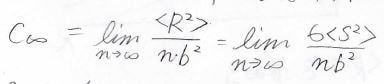
自由回転鎖や束縛回転鎖ではこの特性比が\(1\)にならないということなので、ここに結合角や内部回転ポテンシャルが反映されるということになります。
ペンタン効果
そしてこの特性比には隣接する2つの内部回転角に起因するペンタン効果というものが反映されます。
束縛回転鎖では個別の内部回転角しか考えていないので、ここからさらに分子の広がりを考えなければいけません。
ポリエチレンを例にお話しするとこの図のように2つの内部回転角\((\phi_2, \phi_3)\)が\((60^\circ, -60^\circ)\)もしくは\((-60^\circ, 60^\circ)\)のときに、4つ隣の炭素に結合した水素原子が自身に結合した水素原子とぶつかるということが起こります。
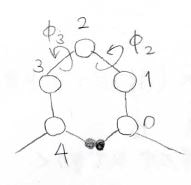
この反発を避けるように分子が広がりを持つ効果のことをペンタン効果と言います。
実際に\(\rm{n}\)\(-\)ブタンの内部回転ポテンシャルからポリエチレンの特性比を考えると\(3.7\)になるんですが、実際のポリエチレンは約\(7\)という特性比を持ちます。
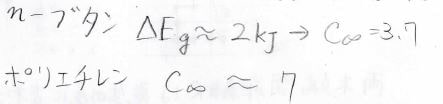
この差はペンタン効果のように複数の内部回転角の組み合わせを取りにくいという効果によるものです。
代表的な特性比の値
それでは最後、代表的な高分子について特性比を見ていって終わりましょう。
まず、ポリエチレンからポリスチレンになると側鎖が大きくなるわけですが、そうなるとペンタン効果のように反発が起こりやすくなり、特性比は大きくなります。
そして、ポリエチレンオキシドとかPEOとも呼ぶポリオキシエチレンですが、酸素原子上には側鎖がないため、ポリエチレンより小さな構造をとりやすいと予想され、実際に特性比は少し小さくなっています。
ポリブタジエンでは、よく弾むトランス-1,4-付加体の方が大きな広がりをもつということがこの表からわかります。
まとめ
はい、それでは今回の内容は以上ですので、最後軽くおさらいをやって終わります。
今回はガウス鎖と特性比についてお話ししました。
使ったのは酔歩鎖という高分子モデルで、酔っ払いの千鳥足のように格子状の点をランダムな方向へ進んでいきまして、その通った道筋が高分子だと考えます。
その両末端間距離の分布を連続関数として求めた場合には正規分布となり、このように両末端間距離が正規分布に従う高分子鎖はガウス鎖と呼ばれます。
この酔歩鎖モデルについて平均二乗両末端間距離を計算すると\(nb^2\)となり、これは自由連結鎖の値と一致します。
さらに見かけ上の結合長を大きくすることで自由回転鎖と束縛回転鎖も考えることができます。
\(nb^2\)に対して平均二乗両末端間距離の比をとったものは特性比と呼び、結合角や内部回転ポテンシャルを反映した、分子の広がりを表すパラメータになります。
そして、反映するものはそれだけではなくて、ペンタン効果をはじめとする複数の内部回転角の組み合わせで立体反発が大きくなる効果も反映しており、この効果は側鎖が大きいほど顕著になります。
今回は以上です。
どうもありがとうございました！
