こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(velocity distribution)
マクスウェル-ボルツマン分布
まず、マクスウェル-ボルツマン分布についてのおさらいをやります。
考えているのは、分子が並進エネルギー以外のエネルギーをもたない系で、分子自体の体積や相互作用もない理想気体です。
分子がもつエネルギーは一様ではなく、ボルツマン分布に従っているとして、速度ベクトルの絶対値\(v\)の分布を導くと、下の式が得られます。

これがマクスウェル-ボルツマン分布で、三次元空間で並進運動している理想気体分子の速度分布を表します。
ここで、\(R\)は気体定数(\(=8.31\ \rm{J\ K^{-1}\ mol^{-1}}\))です。
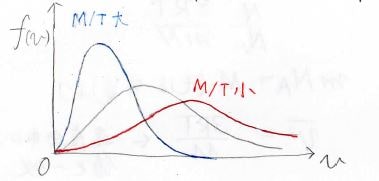
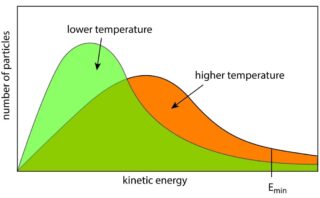
この関数は、モル質量\(M\)と絶対温度\(T\)の比によって決まり、下図の中で、温度が高いもしくはモル質量が小さい場合には赤、その逆が青のような形になります。
詳しくは、下の記事を参照してください。
最確の速さ
ここからが新しい内容です。
このマクスウェル-ボルツマン分布を使って最確、すなわち最も高い割合となる速さ\(v^\ast\)を求めます。
ちょうど\(f\)の傾きが\(0\)になる点が最確の速さになるので、\(\displaystyle f\)を\(\displaystyle v\)について微分します。
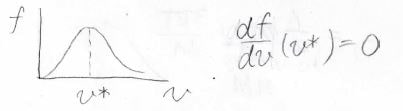
計算はこのようになり、三次方程式になります。
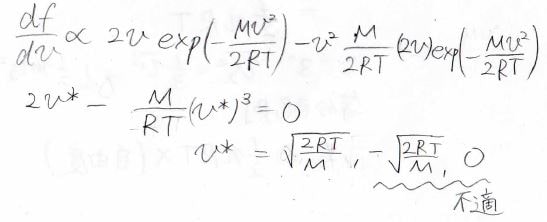
解は3つ得られますがそのうち2つは\(0\)と負の値で、不適になります。
結果、\(\displaystyle v^\ast=\sqrt{\frac{2RT}{M}}\)となります。
平均の速さ
続いて、平均の速さ\(\bar{v}\)も出してみましょう。
平均値は、期待値として計算できます。

途中、ガウス積分の公式を使って変形すると、\(\displaystyle \bar{v}=\sqrt{\frac{8RT}{\pi M}}\)となります。
速さの二乗の平均
同様にして、速さの二乗の平均も計算できます。
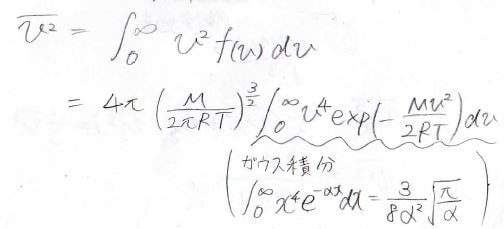
こちらも、途中にガウス積分が出てきます。

これを計算すると、\(\displaystyle \bar{v^2}=\frac{3RT}{M}\)になります。
気体分子運動論との比較
最後に、高校で習う気体分子運動論から導かれる速さの二乗の平均と比較してみましょう。
考えるのは、一辺が\(L\)の立方体の中に理想気体分子が\(N\)個入っている系です。
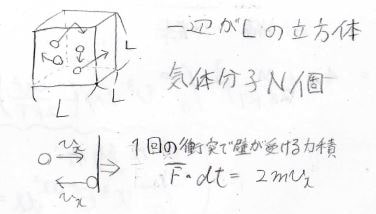
\(x\)軸に垂直な面に分子が完全弾性衝突すると、もともとの\(v_x\)から逆方向へ同じ\(v_x\)で進んでいくことになります。
ここで運動量保存則より、壁には\(2mv_x\)という力積が与えられます。
これは1回の衝突の話なので、これに壁への衝突頻度\(\displaystyle \frac{v_x}{2L}\)をかければ、単位時間あたりに1個の分子から壁へ与えられる力を求めることができます。
分子は\(N\)個あるので、これに\(N\)をかけて、それを壁の面積\(L^2\)で割ったものが圧力\(p\)になります。

ここで、\(v_x^2\)には分布があるので、平均値を使います。
分子は等方的に運動しているので、\(\bar{v_x^2}\)は\(\bar{v_y^2}\)、\(\bar{v_z^2}\)と等しくなり、速度ベクトルの絶対値\(\bar{v^2}\)の\(\displaystyle \frac{1}{3}\)倍になります。
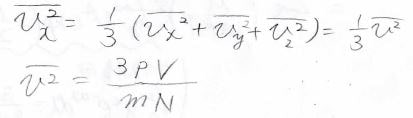
したがって、\(\displaystyle \bar{v^2}=\frac{3pV}{mN}\)と出てきます。
ここで理想気体の状態方程式\(pV=nRT\)を使うと、このように変形できます。

\(m\)は分子1個あたりの質量であり、これがアボガドロ数個だけ集まるとモル質量\(M\)となるので、結局\(\displaystyle \bar{v^2}=\frac{3RT}{M}\)となり、先ほどマクスウェル-ボルツマン分布から求めた値と一致します。

系全体のエネルギーは、気体分子運動論から\(\displaystyle \frac{3}{2}nRT\)と出てきますが、ボルツマン分布の導出過程でもこの式を使っているので、この結果は必然です。
詳しくはこちらを参照してください。

また、ここで\(\bar{v_x^2}\)は\(\bar{v^2}\)の\(\displaystyle \frac{1}{3}\)倍というように\(x\)、\(y\)、\(z\)という3つの自由度に等分配されるので、1つの自由度に関してのみ考えた場合のエネルギーは\(\displaystyle \frac{1}{2}nRT\)であり、これに自由度をかけたものが全体のエネルギーになります。
![]()

この法則を等分配則と言い、分子が並進だけでなく振動や回転の自由度をもっている場合も、同様に考えることができます。
詳しくは、こちらの記事で解説しています。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!