こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(character table)
始めに
点群の内容は、手元に分子模型があったほうが圧倒的に理解しやすいです。
5000円前後でおすすめの分子模型があったので、ここで紹介しておきます。
類
まず、類について改めて説明します。
対称操作の記事で練習問題をしたときに、\(C_\rm{3v}\)群に属するアンモニア分子について可能な対象操作は、恒等操作、2つの\(2\)回回転操作、3つの鏡映操作があると言いました。
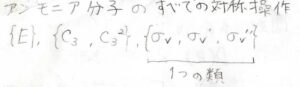
そして、回転操作と鏡映操作は、それぞれが1つの類に属します。
類の定義は、次のとおりです。
ある点群\(G\)の構成要素\(R\)と\(R’\)について、下のような相似変換ができる\(S\)も\(G\)の構成要素であるとき、\(R\)と\(R’\)は同じ類に属していることになります。
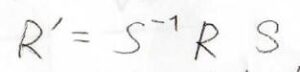
アンモニア分子を例にすると、ある鏡映面\(\sigma_\rm{v}\)面を\(120^\circ\)回転させることで、別の鏡映面\(\sigma_\rm{v}’\)面と重なります。
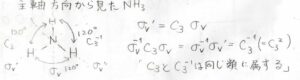
つまり、\(\sigma_\rm{v}’\)=\(C_3\) \(\sigma_\rm{v}\)という関係が成り立ちます。
これを利用すると、\(\sigma_\rm{v}\)\(^{-1}C_3 \sigma_\rm{v}\)\(=\sigma_\rm{v}\)\(^{-1} \sigma_\rm{v}’\)となって、これは\(C_3^{-1}\)に相当します。
したがって、\(C_3^{-1}=\sigma_\rm{v}\)\(^{-1} C_3 \sigma_\rm{v}\)という相似変換が可能であることから、\(C_3\)と\(C_3^{-1}\)が同じ類に属していると言えます。
対称操作の名前が同じでも、同じ類に属するとは限らなくて、例えば、水分子が属する\(C_\rm{2v}\)群がもつ2つの鏡映操作は異なる類に分けられます。
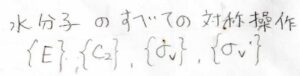
2つの鏡映面は直交していますが、水分子が\(4\)回回転操作を対称操作にもたないためです。
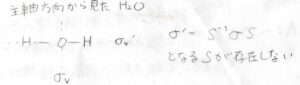
対称操作の行列表現と簡約
類の話は以上で、次に対称操作の行列表現について考えてみましょう。
ここでは、\(C_\rm{2v}\)群に属する\(\displaystyle \rm{SO}_2\)分子を例にお話していきます。
\(C_\rm{2v}\)群がもつ対称操作は、恒等操作、\(2\)回回転操作、そして、2つの鏡映操作です。
ここでは、3つの原子を通る鏡映面を\(\sigma_\rm{v}’\)面とします。

そして、\(\sigma_\rm{v}\)\(‘\)面に垂直な方向に向いた\(\rm{p}\)軌道について、対象操作の行列表現を考えていきます。
硫黄原子の\(\rm{p}\)軌道を\(p_\rm{S}\)、2つの酸素原子の\(\rm{p}\)軌道を\(p_\rm{A}\)、\(p_\rm{B}\)としておきます。
まず恒等操作は、変換前と変換後で変化はないので、単位行列として表現できます。

これと同様に\(C_2\)、\(\sigma_v\)、\(\sigma_\rm{v}’\)は、それぞれ下のような行列表現になります。

これらは共通して\((1, 2)\)成分、\((1, 3)\)成分、\((2, 1)\)成分、\((3, 1)\)成分が\(0\)になっているので、ブロック対角行列とみなせます。
そこで、まず\((1, 1)\)成分だけ取り出してみると、恒等操作で\(1\)、\(2\)回回転操作で\(-1\)、鏡映操作\(\sigma_\rm{v}\)で\(1\)、\(\sigma_\rm{v}’\)で\(-1\)となります。

ここで\(-1\)は、軌道\(p_\rm{S}\)の位相が反転することを指しています。
\(1\)は、位相に変化がないという意味です。
ここでは、これらの値を一次正方行列とみなして、\(\Gamma^{(1)}\)と表すことにします。
そして、元の三次正方行列から\(1\)行目と\(1\)列目を除いた余因子行列である二次正方行列を\(\Gamma^{(2)}\)と表すことにします。
このとき、元の三次元行列表現\(\Gamma^{(3)}=\Gamma^{(1)}+\Gamma^{(2)}\)と表記し、\(\Gamma^{(3)}\)は、\(p_\rm{S}\)が張る一次元表現\(\Gamma^{(1)}\)と\((p_\rm{A}\)\(, p_\rm{B}\)\()\)が張る二次元表現\(\Gamma^{(2)}\)の直和に簡約されたという言い方をします。
ここで、\(\Gamma^{(1)}\)に対する\(p_\rm{S}\)、\(\Gamma^{(2)}\)に対する\((p_\rm{A}\)\(, p_\rm{B}\)\()\)のことを基底と呼びます。
また一次正方行列表現は、これより小さなブロックで対角行列にできないため、これ以上簡約できない表現だと言えます。
まだ簡約できることを可約であるといい、可約でない行列表現のことを既約表現(irrep)と言います。
そして、\(\Gamma^{(2)}\)は可約であり、\(p_\rm{A}\)と\(p_\rm{B}\)の線形結合\(p_\rm{A}\)\(+p_\rm{B}\)と\(p_\rm{A}\)\(-p_\rm{B}\)を基底にすることで、対角行列にできます。
ここでは、それぞれの基底を\(p_1\)、\(p_2\)と表すことにします。
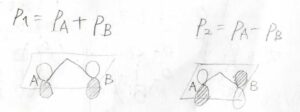
まず、\(p_1\)と\(p_2\)に\(2\)回回転操作を考えてみましょう。
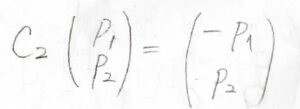
すると、\(p_1\)は位相が反転して\(-p_1\)に、\(p_2\)は位相がそのままなので、\(p_2\)に変換されます。
したがって、\(C_2\)は(1,1)成分が\(-1\)、(2,2)成分が\(1\)の対角行列となります。
同様のことを考えると、2つの鏡映操作もそれぞれ下のように表すことができます。
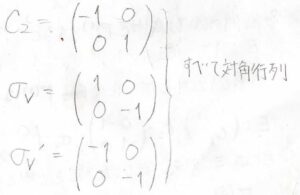
これら対角行列の\((1,1)\)成分を\(\Gamma^{(1)’}\)、\((2,2)\)成分を\(\Gamma^{(1)”}\)とすると、元の三次元行列表現\(\Gamma^{(3)}\)は\(\Gamma^{(1)}+\Gamma^{(1)’}+\Gamma^{(1)”}\)と表すことができました。
これらはすべて一次元なので既約表現であり、これ以上簡約できません。
指標
ここで、指標という言葉を紹介します。
指標とは、対称操作の行列表現について、その対角和のことを指します。
一次元表現については、その値がそのまま指標となります。
簡約する前と後で指標には変化がないという性質があり、対称操作を\(R\)、元の行列表現を\(\mathit{\bf{D}}(R)\)、指標を\(\chi (R)\)とすると、このような表が書けます。
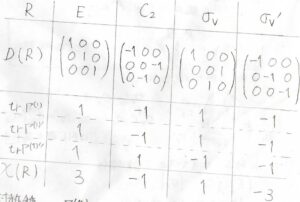
恒等操作なら\(1+1+1=3\)、\(2\)回回転操作なら\(-1-1+1=-1\)といったように、元の三次元表現の対角和は、3つの既約表現の指標の和に等しくなります。
対称種
さらに、対称種というものを考えていきます。
\(\Gamma\)は一般的な行列表現の文字として使われますが、特に群論を化学に応用したときには、アルファベットでラベルすることがあります。
このラベルのことを対称種と言います。
その表現の次元により\(\rm{A}\)や\(\rm{B}\)、\(\rm{E}\)、\(\rm{T}\)といった文字を使います。

\(\rm{E}\)は二次元表現、\(\rm{T}\)は三次元表現を指します。
\(\rm{A}\)と\(\rm{B}\)はどちらも一次元で、主軸周りの回転操作により軌道の位相が変化しないものを\(\rm{A}\)、反転するものを\(\rm{B}\)とします。
また、その中でも\(\sigma_\rm{v}’\)面について鏡映操作をしたときに位相に変化がないものには\(1\)、反転するものには\(2\)という添字をつけることにします。
例えば、先ほど求めた既約表現のうち、\(\Gamma^{(1)”}\)の基底である\(p_2\)は、回転により位相は変化しないですが、鏡映により位相が反転するので、\(\rm{A}_2\)の対称種でラベルされます。
\(Gamma^{(1)}\)の基底である\(p_\rm{S}\)と\(\Gamma^{(1)’}\)の基底である\(p_1\)はどちらも回転によって位相が反転しますが、鏡映では位相に変化がないので、\(\rm{B}_1\)となります。
そしてここまでは、\(\sigma_\rm{v}\)面に対して垂直な方向へ向いた\(\rm{p}\)軌道に関してのみ考えてきましたが、ほかの\(\rm{p}\)軌道や\(\rm{s}\)軌道について考えると、\(\rm{A}_1\)や\(\rm{B}_2\)でラベルされる既約表現の基底も見つけることができます。
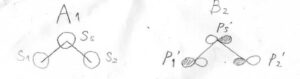
以上より、\(C_\rm{2v}\)群には、\(\rm{A}_1\)、\(\rm{A}_2\)、\(\rm{B}_1\)、\(\rm{B}_2\)という4種類の対称種があることになります。
指標表
それぞれの指標をまとめると、このような表が書けて、この表のことを指標表と言います。

まず、左上に群の名前がSchoenflies系とHermann-Mauguin系の2通りで書かれています。
それから、対称種のアルファベットを左の列、対称操作を上の行に書き、それぞれの対称種、対称操作に対応する指標も書きます。
見方としては、例えば、\(\rm{A}_1\)は回転操作、鏡映操作によって位相が反転しないため、すべての対象操作について指標が\(1\)になります。
\(\rm{B}_2\)については回転操作と\(\sigma_\rm{v}\)面についての鏡映操作で位相が反転するので、そこの指標が\(-1\)になるといった具合です。
右上にある\(h\)は対称操作の個数のことで、位数と呼びます。
群論の定理として、対称操作の類の数は対称種の数に等しく、位数はすべての対称種の指標の\(2\)乗の和に等しなるくので、対称操作がわかればすべての対称種もわかります。
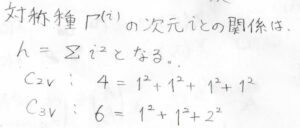
例えば\(C_\rm{2v}\)群は、類が4つ、位数が\(4\)ですが、\(4=1^2+1^2+1^2+1^2\)となるため、一次元の対称種を4つもつことがわかります。
\(C_\rm{3v}\)群であれば、類が3つ、位数が\(6\)ですが、\(6=1^2+1^2+2^2\)となるため、一次元の対称種を2つと二次元の対称種を1つもつということになります。
そして、指標表を見ると、位数の下に\(x\)や\(xy\)、\(R_x\)などの文字が書いてあります。
\(x\), \(y\), \(z\)
まず、\(x\)、\(y\)、\(z\)は既約表現の座標と言います。
ここでは、中心原子を原点として、主軸を\(z\)軸、\(\sigma_v\)面に平行な軸を\(x\)軸、\(\sigma_\rm{v}\)\(‘\)面に平行な軸を\(y\)軸と考えるという意味です。
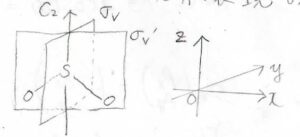
そうすると、中心原子の\(\rm{p}\)軌道がどの対称種の基底となるのかというのも、この表からわかります。
例えば、硫黄原子の\(\rm{p}\)\(_z\)軌道はあらゆる対称操作によっても、位相に変化がないため、\(\rm{A}_1\)の既約表現の基底になります。
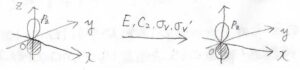
\(R_x\), \(R_y\), \(R_z\)
そして、\(R_x\)、\(R_y\)、\(R_z\)は軸まわりの回転を指します。
例えば、\(R_z\)は\(z\)軸まわりの回転を指しますが、\(\sigma_\rm{v}\)面、\(\sigma_\rm{v}’\)面について鏡映をとると、回転の方向が逆回りになります。
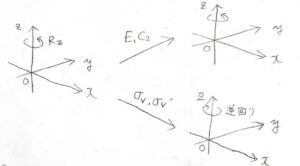
これが、\(-1\)という指標に対応するので、\(R_z\)は\(\rm{A}_2\)の対称性をもつことになります。
\(x^2\), \(xy\)など
そして、\(x^2\)や\(xy\)などは、対称種の座標の二次の項と言われます。
中心原子の\(\rm{d}\)軌道がどの既約表現の基底となるのかというのが、ここからわかります。
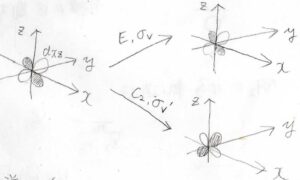
例えば、\(\rm{d}\)\(_{xz}\)軌道は、\(2\)回回転操作と\(\sigma_\rm{v}’\)面についての鏡映操作で位相が反転するので、\(\rm{B}_1\)の対称性をもつことになります。
指標と縮退度の関係
恒等操作の指標は、その表現の次元を表しますが、これは基底の個数とも等しいため、その対称性をもつ軌道の縮退度に等しくなります。
つまり、一次元表現である\(\rm{A}\)や\(\rm{B}\)の対称性をもつ軌道には、縮退がありません。
そして、\(\rm{E}\)の対称性では縮退度が\(2\)、\(\rm{T}\)では\(3\)になります。
例えば、アンモニア分子の水素原子3つについて、分子軌道の図を考えましょう。
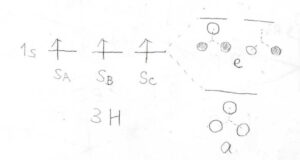
すると、まず3つの\(1\rm{s}\)軌道のすべてが同じ位相となったものは\(\rm{A}_1\)の対称性を持っています。
ここでは、\(\rm{A}_1\)の対称性をもった波動関数を、\(a_1\)と表すことにします。
そして、すべての位相が同じにならない場合は、それ単独で\(3\)回回転操作を表現できるような波動関数はないので、線形独立な2つの波動関数の組が二次元表現\(\rm{E}\)の基底となります。
これも\(e\)と表すことにします。
また、窒素原子については\(2\rm{s}\)軌道と、\(2\rm{p}\)\(_z\)軌道が\(\rm{A}_1\)の対称性をもちます。
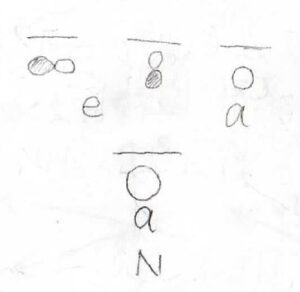
残った2つの\(\rm{p}\)軌道のそれぞれでは一次元表現の基底とはならないので、エネルギー的に等価な軌道の対として、\(\rm{E}\)の対称性をもちます。
最終的にこれらの軌道は、同じ対称性をもつ者同士で、結合性軌道と反結合性軌道を作ります。
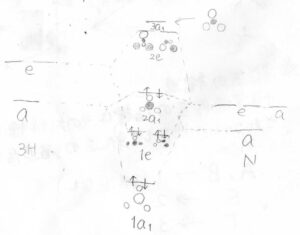
その結果、上のようなアンモニアの分子軌道ダイアグラムが書けて、恒等操作の指標と縮退度が等しくなることが確認できます。
共有結合の形成と対称性の関係については、こちらの記事を参照してください。

※アンモニアの分子軌道ダイアグラムが手元になかったため、エネルギーの大小関係は、お手元にある参考書等で確認してください。
練習問題
それでは最後、練習問題をやって終わります。
(1)\(C_\rm{3v}\)群の指標表で、回転操作と鏡映操作の指標が抜けているので、それを埋めてください。
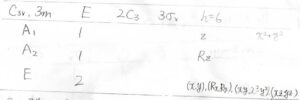
(2)\(C_\rm{3v}\)群に属する架空の分子\(\displaystyle \rm{AB}_3\)があったときに、中心原子\(\displaystyle \rm{A}\)の\(\rm{d}\)軌道のうち、縮退する分子軌道に寄与しないものをすべて答えてください。
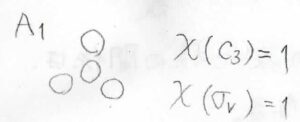
これは、回転操作、鏡映操作いずれにしても、位相の反転は起こらないので、どちらの指標も\(1\)になります。
そして、\(\rm{A}_1\)ではない一次元表現の基底としては、下のような分子軌道の形が挙げられます。
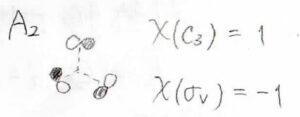
回転操作では位相はそのままで、鏡映操作では位相が反転するので、それぞれの指標は\(1\)と\(-1\)になります。
そして、対称種\(\rm{E}\)の指標がいちばん難しいと思いますが、中心原子の\(\rm{p}\)\(_x\)軌道と\(\rm{p}\)\(_y\)軌道が基底になるので、これについて行列表現を考えましょう。
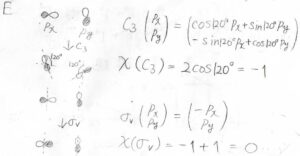
まず、\(xy\)平面上で\(\rm{p}\)\(_x\)軌道を反時計まわりに\(120^\circ\)回転させると、その\(x\)成分は\(\rm{p}\)\(_x\)軌道の\(\cos{120^\circ}\)倍となります。
そして\(y\)成分が\(\rm{p}\)\(_y\)軌道の\(\sin{120^\circ}\)倍です。
\(\rm{p}\)\(_y\)軌道の回転も同様に考えると、結局\(C_3\)の行列表現は、\(\displaystyle \begin{pmatrix}\cos{120^\circ}&\sin{120^\circ}\\-\sin{120^\circ}&\cos{120^\circ}\end{pmatrix}\)だとわかります。
指標はその対角和であるため、\(2\cos{120^\circ}=-1\)となります。
反転についてはもっと簡単で、\(\sigma_\rm{v}\)の行列表現は\(\displaystyle \begin{pmatrix}-1&0\\0&1\end{pmatrix}\)となります。
したがって、鏡映操作の指標は\(-1+1=0\)となります。
続いて(2)は、指標表の一番右にある座標の二次の項に着目します。
そこには、対称種\(\rm{E}\)の基底となる組み合わせが書いてあって、これらは分子軌道に寄与しても縮退した軌道を作ることになります。
ここには、\((xy,x^2-y^2)\)、そして\((xz,yz)\)とあるので、これらの添え字が付いた\(\rm{d}\)軌道は縮退した分子軌道に寄与することになります。
残った\(\rm{d}\)\(_{z^2}\)軌道だけが、一次元対称種\(\rm{A}_1\)の基底となるため、縮退した分子軌道に寄与しないことになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!






