こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(classification of phase transition)
相転移に伴う化学ポテンシャルの変化
まず、混合物も含む一般的な系について、成分\(i\)の化学ポテンシャル\(\mu_i\)は、こちらの式で定義されます。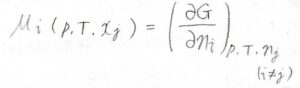
ここで\(p\)は圧力、\(T\)は温度、\(G\)は全体のギブズエネルギー、\(n\)は物質量、\(x\)はモル分率、\(j\)は成分\(i\)以外のすべての成分を指します。
単成分系については、ギブズエネルギーが物質量に比例するので、化学ポテンシャルはモルギブズエネルギーと等しくなります。
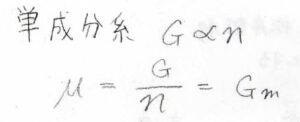
そして、熱力学基本式より、ギブズエネルギーの全微分\(\rm{d}\)\(G=-S\rm{d}\)\(T+V\rm{d}\)\(p\)となるので、化学ポテンシャルの全微分\(\rm{d}\)\(\mu\)は、\(S_\rm{m}\)\(\rm{d}\)\(T+V_\rm{m}\)\(\rm{d}\)\(p\)となります。
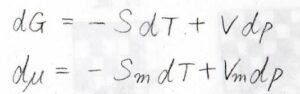
ここで、\(S\)はエントロピー、\(V\)は体積、\(S_\rm{m}\)はモルエントロピー、\(V_\rm{m}\)はモル体積です。
ここで仮に、\(\alpha\)相から\(\beta\)相への転移が起こったとして、\(T\)についての\(\mu\)の偏導関数を考えます。
すると、偏導関数は転移の前後でモルエントロピーの差分だけ変化することになります。
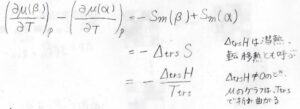
いま、この差分を転移エントロピー\(\Delta_\rm{trs}\)\( S\)と呼びます。
また、この値は転移エンタルピー\(\Delta_\rm{trs}\)\( H\)を使うと、\(\displaystyle \frac{\Delta_\rm{trs}\mathit{H}}{T}\)とも書けます。
\(\Delta_\rm{trs}\)\( H\)は潜熱、もしくは転移熱とも呼びます。
状態変化では、転移エンタルピーは\(0\)ではないため、この偏導関数は転移温度\(T_\rm{trs}\)で不連続になります。
このとき、微分する前の化学ポテンシャルは、転移温度で傾きが変わることになります。
同様に、圧力について偏微分すると、モル体積の差分だけ偏導関数が変化します。
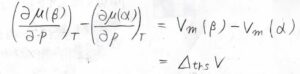
ここから相転移を分類していきます。
エーレンフェストの分類
これから話す分類は、エーレンフェストの分類と呼ばれているものです。
1次相転移
まず1次相転移というのは、\(\displaystyle (\frac{\partial \mu}{\partial T})_p\)が不連続な関数になるものです。
言い換えると、\(\Delta_\rm{trs}\)\( H\)が\(0\)ではない転移が1次相転移に分類されます。
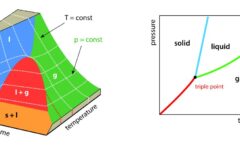
先述のとおり、固相、液相、気相といった状態の変化が1次相転移の最も簡単な例です。
圧力を一定として、温度に対して、それぞれの状態関数をグラフにすると、下のようになります。
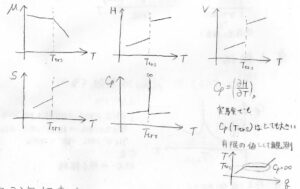
まず、化学ポテンシャル\(\mu\)は転移温度で傾きが変化して、折れ曲がります。
エンタルピー\(H\)は転移温度でジャンプします。
同時にモル体積も変化するので、体積\(V\)もジャンプします。
エンタルピーが不連続であることから、エントロピー\(S\)も不連続になります。
ここでは、数学的に微分できない関数について、形式上、微分ができるものだと考えていることに注意してください。
そして本来、不連続な関数も微分できないわけですが、形式上、偏導関数が発散するものと考えることにします。
すると、定圧熱容量\(C_p\)は転移温度で無限大となる関数になります。
実際の測定でも、転移温度における\(C_p\)はとても大きな有限の値として観測されます。
横軸に与えた熱量\(q\)、縦軸に温度\(T\)をとると、画像右下のグラフになります。
2相が共存しているときには、どれだけ熱を与えても温度が変化しないので、熱容量はとても大きいことになります。
2次相転移
次に2次相転移というものを紹介します。
これは、\(\displaystyle (\frac{\partial \mu}{\partial T})_p\)は連続ですが、もう一度温度について偏微分すると不連続になるような相転移を指します。
ここでは\(\Delta_\rm{trs}\)\( H=0\)になります。
例えば、物質を冷却していったときの常伝導-超伝導転移がこれにあたります。
そのとき、圧力一定での状態関数の温度依存性は、このようになります。
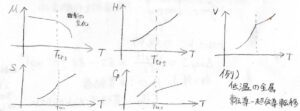
化学ポテンシャル\(\mu\)は、転移温度で曲率が変化します。
エンタルピー、体積、エントロピーは転移温度で傾きが変化します。
そして、定圧熱容量\(C_p\)は不連続となります。
そして、この考え方を広げると、さらに高次の相転移も考えることができます。
しかし実験的には、不連続なのか単なる誤差なのか判定が難しいため、単に高次相転移とだけ呼ぶことも多いです。
擬2次相転移
前回の記事で、ガラス転移は相転移とはまったく異なる現象であることを説明したのですが、熱の流速を見る限りは2次相転移に似た挙動を示します。
詳しくはこちらの記事をご覧ください。
そのため、ガラス転移のことを擬2次相転移と言うことがあります。
熱分析の装置としては、示差走査熱量計、略してDSCというものがメジャーです。
測定原理については、また高分子の話のときにお話ししたいと思いますが、簡単に言うと、温度変化の速度を制御したときの、熱の出入りを観察しています。
横軸に温度、縦軸に熱の流速をプロットすると、例えばこんなグラフが得られます。
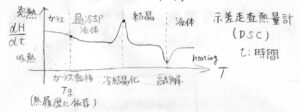
いま、昇温速度を一定としているため、温度変化は測定時間に比例します。
そのため、熱力学的な現象については、縦軸を熱容量としても同じ形のグラフになります。
例えば、融解が起こったときには、熱が一気に吸収されるため、熱容量はグラフ上で大きな谷の形として現れます。
それに対して、ガラス転移は、ベースラインの変化として観測されるため、2次相転移のように見えます。
2次相転移との違いは、ガラス転移はあくまで速度論的な現象であるため、温度変化速度によって、どの温度で起こるのかが変わってしまうことです。
また、この測定の前に、何度でどれくらいの時間冷却していたかということにも影響されます。
このような情報のことは、まとめて熱履歴と呼びます。
もちろん、熱力学量は現在のパラメータだけあれば値が決まるため熱履歴に依存せず、どんな温度変化速度でも決まった温度で融解や蒸発が観測されます。
\(\lambda\)転移
そして、\(n\)次相転移以外にも、エーレンフェストが分類した相転移があります。
\(\lambda\)転移は、\(\displaystyle (\frac{\partial \mu}{\partial T})_p\)が連続かつ熱容量が発散するような転移を言います。
例えば、ヘリウムの常流動-超流動転移や合金の秩序-無秩序転移がこれにあたります。
熱容量は温度の上昇とともに増大していき、転移温度で発散します。

このグラフの形が、ギリシャ文字の\(\lambda\)に似ているため、\(\lambda\)転移と呼ばれています。
そして、\(\lambda\)転移が起こる温度のことは、\(\lambda\)点と言います。
分子論的解釈
最後に、これらの相転移がどのような分子論的起源で起こっているのかを考えて終わりにします。
1次相転移
まずは、蒸発を例に1次相転移について考えます。
蒸発する前後では、分子間距離が大きく変化します。

すると、同時に分子間相互作用も小さくなります。
これが転移温度で急に起こるため、エンタルピーのジャンプが起こるというわけです。
ちなみに、蒸発に伴うモルあたりのエントロピー変化は、多くの物質で\(85\sim 88\ \rm{J\ K}\)\(^{-1} \rm{mol}\)\(^{-1}\)となることが知られています。
この経験則は、トル―トンの規則と呼ばれています。
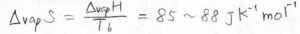
これは、液体から気体になるときの相互作用の変化は、多くの物質で同じくらいになるということを言っています。
ただし、\(\displaystyle \rm{H_2O}\)など水素結合がある場合は例外で、液体がとても安定となるため、蒸発エントロピーは大きな値になります。
また、\(\displaystyle \rm{CH_4}\)など慣性モーメントが小さい場合は、蒸発エントロピーが小さくなります。
回転のエネルギー準位は慣性モーメントの大きさに反比例するので、慣性モーメントが小さいときには、準位間のエネルギー差が大きくなります。

すると、ボルツマン分布より、低エネルギー側に分子が集中して分布することになるため、気体のエントロピーは小さくなり、液体との差も小さくなります。
2次相転移
2次相転移の例として、ここでは固相から固相への転移を考えます。
転移の前後で、結晶構造が正方晶から立方晶に変化したとします。
直方体が転移温度で立方体になることを考えると、このように長辺方向への熱膨張率がほかの2方向に比べて小さければよいことになります。

温度上昇によって連続的に立方晶に近づいていくため、エンタルピーはジャンプしません。
3辺の長さが等しくなったタイミングで、方向の区別がなくなり、それ以降は3方向に同じだけ熱膨張するようになります。
\(\lambda\)転移
\(\lambda\)転移は合金の秩序-無秩序転移を例にお話しします。
ここでは、銅と亜鉛がほぼ1:1で混ざった\(\beta\)-黄銅を考えます。
格子モデルを使っていきますが、図の中で塗りつぶしていないものを銅、塗りつぶしているものを亜鉛だと思ってください。
まず、絶対零度近傍では、下図のように、銅と亜鉛の原子が交互に並んだ配列になります。

ここから温度を上げていくと、ある温度で、このように局所的な原子の入れ替えが起こります。
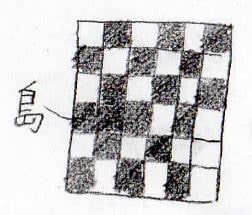
入れ替えによってできた、同種の原子が隣り合った領域のことは、島と呼びます。
さらに熱を加えていくと、あらゆるところで入れ替えが起こり、このように無秩序な配列になります。

この変化は、共同現象性という性質をもっています。
これは、ある1か所で起こった変化によって、その周りが変化しやすくなり、全体に波及していくという性質です。
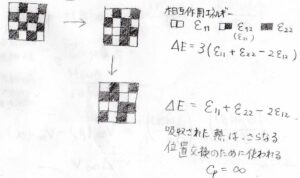
例えば、規則正しい配列から1か所で入れ替えが起こったとき、エンタルピー変化は\(3(\varepsilon_{11}+\varepsilon_{22}-2\varepsilon_{12})\)となります。
ここで、\(\varepsilon_{11}\)は銅原子どうし、\(\varepsilon_{22}\)は亜鉛原子どうし、\(\varepsilon_{12}\)は銅原子と亜鉛原子間の相互作用エネルギーです。
1個の原子について、相互作用する原子が4つであるこの格子モデルでは、\(3\)が付きます。
そして、さらにその1つ上にある原子どうしが入れ替わったときも考えます。
すると、エンタルピーの変化は\(\varepsilon_{11}+\varepsilon_{22}-2\varepsilon_{12}\)となります。
さきほどの\(\displaystyle \frac{1}{3}\)倍のエネルギーで、入れ替えが起こることになります。
このように、入れ替わった場所の近くでは、さらに変化が起こりやすくなるため、熱がどんどん位置交換に使われやすくなり、熱運動には使われなくなります。
したがって、\(\lambda\)点付近では、熱容量が発散するということです。
しかし、この変化は連続的に起こるため、エンタルピーは連続関数となります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!