こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(contribution to mean energy and entropy)
※シートの前半は、前回の記事の内容です。

それでは内容に入っていきます!
エントロピーと分子分配関数の関係
まず、相互作用がない系において、エントロピーと分子分配関数の関係を考えます。
正準アンサンブルにおいて、カノニカル分布とボルツマンの式を利用すると、集合分配関数とエントロピーの関係を導くことができます。
詳しくは、こちらの記事を参照してください。

ここでは、結果だけを示しますが、残余エントロピーがない系について、絶対温度\(T\)におけるエントロピー\(S(T)\)と集合分配関数\(Q\)の関係は、\(\displaystyle S(T)=\frac{U(T)-U(0)}{T}+k_\rm{B}\)\(\ln{Q}\)と書けます。
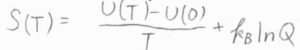
ここで、\(U\)は内部エネルギー、\(k_\rm{B}\)はボルツマン定数です。
特に、分子間相互作用がなく、互いに区別できない場合には、\(\displaystyle Q=\frac{q^N}{N!}\)となるので、これをエントロピーの式に代入すれば、エントロピー\(S(T)\)と分子分配関数\(q\)の関係が得られることになります。

ここで、\(N\)は分子数を指します。
非常に大きな整数の階乗は、スターリングの近似式を使って、階乗を外すことにします。

すると、\(\displaystyle S(T)=\frac{U(T)-U(0)}{T}+k_\rm{B}\)\((N\ln{q}-N\ln{N}+N)\)と近似できます。
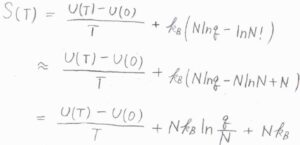
これを展開すると、\(S(T)=\frac{U(T)-U(0)}{T}+Nk_\rm{B}\)\(\displaystyle \ln{(\frac{q}{N})}+Nk_\rm{B}\)となります。
これが、分子間相互作用がなく、互いに区別できない分子の集団についてのエントロピーと分子分配関数の関係です。
\(Nk_\rm{B}\)は、物質量\(n\)と気体定数\(R\)を使えば、\(nR\)と書き換えることもできます。
ここからは、この関係を利用して、エントロピーがどのように並進や回転、振動の自由度に割り当てられるのかを考えていきます。
並進運動による寄与
始めに、並進運動の寄与を考えます。
ここでは、分子間相互作用がなく、さらに回転や振動を考えなくてもよい単原子理想気体を例に考えます。
絶対零度近傍を除き、\(\displaystyle U(T)-U(0)=\frac{3}{2}nRT\)となることから、エントロピーの式の第一項は、\(\displaystyle \frac{3}{2}nR\)と書けます。
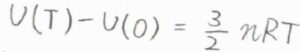
また、三次元の箱に閉じ込められた分子について、並進分配関数\(q^\rm{T}\)は、\(\displaystyle \frac{V}{\Lambda^3}\)で与えられます。
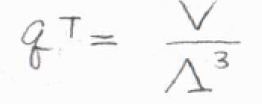
ここで、\(V\)は体積、\(\Lambda\)は熱波長(もしくは熱的ド・ブロイ波長)です。
分配関数導出の過程は、こちらの記事を参照してください。

これを代入すると、エントロピー\(S(T)\)は、\(\displaystyle nR\ln{(\frac{V_\rm{m}e^{5/2}}{N_\rm{A}\Lambda^3})}\)となります。
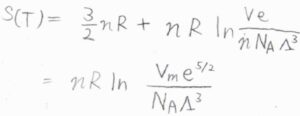
ここで、\(V_\rm{m}\)はモル体積、\(N_\rm{A}\)はアボガドロ数です。
この式は、サッカー-テトロードの式と呼ばれています。
この式の両辺を物質量\(n\)で割れば、モルエントロピー\(S_\rm{m}\)\(\displaystyle =R\ln{(\frac{V_\rm{m}e^{5/2}}{N_\rm{A}\Lambda^3})}\)という形にすることもできます。

温度が高いほど、もしくは分子が重いほど熱波長は小さく、エントロピーは大きくなります。
これは、並進運動のエネルギー準位の間隔がより小さいことで、より多数の状態が熱的に励起可能となったためであると解釈できます。
また、同じ分子数でも、大きな容器に入れたほうがモル体積が大きくなり、エントロピーも大きくなります。
回転運動による寄与
続いて、回転運動による寄与を求めます。
ここでは、自由度が\(2\)の直線型回転子について、考えていきます。
まず、等分配則より、分子が自由に回転できるほど十分に高い温度で、\(U(T)-U(0)=nRT\)です。
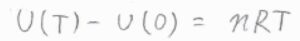
絶対温度\(T\)が回転特性温度\(\theta^\rm{R}\)よりも十分大きいとき、回転分配関数\(q^\rm{R}\)が\(\displaystyle \frac{T}{\sigma \theta^\rm{R}}\)と書けることを利用すると、モルエントロピー\(S_\rm{m}\)は、\(\displaystyle R+R\ln{(\frac{k_\rm{B}\mathit{T}}{\sigma hc\tilde{B}})}\)と書けます。
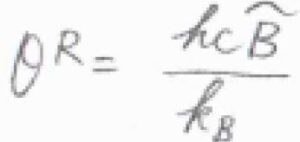
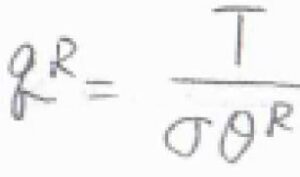
ここで、\(\sigma\)は対称数、\(h\)はプランク定数、\(c\)は光の速さ、\(\tilde{B}\)は回転定数です。
大きく、重い分子ほど慣性モーメントは大きく、回転定数は小さくなるため、エントロピーは大きくなります。
ただし、あくまでこの式は、高音域における分子分配関数から求めたものなので、低温ほど実際のモルエントロピーとの差は大きくなると予想されます。
横軸に絶対温度、縦軸にモルエントロピーをとると、その概形はこちらのようになります。

赤が実際の値で、青が十分に高温であるとして近似をしたものです。
厳密なモルエントロピーは、分光法などによって得られたエネルギー準位から、級数の和として分子分配関数を計算することで求められます。
絶対零度近傍でモルエントロピーは\(0\)になるはずですが、近似を行った場合はエントロピーが\(-\infty\)へ発散するため、大きな差が生じます。
温度が高くなるにつれて、実際のモルエントロピーも単純な対数のグラフへと近づいていきます。
振動運動による寄与
最後に、振動運動による寄与を求めます。
まず、一次元調和振動子のエネルギー準位間の差である\(\hbar \omega\)を\(\varepsilon\)と表すことにします。
すると、振動分配関数\(q^\rm{V}\)\(\displaystyle =\frac{1}{1-\exp{(-\beta \varepsilon)}}\)、平均振動エネルギー\(\varepsilon^\rm{V}\)\(\displaystyle =\frac{\varepsilon}{\exp{(\beta \varepsilon)}-1}\)と書けます。
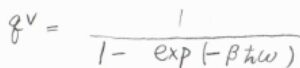
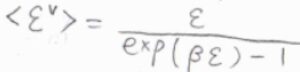
平均エネルギー導出の過程は、こちらの動画を参照してください。

この結果を利用すると、まず、モルエントロピーの第一項である\(\displaystyle \frac{U_\rm{m}(\mathit{T})-\mathit{U}_\rm{m}(0)}{T}\)は、\(N_\rm{A}\)\(\langle \varepsilon^\rm{V}\rangle\)\(k_\rm{B}\)\(\beta\)と変形できます。
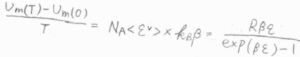
ここで、\(k_\rm{B}\)\(\displaystyle \beta=\frac{1}{T}\)です。
\(\langle \varepsilon^\rm{V}\rangle\)\(\displaystyle =\frac{\varepsilon}{\exp{(\beta \varepsilon)}-1}\)を代入して整理すると、\(\displaystyle \frac{U_\rm{m}(\mathit{T})-\mathit{U}_\rm{m}(0)}{T}=\frac{R\beta \varepsilon}{\exp{(\beta \varepsilon)}-1}\)となります。
そして、エントロピーの式の右辺第二項の\(q\)に\(q^\rm{V}\)\(\displaystyle =\frac{1}{1-\exp{(-\beta \varepsilon)}}\)を代入すると、モルエントロピー\(S_\rm{m}\)\(^\rm{V}\)\((T)\)は、\(\displaystyle \frac{R\beta \varepsilon}{\exp{(\beta \varepsilon)}-1}-R\ln{[1-\exp{(-\beta \varepsilon)}]}\)と導かれます。
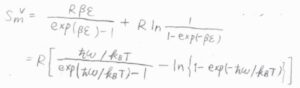
\(\varepsilon=\hbar \omega\)、\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)を代入すると、\(S_\rm{m}\)\(^\rm{V}(\mathit{T})=\)\(\displaystyle \frac{R\hbar \omega/k_\rm{B}\mathit{T}}{\exp{(\hbar \omega/k_\rm{B}\mathit{T})}-1}-R\ln{[1-\exp{(-\frac{\hbar \omega}{k_\rm{B}\mathit{T}})}]}\)となります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




