こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Nernst equation)
それでは内容に入っていきます!
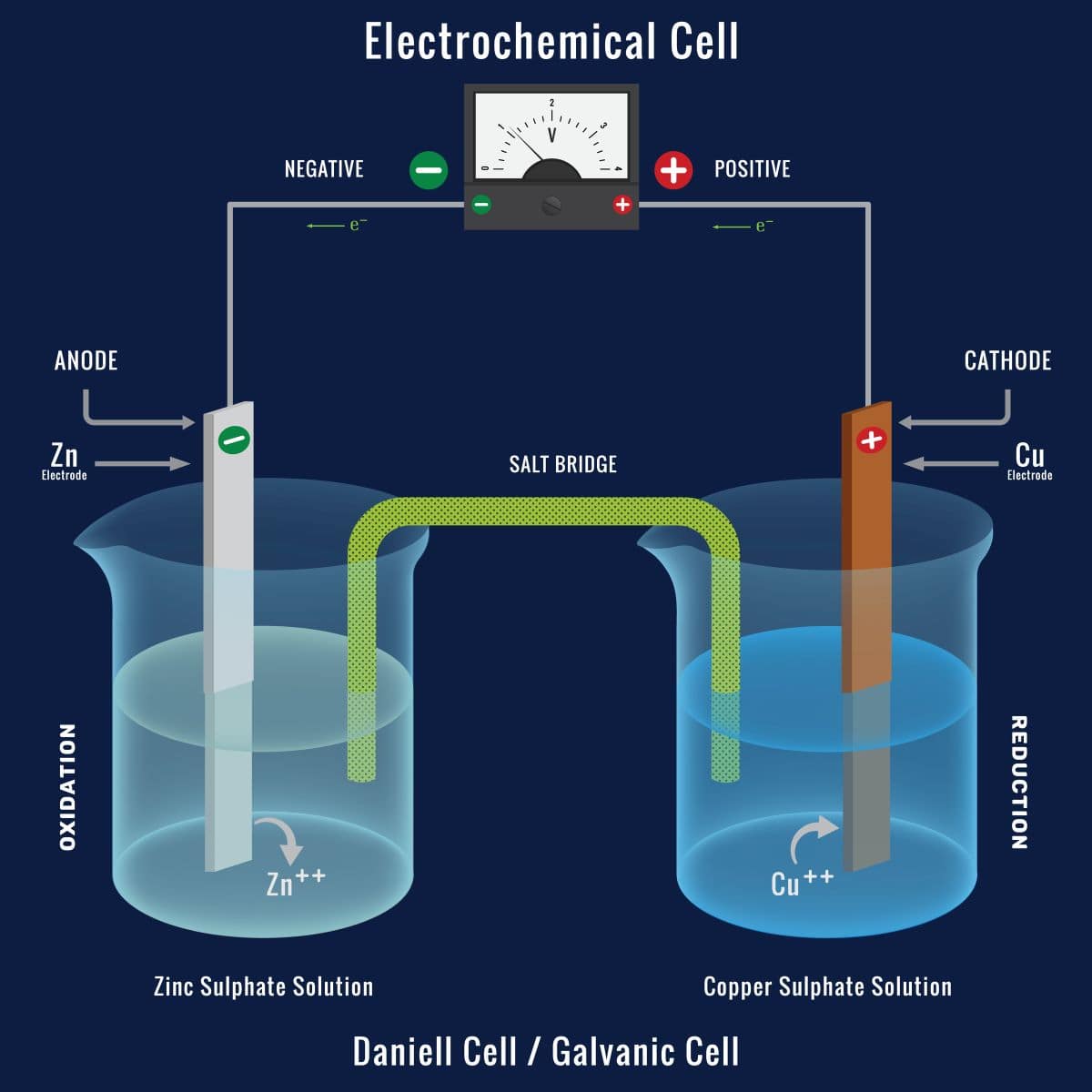
電気化学セル
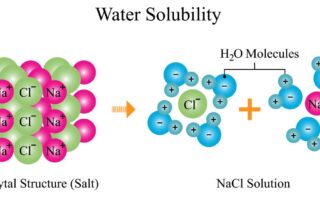
まず化学エネルギーを電気エネルギーへと変換させるものとして、広く使われている電池は、化学電池とも呼ばれます。
また、これらはガルバ二電池というものに該当します。
ガルバ二電池とは、異種の電気伝導体の相が直列につながれており、そのうち少なくとも一方はイオン伝導体の相で、両端の相が同じ化学的組成の電気伝導体であるものとする説と、化学電池そのものとする説があります。
いずれにしてもボルタ電池とかダニエル電池などのように、何か特定の電池を指す言葉ではありません。
これと似たもので電解槽というものがあります。
これは、電池とは反対に電気エネルギーを利用して化学反応を起こす仕組みです。
これらはいずれも電極2つと電解質によって構成されており、これらをまとめて電気化学セルと呼びます。
極性の定義
これらの電極には名前が付いており、高校や中学で習うときには、電池の電極を正極、負極と呼び、電解槽の電極を陽極、陰極と呼ぶことになっています。
英語でいうとカソードとアノードの2種類の単語があり、先ほどの電極がどのように対応しているのかは、定義によって異なります。

まず、電流の流れる向きによって定義する場合は、外部回路から電流が流入する電極のことをアノードと呼び、外部回路へ電流が流出する電極のことをカソードと言います。
電気分解では、正極と陽極がアノード、負極と陰極がカソードと同じ意味になります。
電池では、負極と陽極がアノード、正極と陰極がカソードになります。
電位差に着目した場合は、電解質から電極へ電子が流入してくる電極のことをアノードと呼び、電極から電解質へと電子を放出する電極のことをカソードと言います。
電気分解では、定義によって変化せず、正極と陽極がアノード、負極と陰極がカソードになります。
電池では、負極と陰極がアノードで、正極と陽極がアノードと同じ意味になります。
これ以降は、後者の定義で呼称することにします。
半反応
そして、それぞれの電極の周辺で起こっている反応のことは、半反応と言います。
それ単独では、半反応は起こらず、対をなすもう一方の電極でも何らかの反応が起こっていないといけないという点で、一般的な化学反応とは区別されます。
電子のやり取りをしているということから、電極周辺で起こる半反応は酸化反応か還元反応になります。
その一般式は、このようになります。
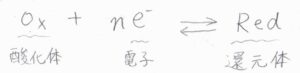
\(\rm{Ox}\)が酸化体、\(\rm{Red}\)が還元体です。
1つの半反応で関係づけられる酸化体と還元体の関係は「共役である」といい、\(\rm{Ox/Red}\)というような表記をします。
隔膜と塩橋
さて電池には、さまざまな分類があるわけですが、電気回路を閉じるための手段について見ていきます。
それぞれの電極で異なるものを用いる場合、それらが混合しないようにしつつ、電気回路を閉じる必要があります。
そのときに、使われる代表的なものが隔膜と塩橋です。
隔膜
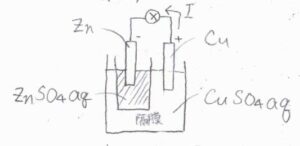
隔膜はセパレーターとも呼ばれ、セラミックやセロハン、ポリオレフィンなど多孔質膜や不織布が使われます。
異なる電解液同士の界面の総称を液絡といい、隔膜は液絡の一種になります。
上の図は、アノードを亜鉛、カソードを銅としたダニエル電池を例として表したものです。
亜鉛電極と硫酸亜鉛水溶液、銅電極と硫酸銅水溶液のセットは半電池と呼ばれます。
隔膜の穴の大きさを小さくすると、特定のイオンだけを透過させることができます。
イオン濃度に差があることで生じる電位差を液間電位差と言います。
穴が大きいと、それだけイオンが速く透過しやすくなるため、電流の値が大きくなりますが、大きすぎるとほかのイオンも透過するようになって、自己放電やショートを引き起こします。
電解質溶液の種類が異なる場合だけではなく、同じ電解質溶液で濃度が異なる場合や気体電極で圧力が異なる場合、アマルガムなどの溶液の電極で濃度が異なる場合も隔膜が使われます。
こういった電池のことは電解質濃淡電池、電極濃淡電池と言います。
塩橋
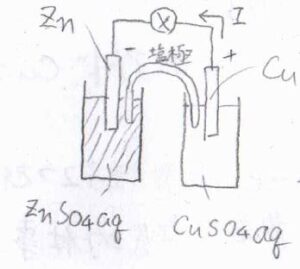
一方の塩橋とは、異なる液体同士を完全に隔離した状態、つまり界面がない状態で液間電位差をほとんど生じさせずに接続するものです。
よく例として挙げられるのは、\(\rm{KCl}\)や\(\rm{KNO_3}\)などの水溶液でU字型の管を満たし、それを寒天などで凝固させたものです。
用いる塩のカチオンとアニオンの移動度が大きく異なると、液間電位差を生じさせる原因となるため、これらは同程度の移動度をもっていることが望ましいとされています。
塩橋がないとどうなるかというと、例えばカソード周辺で\(\rm{Cu}\)\(^{2+}\)が還元されたとしましょう。

すると、対をなすアニオンの分だけ、溶液全体が負に帯電することになります。
電気的中性の原理より、実際にはこのようなことは起こらないので、電池としては機能しません。
そこにたとえば\(\rm{KCl}\)水溶液を固めた塩橋があると、\(\rm{K}\)\(^+\)が電解液へと溶け込むことで電気的中性となるので、電池として機能するようになります。
電池式
これらの電池は、電池式と呼ばれるもので表記します。
ダニエル電池は、隔膜を用いた場合は上側のように、塩橋を用いた場合は下側のように表記します。
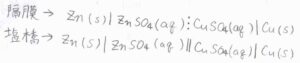

まず、|が界面を表します。
例えば、固体である亜鉛電極と硫酸亜鉛溶液は異なる相であるので、一本線を引きます。
それから、⋮は液絡を指しますので、2つの電解液の間に⋮を書きます。
||は液間電位差が除かれたとできる接続を指すもので、塩橋が該当します。
イオン化傾向と電位の関係
続いて、電池の電圧がどのようにして決まるのかという話をしていきます。
まず、高校で習ったイオン化傾向を思い出してみましょう。
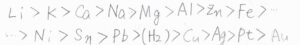
この中で、リチウムが最もカチオンになりやすく、金が最もなりにくいということになります。
還元反応の起こりやすさを考えた場合には、イオン化傾向が大きいほど酸化体が安定となるので、電解質から電子を受け取りやすい、つまりアノード側になりやすいことになります。
ダニエル電池で亜鉛と銅を比べた場合、亜鉛の方がイオン化傾向が大きいので、亜鉛がアノード、銅がカソードになります。
2つの電極について還元反応の起こりやすさから電位を考えると、この図のようになります。
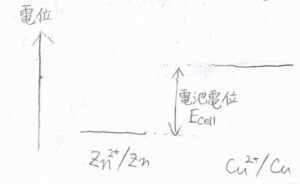
イオン化傾向が大きいアノード側がより低い電位となります。
そして、アノードとカソードの電位差が電池の電圧になります。
これを電池電位もしくは起電力といい、ここでは\(E_\rm{cell}\)と表すことにします。
\(-e\)という負電荷をもつ粒子を2つ移動させるのに必要な電気的仕事は\(-2eE_\rm{cell}\)であり、これは負の値をとります。
電子の移動は自発的な変化であり、系は外部へ仕事をすることになります。
可逆系において、ギブズエネルギー変化は、膨張を伴わない仕事に等しいということから、反応ギブズエネルギー\(\Delta_\rm{r}\)\( G=-nFE_\rm{cell}\)となります。
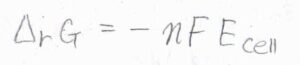
\(n\)は電池全体の酸化還元反応式の中でやりとりされる電子の個数、\(F\)はファラデー定数です。
ここで注意したいのは、電池電位\(E_\rm{cell}\)自体は測定可能な量であるのに対して、それぞれの電極の電位はそれ単独では決められないということです。
電気的中性の原理があるので、イオンはそれ単独で生成させることができず、対イオンも同時に必ず生成します。
したがって、イオンの生成ギブズエネルギー\(\Delta_\rm{f}\)\( G\)は1つに決まらず、電極の電位も決まりません。
そこで、一般的には\(1\ \rm{atm}\)において、水和した水素イオンが\(1\ \rm{mol}\)生成するときのギブズエネルギー変化を基準として、その値との差をそのイオンの生成ギブズエネルギーとします。
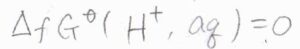
これにならうと、水素イオンの還元反応の電位は\(0\ \rm{V}\)となり、これより任意の電極の電位も決定することができます。
そのときの電極の電位は、もう一方の半反応が標準圧力における\(2\rm{H}\)\(^++2\rm{e}\)\(^- \longrightarrow \rm{H}_2\)であるときの電池電位\(E_\rm{cell}\)に等しいということになります。
また、このときの\(E_\rm{cell}\)は、\(\displaystyle -\frac{\Delta_\rm{f}\mathit{G}}{\mathit{nF}}\)とも書けます。
基準となる電極は、基準電極もしくは参照電極や照合電極などと呼ばれます。
活量\(1\)の水素イオンの還元反応を半反応とする基準電極を標準水素電極、略してNHEもしくはSHEと言います。
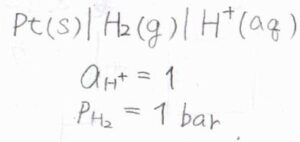
気体の圧力は\(1\ \rm{atm}\)で、あらゆる温度でその電位を\(0\ \rm{V}\)と定めます。
もちろん、基準電極に選ばれる電極は標準水素電極だけではなく、ほかには銀-塩化銀電極やカロメル電極などがあります。
\(\rm{pH}\)\(=0\)の標準水素電極ではなく、実際の電解液の\(\rm{pH}\)に合わせた可逆水素電極を基準電極とすることもあります。
半電池の電池電極のことは、電極電位もしくは単極電位と言います。
特に、標準状態において、標準水素電極を基準としており、かつすべての化学種の活量が\(1\)であるときの電極電位を標準電極電位や標準還元電位、標準電位などと呼びます。
標準電極電位とイオン化傾向を照らし合わせると、水素よりもイオン化傾向が大きいものについては標準電極電位が負の値となり、水素で\(0\)、水素よりもイオン化傾向が小さいものについて正の値をとるということになります。
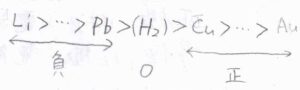
ネルンストの式
ここからは、活量と電池電位の関係について、考えていきましょう。
まず、アノード側、カソード側、そして電池全体で起こる酸化還元反応をこのように表すことにします。
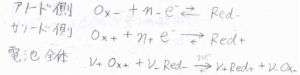
アノード側、カソード側の反応ギブズエネルギーをそれぞれ\(\Delta_\rm{r}\)\( G_+\)、\(\Delta_\rm{r}\)\( G_-\)とすると、全体の反応ギブズエネルギー\(\Delta_\rm{r}\)\( G\)は、\(\nu_+\Delta_\rm{r}\)\( G_+-\nu_-\Delta_\rm{r}\)\( G_-\)と書けます。
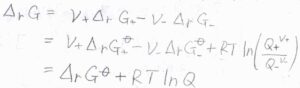
さらに、それぞれの酸化体と還元体の活量の比を反応商\(Q_+\)、\(Q_-\)として、\(\displaystyle \frac{Q_+}{Q_-}\)を\(Q\)と表すと、\(\Delta_\rm{r}\)\( G=\Delta_\rm{r}\)\( G^\circ+RT\ln{Q}\)と書けます。
ここで、\(\Delta_\rm{r}\)\( G^\circ\)は標準反応ギブズエネルギー、\(R\)は気体定数、\(T\)は絶対温度です。
電池電位\(E_\rm{cell}\)は、\(\displaystyle -\frac{\Delta_\rm{r}\mathit{G}}{\mathit{nF}}\)で与えられます。
したがって、\(E_\rm{cell}\)\(\displaystyle =-\frac{\Delta_\rm{r}\mathit{G}^\circ}{\mathit{nF}}\)\(\displaystyle -\frac{RT}{nF}\ln{Q}\)となります。

\(\displaystyle -\frac{\Delta_\rm{r}\mathit{G}^\circ}{\mathit{nF}}\)を\(E_\rm{cell}\)\(^\circ\)と書き換えると、\(E_\rm{cell}\)\(=E_\rm{cell}\)\(\displaystyle ^\circ-\frac{RT}{nF}\ln{Q}\)となります。
ここで、\(E_\rm{cell}\)\(^\circ\)は標準電池電位と呼ばれ、すべての化学種の活量が\(1\)であるときの電池電位を表します。
一方の半電池が標準水素電極のときには、電極電位を\(E\)、標準電極電位を\(E^\circ\)として、\(\displaystyle E=E^\circ+\frac{RT}{nF}\ln{(\frac{a_\rm{Ox}}{\mathit{a}_\rm{Red}})}\)と書けます。
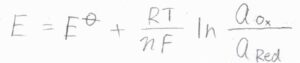
この式はネルンストの式と呼ばれ、電気化学の根幹となるとても重要な式です。
\(a_\rm{Ox}\)と\(a_\rm{Red}\)は、それぞれ酸化体と還元体の活量です。
時間の経過とともに反応が進行すると、活量の比が変化することで、電極電位も変化します。
乾電池を長時間使うと、ある時点から電流が流れなくなる、いわゆる電池切れの状態は、活量が変化することでカソードの電極電位とアノードの電極電位が等しくなった状態です。
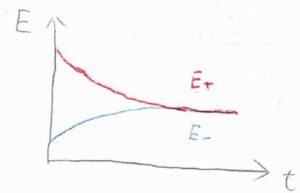
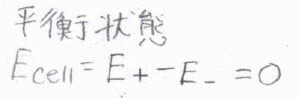
これは、電池全体の酸化還元反応が化学平衡に達した状態とも言えます。
平衡定数\(K\)は、電池電位が\(0\ \rm{V}\)のときの反応商であり、\(\displaystyle \exp{(\frac{nFE_\rm{cell}^\circ}{\mathit{RT}})}\)と書けます。
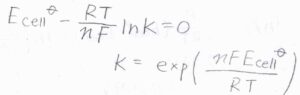
また、平衡定数から反応エンタルピーが求められたのと同様に、標準電池電位からも反応エンタルピーを求めることができます。
熱力学基本式より\(\displaystyle (\frac{\partial G}{\partial T})_p=-S\)となるので、\(\displaystyle \frac{\rm{d}(\mathit{E}_{cell}^\circ)}{d\mathit{T}}=\frac{\Delta_r \mathit{S}^\circ}{\mathit{nF}}\)という関係が成り立ちます。
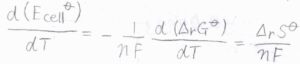
ここで、\(S\)はエントロピーです。
平衡定数と同じく標準電池電位も圧力に依存しないため、これは偏微分ではなく全微分になります。
この関係を使うと、標準反応エンタルピー\(\Delta_\rm{r}\)\(\displaystyle H=-nF[E_\rm{cell}\)\(\displaystyle ^\circ-T(\frac{\rm{d}(\mathit{E}_{cell}^\circ)}{d\mathit{T}})]\)となります。
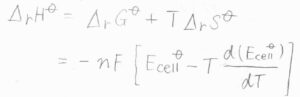
熱量を測定せずとも、\(E_\rm{cell}\)\(^\circ\)がわかれば、そこからイオンの生成エンタルピーも求めることができます。
活量係数と電池電位の関係
電池電位がわかれば、塩の濃度が低いときの活量係数を求めることもできます。
ここでは、電解質を\(\rm{HCl}\)として、一方が標準水素電極、もう一方が銀-塩化銀電極である電池を考えます。
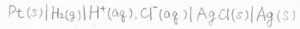
ネルンストの式を使うと、電池電位\(E_\rm{cell}\)は、それぞれの化学種の活量を使って、このように表されます。
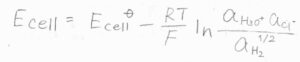
固体である塩化銀の活量が書かれていませんが、これは活量の定義として、固体の活量は\(1\)とされているためです。
溶媒が反応に関わるときにも、多くの場合、溶媒の活量を\(1\)と考えます。
水素ガスの活量も\(1\)で一定であると考えられるときには、
\(E_\rm{cell}\)\(=E_\rm{cell}\)\(\displaystyle ^\circ-\frac{RT}{F}\ln{(a_\rm{H_3O^+}\mathit{a}_\rm{Cl^-})}\)となります。
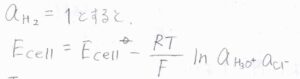
ヒドロニウムイオンと塩化物イオンの活量係数の幾何平均を平均活量係数\(\gamma_\pm\)、\(\rm{HCl}\)の質量モル濃度を\(b\)と表すことにすると、\(E_\rm{cell}\)\(=E_\rm{cell}\)\(\displaystyle ^\circ-\frac{2RT}{F}[\ln{(\frac{b}{b^\circ})}+\ln{\gamma_\pm}]\)と書けます。
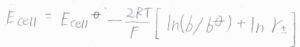
ここで、\(\rm{HCl}\)の濃度は十分に低いとして、デバイ-ヒュッケルの極限法則が成り立つものとします。
そのとき、\(\log{\gamma_\pm}=-A|z_+z_-|I^{1/2}\)となります。

\(A\)は溶媒と温度に依存する定数で、\(z\)はイオンの価数、\(I\)はイオン強度です。
詳しくは、こちらを参照してください。
今回の場合は、カチオンとアニオンの価数がいずれも\(1\)であるため、\(\displaystyle I=\frac{b}{b^\circ}\)となります。
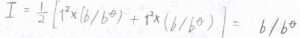
これを代入して整理すると、
\(E_\rm{cell}\)\(\displaystyle +\frac{2RT}{F}\ln{(\frac{b}{b^\circ})}=E_\rm{cell}\)\(\displaystyle ^\circ-\frac{2ART\ln{10}}{F}(\frac{b}{b^\circ})^{1/2}\)という関係が導かれます。
この式の左辺を\(y\)とおき、縦軸を\(y\)、横軸を\(b^{1/2}\)としてグラフを書くと、一次関数になります。
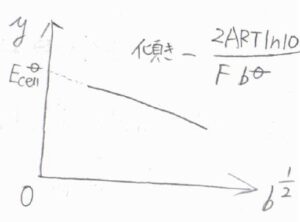
このグラフの\(y\)切片が銀-塩化銀電極の標準電極電位となります。
標準電極電位がわかれば、\(\displaystyle \ln{\gamma_\pm}=\frac{F}{2RT}(E_\rm{cell}\)\(^\circ-E_\rm{cell}\)\(\displaystyle )-\ln{(\frac{b}{b^\circ})}\)という関係式に、質量モル濃度\(b\)とそのときの電池電位\(E_\rm{cell}\)を代入することで、活量係数を求めることができます。
練習問題
それでは最後に練習問題をやってみましょう。
1. 一方が亜鉛電極、もう一方が銀-塩化銀電極の電池がありました。
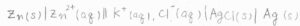
\(25^\circ\rm{C}\)における標準電極電位は、銀-塩化銀電極が\(0.222\ \rm{V}\)、亜鉛電極が\(-0.763\ \rm{V}\)です。
亜鉛(II)イオンと塩化物イオンの活量がいずれも\(0.1\)であるときの電池電極はいくらになるでしょうか。
また、標準電池電位と平衡定数も求めてください。
2. 温度\(25^\circ \rm{C}\)で質量モル濃度が\(9.138\times 10^{-3}b^\circ\)の塩酸で、電池電位が\(0.4686\ \rm{V}\)となりました。
標準電池電位が\(0.2232\ \rm{V}\)とわかっているとき、平均活量係数\(\gamma_\pm\)はいくらになるでしょうか。
必要であれば、以下の数値を用いてよいとします。

やりとりされる電子の数を2個に合わせて全体の酸化還元反応の式を書くと、下のようになります。

まず、標準電極電位が与えられているので、これらの差から標準電池電位が求められます。
その値は、\(0.222\ \rm{V}\)\(-(-0.763\ \rm{V}\)\()=0.985\ \rm{V}\)となります。
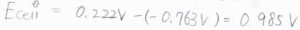
電位はあくまで電荷\(1\ \rm{C}\)あたりの仕事なので、電子の個数を係数につけることがないように注意してください。
次に、イオンの活量がいずれも\(0.1\)であるときの電極電位をネルンストの式を用いて計算します。
まず、アノードの電極電位は、\(-0.763\ \rm{V}\)\(-0.030\ \rm{V}\)より、\(-0.793\ \rm{V}\)となります。
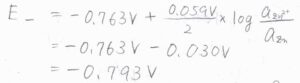
同様に、カソードの電極電位は\(0.281\ \rm{V}\)と求まります。
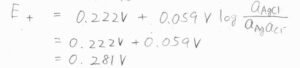
したがって、電池電位は\(1.074\ \rm{V}\)となります。
![]()
平衡定数\(K\)は、電池電位が\(0\ \rm{V}\)であるときの反応商であるため、\(10^{33.4}\)と計算されます。
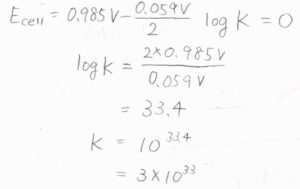
概算すると、これは\(3\times10^{33}\)です。
2. 平均活量係数と電池電位の関係式に、与えられている値を代入していきます。
すると、\(\ln{\gamma_\pm}=-0.07993\)となります。

したがって、\(\gamma_\pm=0.9232\)と計算されます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!