こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(hypervalent molecule)
それでは内容に入っていきます!
超原子価化合物
突然ですが、硫酸の構造式をご存じですか?
正解はこれです。
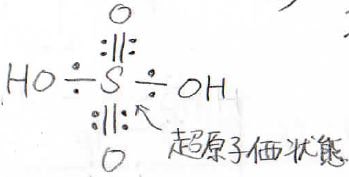
高校までだと、この構造はあまり見かけなかった気がします。
このように形式的に原子価殻に9個以上の電子を持つ典型元素を含む化合物は、超原子価化合物と呼ばれます。
また、そのようになっている原子の状態を超原子価状態と言います。
最外殻の電子数は8個になるというオクテット則(8電子則)に従いません。

超原子価化合物には、以下のような物質が該当します。
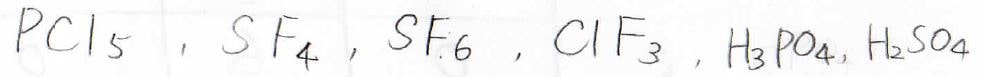
中には、5本以上の腕をもっているものもあります。
ここで問題なのが、これらがどんな立体構造を持っているのかということです。
有機化合物の立体構造を考えるときには混成軌道の考え方が有用でしたが、これでは4本腕までしか考えられません。
混成軌道については、こちらの記事をご覧ください。

この記事では、より一般的に化合物の立体構造を考える方法について、お話ししていきます。
電子間反発が小さい立体構造
基本的な考え方は、混成軌道の立体的な配置を考えたときとまったく同じで、何方向に電子対が向くのかということから、最も電子間反発が小さい立体構造を考えます。
その対応表がこちらです。

\(\displaystyle n\)が電子対数、ここでは電子対が向く方向の数だと考えてください。
\(\displaystyle n=2\sim 4\)のときは、混成軌道と同じです。
\(\displaystyle n\)がこれより大きくなると、三角両錐などという聞きなれない形をとるようになります。
試しに、この対応表を使って化合物の立体構造を予測してみましょう。
まず、五塩化リンです。
共有電子対(bp)が\(\displaystyle 5\)、孤立電子対(lp)が\(\displaystyle 0\)で、合計は\(\displaystyle 5\)です。
したがって、三角両錐型分子になります。

六フッ化硫黄では共有電子対が\(\displaystyle 6\)つ、孤立電子対が\(\displaystyle 0\)で、その合計は\(\displaystyle 6\)です。
このような八面体型分子だとわかります。
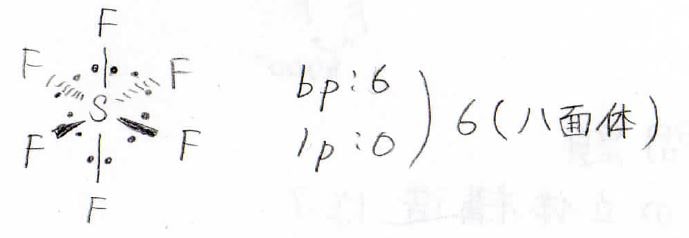
孤立電子対があるとき
孤立電子対があるときには、少し複雑化します。
というのが、三角両錐型や五角両錐ではすべての電子対が等価ではないためです。
孤立電子対の位置が何通りか考えられるようになってしまいます。
VSEPR則
本当に安定な構造はどれなのかを考えるときに有用なのがVSEPR則です。
これはValence Shell Electron Pair Repulsion(原子価殻電子対間反発)の略です。
難しい言葉ですが、その考え方は次のようなものです。
- 電子対間の反発は、その電子対の属性(共有か孤立か)の組み合わせで変わる
- 電子対間の反発の大小関係は、bp-bp < bp-lp < lp-lpである
- 化合物は最も電子対間反発が小さい立体構造をとる
四フッ化硫黄の例で、実際に考えてみましょう。
共有電子対は\(\displaystyle 4\)、孤立電子対が\(\displaystyle 1\)で合計が\(\displaystyle 5\)になります。
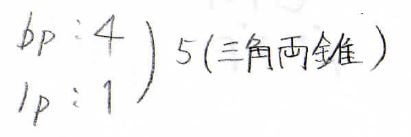
したがって、電子対は三角両錐型に配置されます。
しかし、考えられる構造は、次のように2通り出てきます。
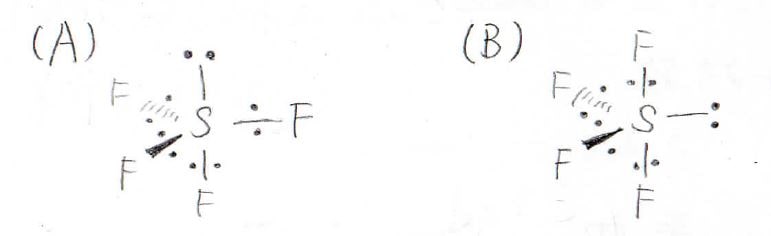
ここでVSEPR則に基づき、電子対間反発を考えていきます。
2つの電子対がなす角度が\(\displaystyle 120^\circ\)、\(\displaystyle 180^\circ\)のときは、その反発を無視できるものとして、\(\displaystyle 90^\circ\)の関係にある電子対間の反発のみを考えることにします。
実際に数えたのが、こちらの表です。
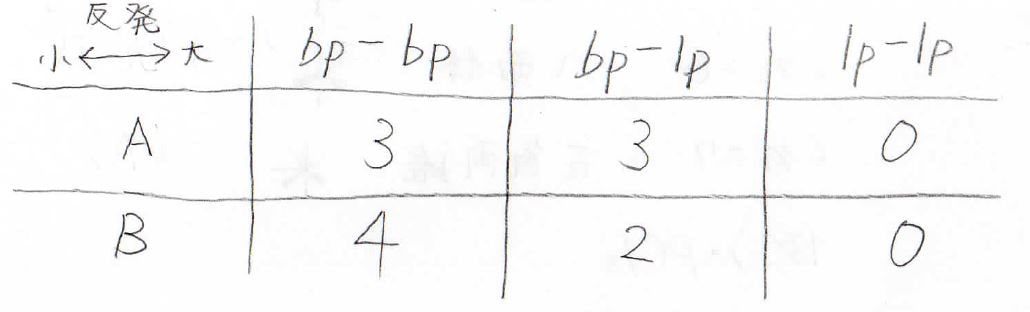
両者を比較すると、\(\displaystyle \rm{B}\)が\(\displaystyle \rm{A}\)よりも\(\displaystyle E_\rm{bp-lp}\)\(-E_\rm{bp-bp}\)だけ安定であることがわかります(\(\displaystyle E\)は反発のエネルギー)。
したがって、\(\displaystyle \rm{B}\)の構造であることがわかり、原子だけを見たときには、シーソー型の分子となります。

練習問題
最後に、練習問題をやってみましょう。
三フッ化塩素の立体構造を考えてみてください。

まずは電子対の数を数えます。
共有電子対が\(\displaystyle 3\)、孤立電子対が\(\displaystyle 2\)、その合計は\(\displaystyle 5\)です。
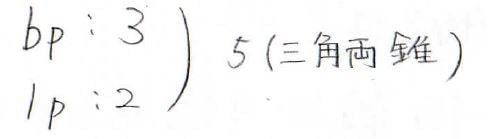
したがって、電子対は三角両錐型に配置されます。
どこに孤立電子対があるのか、考えられる構造は、次の3パターンがあります。

\(\displaystyle 90^\circ\)の関係にある電子対の組を数えると、このようになります。
これより以下のことが言えます。
- \(\displaystyle \rm{A}\)は\(\displaystyle \rm{B}\)より\(\displaystyle E_\rm{lp-lp}\)\(-E_\rm{bp-lp}\)だけ安定
- \(\displaystyle \rm{A}\)は\(\displaystyle \rm{C}\)より\(\displaystyle 2(E_\rm{bp-lp}\)\(-E_\rm{bp-bp}\)\()\)だけ安定
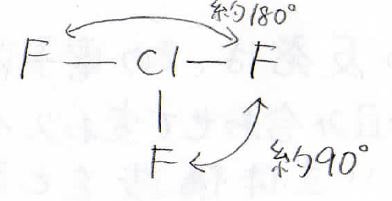
したがって、三フッ化塩素は\(\displaystyle \rm{A}\)の立体構造をとることになります。
原子だけを見ると、T字型分子になります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!