こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(equilibrium)
それでは内容に入っていきます！
化学平衡とは
はじめに、化学平衡とはどんな状態かを確認しましょう。
言葉でいうと、順反応と逆反応が同時に起こって、見かけ上は反応が起こっていないようになる現象のことを言います。
ここでは化学種\(\rm{A}\)\(\)ひとつから化学種\(\rm{B}\)\(\)ひとつに変化する反応を順反応として、\(\rm{A}\)\(\)と\(\rm{B}\)\(\)の混合系について考えてみましょう。
熱力学基本式より、ギブズエネルギーの微小変化\(\rm{d}\)\(G\)は、\(-S\rm{d}\)\(T+V\rm{d}\)\(p+\mu_\rm{A}\)\( \rm{d}\)\(n_A+\mu_\rm{B}\)\( \rm{d}\)\(n_B\)となります。
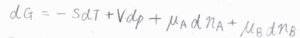
\(S\)はエントロピー、\(T\)は絶対温度、\(V\)は体積、\(p\)は圧力、\(\mu\)は化学ポテンシャル、\(n\)は物質量です。
反応が起こる前と後で、温度と圧力に変化がなかったとき、\(\rm{d}\)\(G=\mu_\rm{A}\)\(\rm{d}\)\(n_\rm{A}\)\(+\mu_\rm{B}\)\(\rm{d}\)\(n_\rm{B}\)\(\)と書けます。
\(\rm{A}\)\(\)が消費された分だけ\(\rm{B}\)\(\)が増えることから、\(\rm{d}\)\(n_\rm{A}\)\(=\rm{d}\)\(n_\rm{B}\)\(\)であり、これを\(\rm{d}\)\(n\)とおくと、\(\rm{d}\)\(G=(\mu_\rm{A}\)\(-\mu_\rm{B}\)\()\rm{d}\)\(n\)となります。
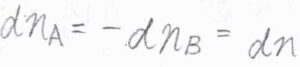
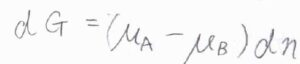
\(\mu_\rm{A}\)\(=\mu_\rm{B}\)\(\)のときには、\((\partial G/\partial n)_T,p=0\)であり、この組成でギブズエネルギーは極値をとりうることになります。
極小となるとき、その組成から左に動いても右に動いても、ギブズエネルギーが増大します。
つまり熱力学的には不利となりますから、見かけ上はその組成から変化しなくなります。
これが化学平衡です。
つまり、化学平衡となることの必要条件が、\(\mu_\rm{A}\)\(=\mu_\rm{B}\)\(\)となります。
化学平衡では微少量ではなく、反応前後のモルギブズエネルギー変化\(\Delta_\rm{r}\)\( G\)も\(0\)となります。
\(\Delta_\rm{r}\)\( G\)が負のときには、順反応が自発的に起こりうるということになり、これをエキサゴニックと言います。
\(\Delta_\rm{r}\)\( G\)が正のときは、逆反応が自発的に起こりうるということで、これをエンダーゴニックと言います。
順反応を起こすためには、外界から仕事をする必要があります。
平衡定数とギブズエネルギーの関係
ここからは、化学反応を一般化して考えていきます。
小文字を化学量論係数、大文字を化学種として、以下のような化学反応があったとします。
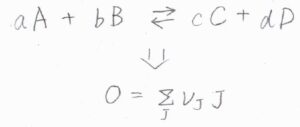
これを一般化して\(0=\Sigma_ \rm{J}\)\( \nu_\rm{J}\)\( \rm{J}\)\(\)と表すことにします。
\(\rm{J}\)\(\)が化学種、\(\nu_\rm{J}\)\(\)は化学量数です。
化学量数は、化学量論係数を反応系について負となるようにとったものです。
混合系として見て、全体のギブズエネルギーの微小変化\(\rm{d}\)\(G\)は、\((\Sigma_\rm{J}\)\( \nu_\rm{J}\)\( \mu_\rm{J}\)\()\rm{d}\)\(\xi\)と書けます。
ここで、\(\xi\)は反応進行度と呼ばれます。
任意の化学種\(\rm{J}\)\(\)について、\(\rm{d}\)\(n_\rm{J}\)\(=\nu_\rm{J}\)\( \rm{d}\)\(\xi\)となるように定義した値です。
化学種\(\rm{J}\)\(\)について、\(|\nu_\rm{J}\)\(|\ \rm{mol}\)\(\)あたりの反応ギブズエネルギー\(\Delta_\rm{r}\)\( G\)は、\(\Sigma_\rm{J}\)\(\nu_\rm{J}\)\(\mu_\rm{J}\)\(\)であり、これを活量\(a_\rm{J}\)\(\)を使って書くと、標準反応ギブズエネルギー\(\Delta_\rm{r}\)\( G^\circ\)から\(RT\ln{\Pi_\rm{J}\mathit{a}_J^{\mathit{\nu}_J}}\)だけ変化した値だとわかります。
\(\Pi_\rm{J}\)\(a_\rm{J}\)\(^{\nu_\rm{J}}\)は、反応商と呼ばれます。
これを\(Q\)とおき、平衡状態に達したときの\(Q\)を\(K\)と表すことにすると、\(\Delta_\rm{r}\)\( G^\circ+RT\ln{K}=0\)より、\(K=\exp{(-\Delta_\rm{r} \mathit{G}^\circ/\mathit{RT})}\)となります。
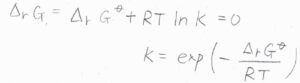
これが標準反応ギブズエネルギー\(\Delta_\rm{r}\)\( G^\circ\)と平衡定数である\(K\)の関係です。
活量やフガシティーといった実効の量を使って記述された平衡定数は、特に熱力学的平衡定数と呼ばれます。
標準反応ギブズエネルギーは、それぞれの化学種の標準生成ギブズエネルギー\(\Delta_f G_\rm{J}^\circ\)から計算可能であるため、その温度と圧力での値がわかれば、平衡定数もわかることになります。
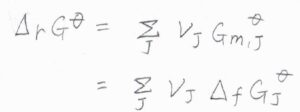
いろいろな平衡定数の表し方
それで、活量は、他の濃度を表すパラメータを使って表すことができるので、そのパラメーターを用いた平衡定数というのも考えることができます。
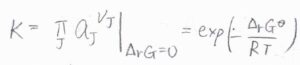
具体的には、このようにモル分率、蒸気圧、モル濃度、質量モル濃度などがあります。
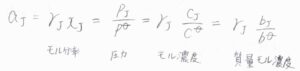
いま、それぞれを\(x\)、\(p\)、\(c\)、\(b\)と表すことにしています。
仮にモル分率を用いて表した平衡定数を\(K_x\)とした場合、活量を用いた\(K\)との関係は、\(K=K_\gamma K_x\)となります。
\(K_\gamma\)は、活量係数だけを取り出したものです。
同様にそれぞれの平衡定数が標準濃度によって変化しないときには、\(K=K_p=K_\gamma K_c=K_\gamma K_b\)となります。
しかし、実際には\(K_\gamma\)の計算は複雑になることが多いので、ほとんど\(1\)と大差ないと考えることも多いです。
前回導いた低濃度のイオンの活量係数は、デバイ-ヒュッケルの極限法則よりこのように書けますが、濃度によってイオン強度が変化して、それの指数をとる形になります。
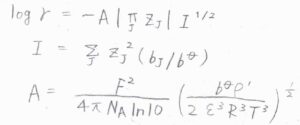
詳しくは、こちらを参照してください。
\(K_\gamma=1\)と考えた場合、\(K=K_x=K_p=K_c=K_b\)となります。
標準モル濃度に依存する場合についても、たとえば蒸気圧とモル濃度は理想気体を仮定すれば、このように平衡定数の換算ができます。
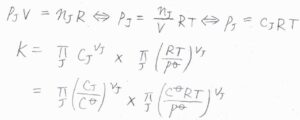
まず、理想気体の状態方程式より、\(p_\rm{J}\)\(=c_\rm{J}\)\(RT\)となります。
これより、平衡定数\(K=K_c \Pi_\rm{J}\)\((c^\circ RT/p^\circ)^{\nu_\rm{J}}\)\(\)となります。
第二項のかっこの中は定数であるため、\(\Sigma_\rm{J}\)\( \nu_\rm{J}\)\(\)を\(\Delta \nu\)とすると、\(K=K_c (c^\circ RT/p^\circ)^{\Delta \nu}\)となります。
標準圧力を\(10^5\ \rm{Pa}\)\(\)、標準質量モル濃度を\(1\ \rm{mol\ dm}\)\(^{-3}\)としたときには、\(K=K_c (T/12.0\ \rm{K}\)\()^{\Delta \nu}\)という関係になります。
これが標準の濃度に依存しないときというのは、\(\Delta \nu=0\)のときです。
つまり、反応により化学種の数量が変化しないときです。
平衡定数の分子論的解釈
最後、少し分子論的な話をして終わります。
温度圧力一定条件で標準反応ギブズエネルギー\(\Delta_\rm{r}\)\( G^\circ\)は、\(\Delta_\rm{r}\)\( H^\circ-T\Delta_\rm{r}\)\( S^\circ\)となります。
\(\Delta_\rm{r }\)\(H^\circ\)は標準反応エンタルピー、\(\Delta_\rm{r}\)\( S^\circ\)は標準反応エントロピーです。
したがって、平衡定数\(K=\exp{(-\Delta_\rm{r} \mathit{H/RT})}\times \exp{(\Delta_\rm{r} \mathit{S/R})}\)と書けます。
たとえば、反応によってエネルギー準位の間隔が大きく変化すると、ボルツマンの式よりエントロピーが大きく変化するので、平衡がどちらに偏るかはエントロピーによる影響を大きく受けることになります。
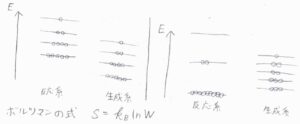
また、分子数の変化もエントロピーを変化させる要因になります。
化学結合が形成されると、動きが拘束される原子数が増加するため、エントロピーは減少することになります。
例として、アンモニアの合成反応について、\(25^\circ \rm{C}\)\(\)、\(10^5\ \rm{Pa}\)\(\)における平衡定数について考えてみましょう。
分子の数は、4つから2つへ減少しますので、エントロピーを減少させる要因となります。
実際の値は、反応エンタルピーが\(-92.2\rm{\ kJ\ mol}\)\(^{-1}\)、反応エントロピーは\(-198.8\rm{\ J\ K}\)\(^{-1}\ \rm{mol}\)\(^{-1}\)となります。
反応エンタルピーは結合の形成と解離によるエネルギーの収支で考えられ、ここでは負の値なので発熱反応になります。
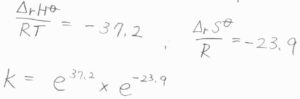
これらの値から平衡定数を考えると、エンタルピー由来の成分は\(e^{37.2}\)、エントロピー由来の成分は\(e^{-23.9}\)となります。
平衡定数は大きい値であるほど、生成系へ平衡が偏ることになりますから、エンタルピーは生成系へ反応を進める方向へ寄与します。
しかし、それをエントロピーが阻害しているため、反応はほとんど進行しないということになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
