こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(flux)
それでは内容に入っていきます!
流束、流束密度
まず、流束というものを考えます。
これは、単位時間あたりに移動する量のことで、分子の数やエネルギー、運動量、電荷などについて考えることができます。
また、流れる管の断面積に比例して流束が大きくなることを考えて、単位面積当たりの流束としたものを流束密度と言います。
流束密度のことを単純に流束と言うことも多く、この記事でも以後、流束密度のことを流束と呼ぶことにします。
流束の例として、金属の棒の一端を加熱した状態をイメージしていただきたいのですが、そのときの熱エネルギーの流束\(J\)は、\(\displaystyle \frac{\Delta E}{A\Delta t}\)と表されます。
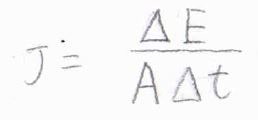
ここで、\(\Delta E\)は正味のエネルギー変化量、\(A\)は棒の断面積、\(t\)は時刻です。
物質輸送
そして、\(z\)軸方向へ拡散している分子については、拡散流束が濃度勾配に比例するという法則が見出されています。
これをフィックの第一法則といいます。
例えば、物質輸送についての流束は、\(\displaystyle -D\frac{\rm{d}\mathit{N}}{\rm{d}\mathit{z}}\)となります。
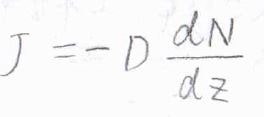
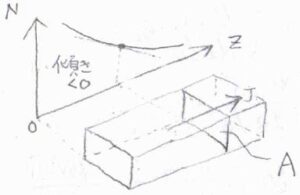
ここで、\(N\)は分子の数密度、\(z\)が拡散運動の方向で、\(D\)は比例定数で、拡散係数と呼ばれます。
濃度が高いところから低いところへ分子は移動するため、マイナスの符号が付きます。
熱伝導
同様に、熱運動する理想的な流体分子について、その熱エネルギー流束は、\(\displaystyle -\kappa \frac{\rm{d}\mathit{T}}{\rm{d}\mathit{z}}\)と書けます。
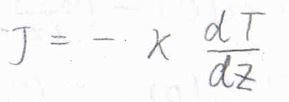
\(T\)は絶対温度で、比例定数の\(\kappa\)は熱伝導率と呼ばれます。
熱運動のエネルギーが絶対温度に比例することから、このような式の形になっています。
ニュートン流動
また、速度勾配が生じたニュートン流体中における速度や運動量の流束も同様に書くことができます。
ニュートン流体とは、せん断応力がずり速度に比例する流体のことです。
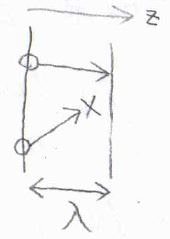
こちらの図のように、\(x\)軸方向への速度\(v_x\)が等しいいくつかの層を考えると、容器の壁に接した層は定常状態であり、壁から離れていくに従って速度は連続的に変化していきます。
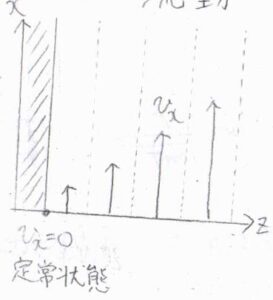
層と層の間では、\(x\)軸方向への運動量のやり取りが行われ、速い層による加速と遅い層による減速が起こるとすると、運動量の流束は\(\displaystyle -\eta \frac{\rm{d}\mathit{v_x}}{\rm{d}\mathit{z}}\)となります。
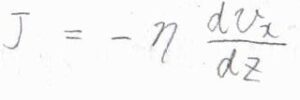
比例定数\(\eta\)は、粘性率もしくは粘度と呼ばれます。
流出(浸出)
ここで補足として、厳密には輸送と異なる概念なのですが、拡散と密接な関係がある流出という現象についても、少しお話しします。
流出とは、この図のように、多孔質膜の小さな穴を通って、物質が散逸する現象のことで、浸出とも言います。
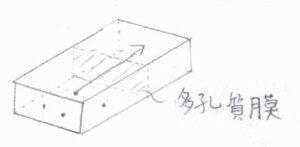
流出する速度\(v\)は、モル質量\(M\)の平方根に反比例することが経験則として1840年代には知られており、これをグレアムの法則と言います。
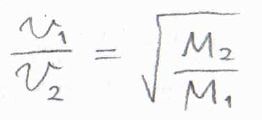
そのあとに、気体分子運動論によって、理論的にも正しいことが確かめられました。
放射性同位体を拡散によって分離するときの基礎として、原子爆弾の開発にも利用されました。
衝突流束
ここからは、ボルツマン分布に従う理想気体の分子について、流束や流出速度がどのような依存性をもつのかを考えていきます。
速度分布として、一次元のマクスウェル-ボルツマン分布の式を使います。
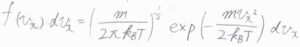
\(k_\rm{B}\)はボルツマン定数、\(m\)は分子の質量です。
導出過程は、こちらを参照してください。
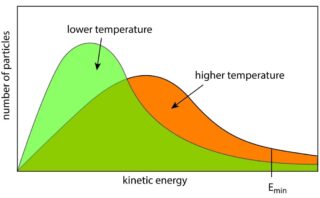
気体分子運動論で壁との衝突頻度を考えたのと同様に、衝突の流束、すなわち単位時間・単位面積あたりのある仮想的な窓への衝突回数を考えます。
これを\(Z_\rm{w}\)とすると、これは数密度\(N\)と壁に向かう速さの期待値の積として書けます。
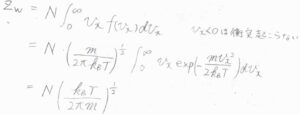
壁から離れていく方向へと運動している分子は衝突が起こりえないので、積分の範囲は\(v_x\)が正のときのみを考えています。
ガウス積分の公式より、\(Z_\rm{w}\)\(\displaystyle =N\sqrt{\frac{k_\rm{B}\mathit{T}}{2\pi m}}\)となります。
理想気体の状態方程式\(pV=nRT\)より、数密度\(\displaystyle N=\frac{p}{k_\rm{B}\mathit{T}}\)と書けるので、\(Z_\rm{w}\)\(\displaystyle =\frac{p}{\sqrt{2\pi mk_\rm{B}\mathit{T}}}\)となります。
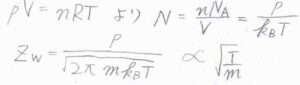
体積が一定のとき、圧力は温度に比例するため、衝突流束\(Z_\rm{w}\)は、\(\displaystyle \sqrt{\frac{T}{m}}\)に比例するということになります。
また、三次元的な並進運動の速さの平均\(\displaystyle \bar{v}=\sqrt{\frac{8k_\rm{B}\mathit{T}}{\pi m}}\)であることと照らし合わせると、\(\displaystyle \bar{v}=\frac{4Z_\rm{w}}{N}\)という関係式も得られます。
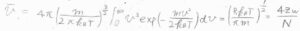
この衝突流束と、気体分子運動論からくる平均自由行程を利用すると、拡散係数など前半で紹介した流束の比例定数の各種パラメータに対する依存性を理解することができます。
拡散係数
順番に、まずは拡散係数について考えていきます。
始めに、\(z\)軸方向へと移動する分子の濃度勾配がこちらのグラフのように表されたとします。

そして、ある時刻に\(z=0\)の地点にある分子は、その直前に平均自由行程\(\lambda\)だけ離れた地点でほかの分子と衝突していたと考えます。
正の方向と負の方向の衝突流束の差が、正味の物質流束\(J_z\)となるため、\(z=\pm \lambda\)における分子の数密度が一次の項までで近似できるとき、\(\displaystyle J_z=-\frac{1}{2}\bar{v}\lambda (\frac{\rm{d}\mathit{N}}{\rm{d}\mathit{z}})_0\)となります。
ただ、厳密には\(z\)軸に平行ではない方向への拡散(平均自由行程より長いと、実際はその前に衝突が生じるため、ほとんど起こらない)も数えられていることで、流束を過大評価しているため、この式は正しくありません。
現実と照らし合わせるときには、\(\displaystyle J_z=-\frac{1}{3}\bar{v}\lambda (\frac{\rm{d}\mathit{N}}{\rm{d}\mathit{z}})_0\)という修正した式が用いられることになります。
(下の式は三次元格子モデルの式で、\(\displaystyle \frac{1}{6}\)は上下左右前後のうち1方向だけが衝突に関与することに由来する。より詳細な議論や現実も、このモデルの結果に一致する。)

\(\displaystyle (\frac{\rm{d}\mathit{N}}{\rm{d}\mathit{z}})_0\)の前にある\(\displaystyle \frac{1}{3}\bar{v}\lambda\)が拡散係数\(D\)に相当します。
分子の形状を球としたとき、理想気体分子の拡散係数は、分子の直径\(d\)の二乗に反比例します。
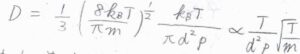
圧力が大きいほど平均自由行程は短くなるため、拡散係数も圧力に反比例して小さくなります。
圧力は温度に比例するため、分子にある\(T\)はキャンセルされて、拡散係数は絶対温度の平方根に比例し、分子の質量の平方根には反比例するということになります。
熱伝導率
続いて、同様の操作をエネルギー流束について行うと、次のようになります。
ここでは、分子1個がもつ熱運動のエネルギーがすべて等しく、等分配則より\(\nu k_\rm{B}\)\(T\)と書けるものと考えます。
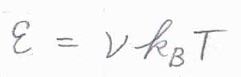
そして、\(z=\pm \lambda\)のときのエネルギーを一次の項まで考えると、エネルギー流束\(\displaystyle J_z=-\frac{1}{3}\nu\bar{v}\lambda Nk_\rm{B}\)\(\displaystyle (\frac{\rm{d}\mathit{T}}{\rm{d}\mathit{z}})_0\)となります。
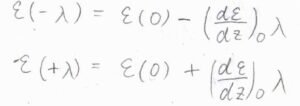
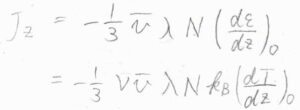
したがって、熱伝導率\(\displaystyle \kappa=\frac{1}{3}\nu\bar{v}\lambda Nk_\rm{B}\)となります。

アボガドロ定数を\(N_\rm{A}\)、モル濃度を\([\rm{J}]\)とすると、数密度\(N=N_\rm{A}\)\([\rm{J}]\)であり、さらに、定積モル熱容量\(C_{V, \rm{m}}\)が\(\nu k_\rm{B}\)\(N_\rm{A}\)と表されることを利用すると、\(\displaystyle \kappa=-\frac{1}{3}\bar{v}\lambda C_{V, \rm{m}}[\rm{J}]\)と変形することもできます。
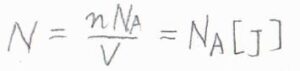
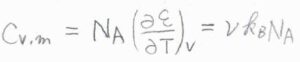
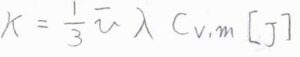
さらに、\(\displaystyle \frac{1}{3}\bar{v}\lambda\)は拡散係数\(D\)と書くこともできます。
また、拡散係数の式と、理想気体の状態方程式を使うと、\(\displaystyle \kappa=\frac{\nu pD}{T}\)という形にもできます。
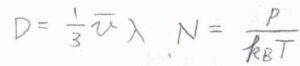
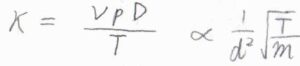
この式は、まず分子が大きくなるにつれて拡散しにくくなるのに伴い、熱伝導も遅くなることを示しています。
また、熱伝導率は圧力に依存しないことも示しています。
これは、濃度増加によってエネルギーの運び手が多くなる効果と、衝突頻度が大きくなりエネルギー輸送が妨げられる効果がつりあうことが理由になっています。
実験的にも、圧力が大きいときには熱伝導率に圧力依存性が現れないことが確かめられています。
ただし、圧力がとても小さいときには、熱伝導率が圧力に比例することが知られています。
これは分子の平均自由行程が長くなりすぎて、エネルギーの輸送距離が容器の大きさだけで決まるようになることで生じる挙動です。
粘性率
ニュートン流動についても同様に考えると、粘性率\(\displaystyle \eta=\frac{1}{3}\bar{v}\lambda mN\)となります。
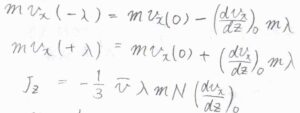
モル質量\(M\)とモル濃度\([\rm{J}]\)を使うと、\(MD[\rm{J}]\)と変形できます。
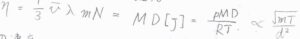
運動量が質量と速度の積であることから、粘性率は質量の平方根に比例することになります。
流出速度
最後に、流出速度\(v\)について考えます。
多孔質隔壁の穴の総面積を\(A\)とすると、衝突流束を使って、\(v=Az_\rm{w}\)と書けます。
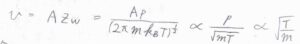
したがって、\(\displaystyle v=\frac{Ap}{\sqrt{2\pi mk_\rm{B}\mathit{T}}}\)となり、この結果はグレアムの法則と一致します。
圧力が温度に比例するため、流出速度は絶対温度の平方根に比例します。
固体と液体の蒸気圧がとても小さいとき、その質量減少から流出速度を計算することで、蒸気圧を決定するクヌーセン法という蒸気圧決定手法は、この流出速度の式がクヌーセン法の理論的な基礎になっています。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!