こんにちは!
それでは今回も化学のお話やっていきます。
今日から熱力学の話もやっていきます。
今回はテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Maxwell-Boltzmann)
それでは内容に入っていきます!
ボルツマン分布
まず、今回考えるモデルを紹介します。
密封された容器の中に理想気体分子が5個あるとします。
体積は\(V\)で一定、この分子は5つの離散的なエネルギー状態をとります。
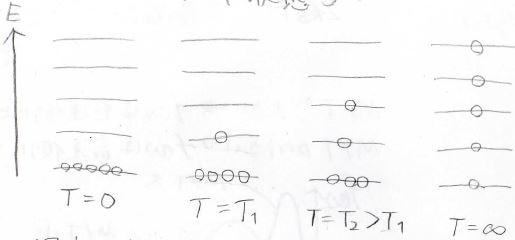
それぞれの分子がどのエネルギー状態にあるのかは温度によって変わります。
絶対零度のときにはすべての分子が最安定の状態にありますが、温度の上昇とともに高いエネルギー状態に移っていきます。
しかし、最安定の状態にまったく分子がいないという状態にはなりにくくて、とても高い温度になった場合にはすべての状態で分子の存在確率が近い値になっていきます。
この分子がどのエネルギー状態に平均で何個入るのかという分布には法則があり、このような式で表されます。


\(i\)と\(j\)が状態の番号で、\(N\)が分子の個数です。
この式の意味は\(i\)番目と\(j\)番目の分子数の比は、状態間のエネルギー差と温度で決まるということです。
温度が低いほど、またエネルギー差が多いほど安定な状態に分子が集中することになります。
この分布をボルツマン分布と言います。
エネルギー状態が縮退しているときには、縮退度\(g\)を使って、下のように考えます。
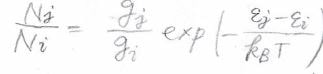
なぜ指数関数になるのかは、こちらを参照してください。

マクスウェル-ボルツマン分布の導出
では、今回のテーマであるマクスウェル-ボルツマン分布を先ほどのボルツマン分布から導いてみましょう。
ボルツマン分布は分子数の分布でしたが、このマクスウェル-ボルツマン分布は速度の分布です。
分子はすべてが同じ速さで運動しているわけではないので、どのような広がりを持っているのかを考えます。
ここでは先ほどのように離散的なエネルギーではなく、連続量である並進エネルギーを分子がもつ全エネルギーとします。
そして、速度ベクトルを\(\boldsymbol{v}=(v_x, v_y, v_z)\)、その絶対値を\(v\)と置きます。
分子がもつ並進エネルギーは\(\displaystyle \frac{1}{2}mv^2\)となって\(x\)、\(y\)、\(z\)成分に分離することもできます。
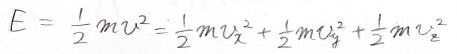
ここで\(x\)成分にのみ考えることにすると、\(v_x\)の分布関数\(f_x\)はこのような式になります。

指数関数の部分はボルツマン分布からきており、これに規格化定数\(\displaystyle K\)をかけた形になっています。
この\(K\)はガウス積分の公式より求めることができて、\(\displaystyle \sqrt{\frac{m}{2\pi k_\rm{B}\mathit{T}}}\)になります。
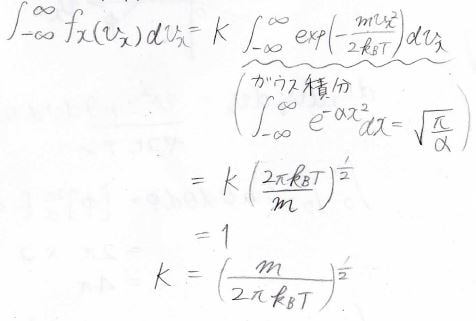
次に、\(x\)方向についてはわかったので、ここから全方向を考えます。
全体の速度分布関数\(f\)は、\(x\)、\(y\)、\(z\)すべての軸方向に対する分布関数の積になるため、下のように書けます。

また分子の並進運動は等方的であり、偏りはないため、\(v_x\)の分布関数\(f_x\)と同じ形で、\(f_y\)、\(f_z\)も書くことができます。
すでに規格化定数は求めたので、結局全方向への速度分布は上の形になります。
そして、角度依存性がないということは、極座標にすると変数を速度\(v\)だけにできるということなので、ここから極座標への変換を行います。
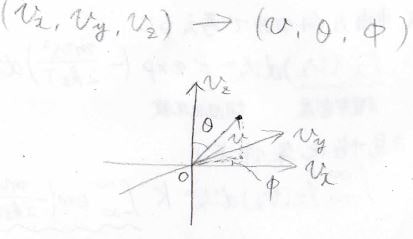
ヤコビアンは\(v^2\sin{\theta}\)で、微小な体積変化は下のように書けます。
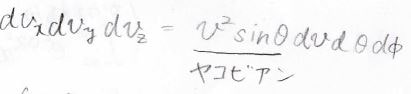
ここの考え方について、詳しくは別の記事でお話ししているので、必要に応じてこちらを参照してください。

そして、この角度部分を積分すると\(4\pi\)になります。
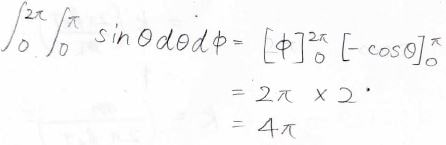
結局、極座標で表したときの速度分布は、下の式になります。

この分布をマクスウェル-ボルツマン分布と言います。
モル質量を\(M\)、気体定数を\(R\)とすれば、指数関数の部分をこのように変形することができます。
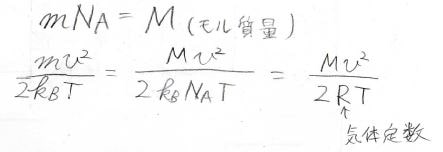
温度依存性、モル質量依存性
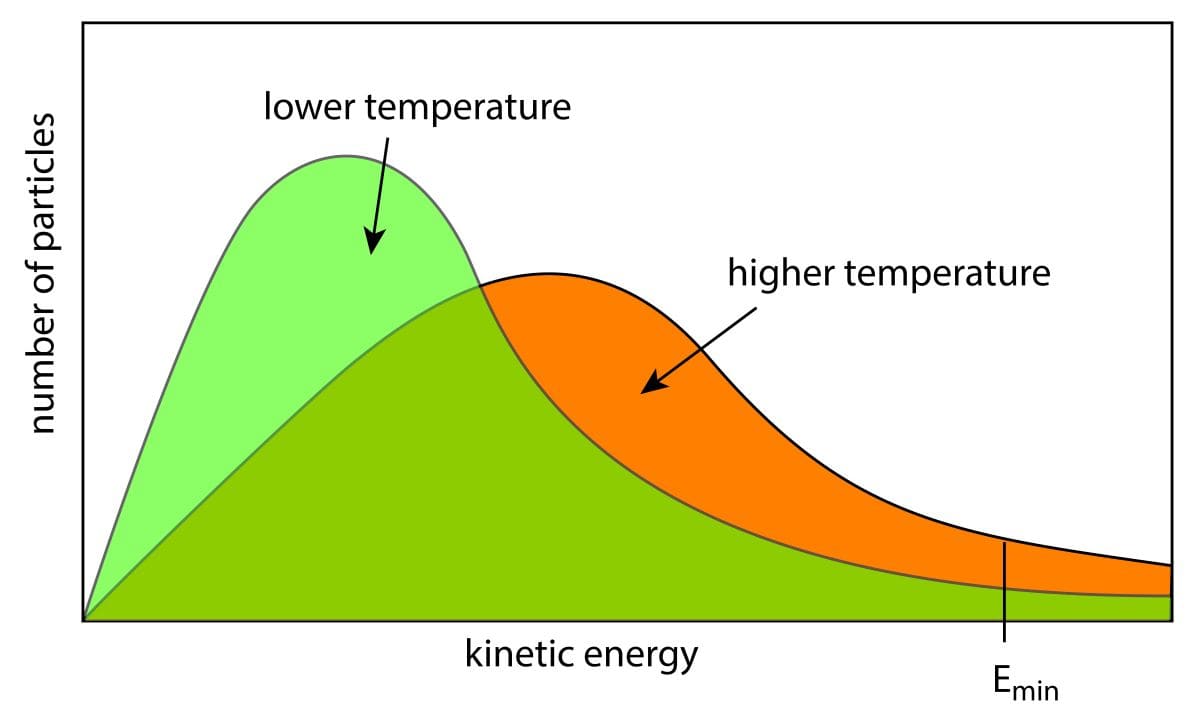
ここで、速度分布が何に依存するのかを考えてみます。
\(v\)は変数で、\(R\)は物質や条件によらない定数なので、モル質量\(M\)と絶対温度\(T\)によってこの関数の形が変わることになります。
もっと言うと、理想気体の場合は分子の大きさもないので、この\(M\)と\(T\)の比によって変わることになります。
つまり個々の値は問題ではなく、温度が下がることは分子量が大きくなることと対応しています。
もし、\(\displaystyle \frac{M}{T}\)が大きいときには低速側にピーク、\(\displaystyle \frac{M}{T}\)が小さいときには高速側にピークが現れます。
図で書くとこんな感じで、青は\(\displaystyle \frac{M}{T}\)が大きいとき、すなわちモル質量が大きいか、低温だった場合の速度分布です。
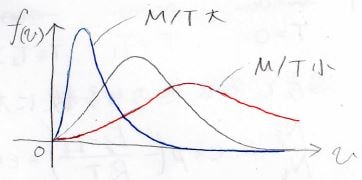
赤はその逆です。
ここでもう1つ注目してもらいたいのは、ピークの幅です。
青のカーブは分布が狭く、速い分子はほとんど存在していないことになります。
それに対して、赤のカーブはブロードになっており、遅い分子もそこそこ存在していることになります。
これは、ボルツマン分布においてどんなに高い温度にしても、最安定状態に分子がいることからイメージしてもらえると思います。
ずべての分子が一様の速さをもっているわけではないことは、反応速度を考えるうえでもとても重要な事実です。
詳しくは、こちらを参照してください。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!