こんにちは！
それでは今回も化学のお話をしていきます。
今回のテーマはこちらです！
動画はこちら↓
動画で使ったシートはこちら(Schrodinger equation)
複素数の波
まず復習ですが、先日の記事で、波であれば普遍的に満たす波動方程式の導出と、複素数の領域に拡張した一般的な波は\(\exp[\rm{i}(\mathit{kx-\omega t})]\)で与えられることをお話ししました。
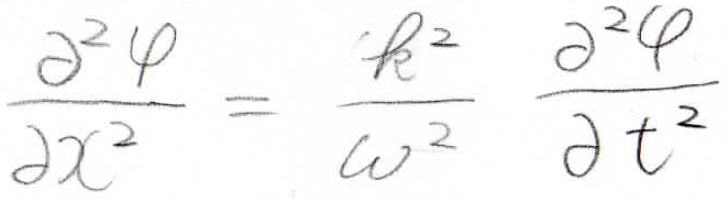
詳しく知りたい方はこちらからチェックしてください。
量子の二重性
ここから、量子がもつ性質を考慮していきます。
量子の一番特徴的な性質は何かというと、粒子でありながら波でもあるということです。
例えば、電子は蛍光灯の中で水銀原子と衝突して紫外線を放出しています。
この衝突は、電子が粒子であるがゆえに起こることです。
この現象についてはこちらで詳しく説明しています。
しかし、1974年にミラノ大学で行われた実験では1個の電子でも二重スリットを通過して、干渉縞を作ることが証明されました。
電子は自らと干渉したということです。
つまり、電子は粒子でありながら波の性質も持っていたということになります。
量子のこの性質は二重性と呼ばれます。
ちなみに普段、波として見えている光も粒子としての性質を持っています。
これは高校でも習う光電効果で説明されています。
シュレディンガー方程式の導出
量子がもつ波長はド・ブロイ波長の式で求められ、\(h/p\)になります。
\(p\)は運動量で、\(h\)はプランク定数(\(=6.626\times 10^{-34}\ \mathrm{J\ s}\))です。
光電効果より、量子がもつ運動エネルギーは振動数に比例することがわかっています。
その比例定数がプランク定数\(h\)です。
それではこの2つの式を使って、角波数\(k\)と角周波数\(\omega\)を変形していきましょう。
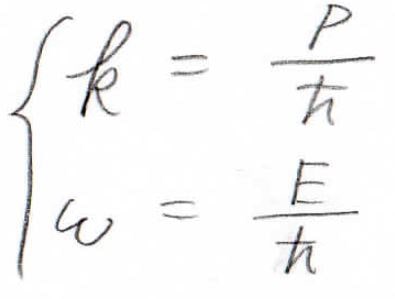
ここで、\(h/2\pi\)を\(\hbar\)と書き換えることにします。
この\(\hbar\)は換算プランク定数またはディラック定数と呼ばれますが、そのままエイチバーと呼ぶことが多いです。
\(\hbar\)を使うと、\(k=p/\hbar\)、\(\omega=E/\hbar\)となって、簡素な形になります。
それで、今度は運動エネルギー\(E\)が\(p^2/2m\)で与えられることを利用します。
すると\(\omega =p^2/2m\hbar\)となります。
\(p^2\)を\(k\)で表したものを代入して整理すると最終的には\(\omega =(\hbar/2m)k^2\)となります。
この式を使って元の波の\(t\)についての偏微分を考えてみると、下のようになります。
時間についての一階偏微分と空間についての二階偏微分が結びつくという面白い式です。
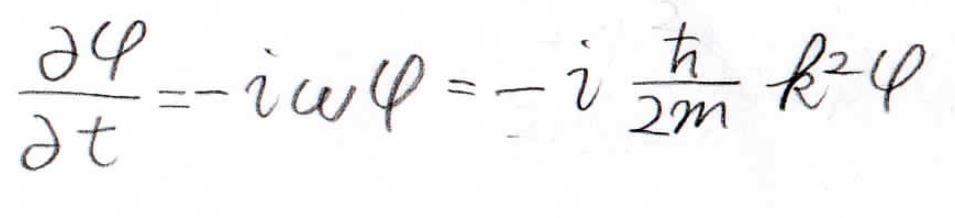
ここから少し強引ですが、この\(t\)についての偏微分に\(\rm{i}\)\(\hbar\)をかけてみます。
すると、右辺に運動エネルギーが現れます。
このことから、\(\rm{i}\)\(\hbar \frac{\partial }{\partial t}\)という演算子は、スカラー量のエネルギーに相当すると考えることができます。
このとき、\(\rm{i}\)\(\hbar \frac{\partial }{\partial t}\)はエネルギー演算子であるといいます。
\(\hat{E}\)と表記してイーハットと呼びます。
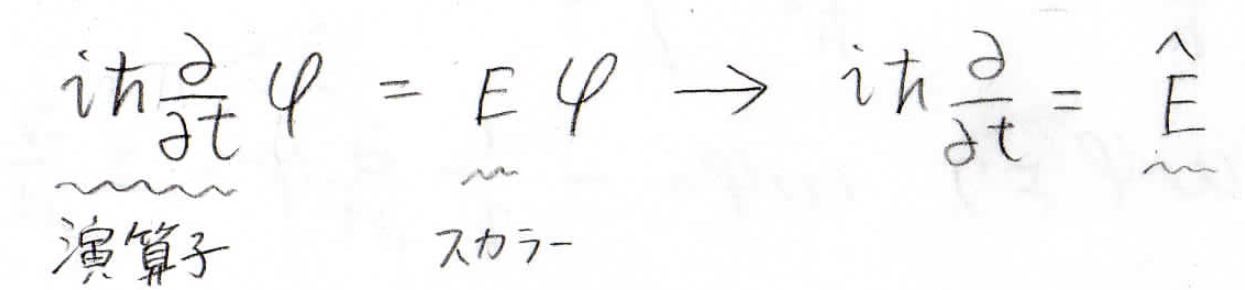
また、エネルギー演算子は\(\hat{p}^2/2m\)と考えることができるので、\(-\hbar ^2\frac{\partial ^2}{\partial x^2}\)は運動量演算子の2乗となります。
このことから、運動量演算子は\(\rm{i}\)\(\hbar \frac{\partial }{\partial x}\)であることがわかります。
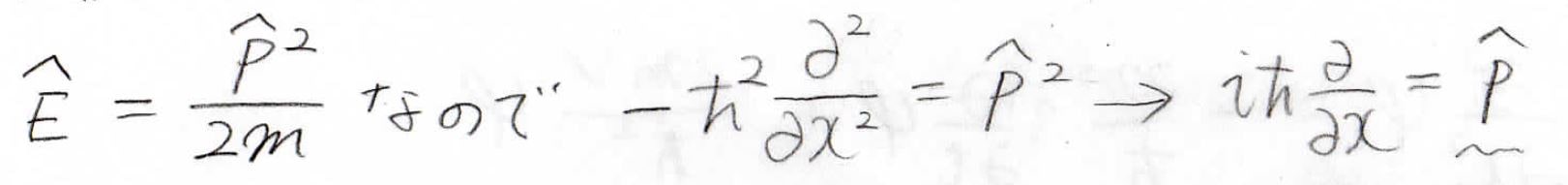
そして、ここまではポテンシャルエネルギー(高校では位置エネルギー)を考慮せずに変形していましたが、運動エネルギーとポテンシャルエネルギー\(V(x)\)の和である力学的エネルギーを考えると、下のようになります。
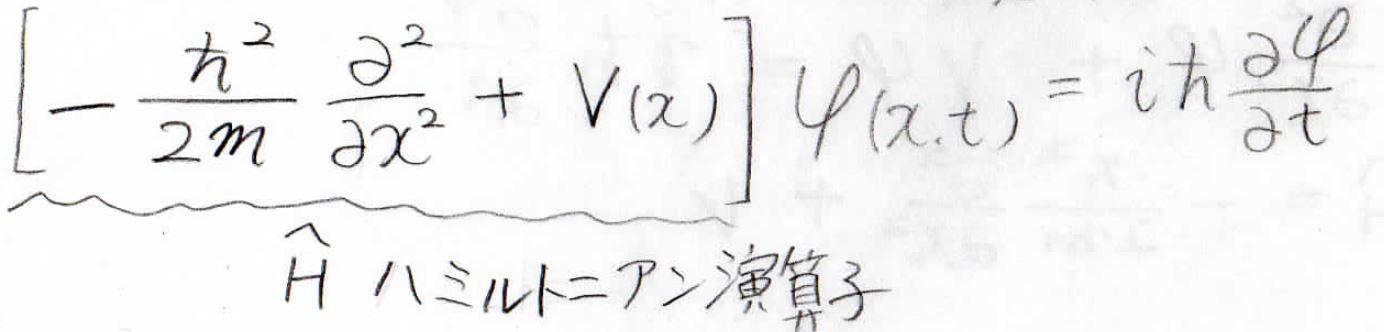
この式こそがシュレディンガー方程式で、量子力学の基本的な式になります。
古典力学におけるニュートンの運動方程式みたいなものだと思ってください。
左辺の\([]\)で囲んだ部分は全エネルギーを導くための演算子であり、ハミルトニアン演算子と呼ばれます。
文字であらわすときは\(\hat{H}\)と書きます。
時間依存しない形のシュレディンガー方程式
そして、このシュレディンガー方程式を解く際には、もう少し変形した形で扱うことが多いので、練習問題の前にそれも紹介しておきます。
まず、\(\exp[\rm{i}(\mathit{kx-\omega t})]\)という波を下のように、変数ごとに分けたのちに、\(A\exp(\rm{i}\mathit{kx})\)の部分を\(\phi (x)\)とします。
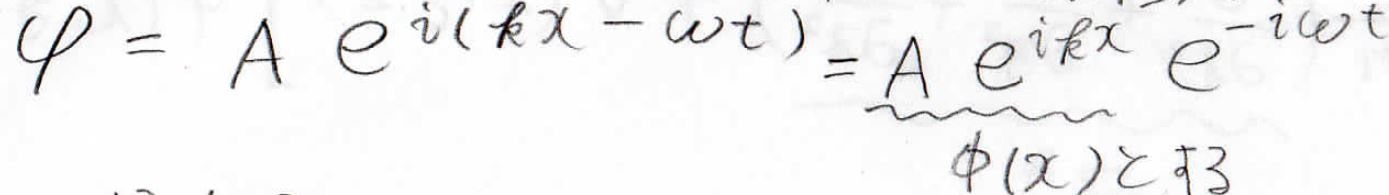
そして、シュレディンガー方程式に入れてみると、すべての項に\(\exp(-\rm{i}\mathit{\omega t})\)がかかっているので、両辺をこれで割ると、変数を\(x\)だけにすることができ、微分方程式として解くのが簡単になります。
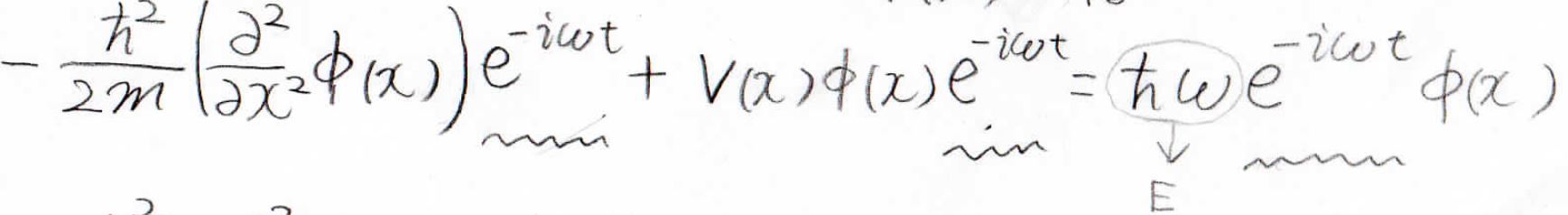
また、右辺の\(\hbar \omega \)はエネルギー\(E\)なので、最終的にこちらの形になります。
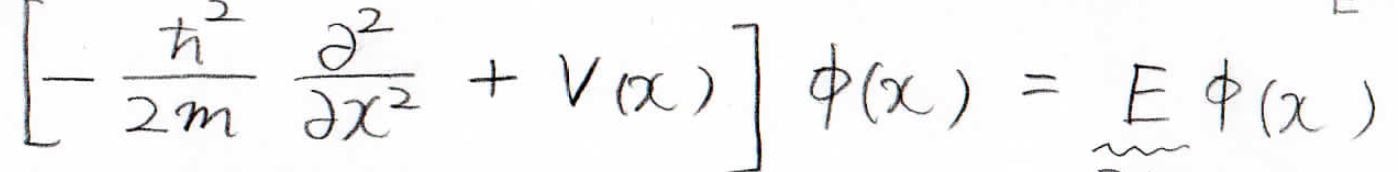
時間依存しない形にして変わったことは、エネルギー演算子\(\hat{E}\)が物理量であるエネルギー\(E\)に変わっていることです。
微分方程式についてはこちらで解説しています。
このシュレディンガー方程式を使えば、原子中の電子がどのように存在しているかなどが計算できるというわけです。
三次元、時間依存しない形のシュレディンガー方程式
最後、量子力学で電子の状態を考える場合、三次元空間で考えるのが自然なので、その形も紹介しておきます。
三次元のときは、このように\(\boldsymbol{\nabla}\)が入った形のシュレディンガー方程式になるので、知っておいてください。
練習問題
といったところでいつも通り練習問題です。
先ほど、ポテンシャルエネルギーを考慮しない系から考慮した系にしたときに、\(V(x)\)を式に入れましたが、本当にそうなるのかをまだ確かめていません。
そこで、\(E=p^2/2m+V\)とおいて、ハミルトニアンが\(-\frac{\hbar ^2}{2m} \frac{\partial ^2}{\partial x^2}+V\)と書けるかどうかを確かめてくださいというのが問題です。
こんな感じで、最終的にはハミルトニアンに\(+V\)が現れます。
まとめ
それではまとめに入ります。
おさらいをしておくと、まずシュレディンガー方程式は、複素数の波に量子の二重性を考慮することで導かれました。
運動量演算子は\(\rm{i}\)\(\hbar \frac{\partial }{\partial x}\)で、ハミルトニアンは\(-\frac{\hbar ^2}{2m} \frac{\partial ^2}{\partial x^2}+V\)です。
ということで、今回の内容は以上です。
どうもありがとうございました！
