こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(miller index)
それでは内容に入っていきます!
結晶と単位胞
そもそも結晶とは、分子や原子、イオンが三次元的に規則正しく配列してできている固体のことです。
結晶構造の最小となる集団のことは単位胞と呼ばれ、並進を伴う複製を繰り返すことで、結晶全体の構造を作ることができます。
単位胞の構造を理解することは、結晶全体の機械的、電気的、光学的な性質などを理解するうえで非常に重要です。
二次元の空間格子を例にすると、こちらの図の中で色で囲まれたものが単位胞にあたります。

空間格子とは、結晶構造の規則性を数学的に表現するために導入された点の集合のことを言言います。
単位胞は隙間なく並べられる形をしている必要があるため、円や正五角形は単位胞になりえません。
ただ、平行四辺形であれば、必ずしも正方形である必要はなく、図のようにさまざまな形の単位胞を考えることができます。
そして、三次元の単位胞といえば、通常、その辺が最も短く、面同士が垂直に近い角度で交わるような平行六面体を選びます。
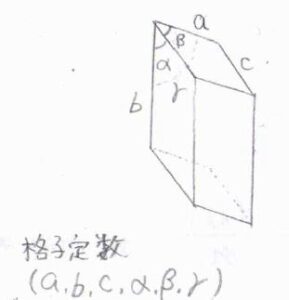
単位胞の構造は、3辺の長さ\(a\)、\(b\)、\(c\)と3つの角度\(\alpha\)、\(\beta\)、\(\gamma\)という6つのパラメータを使うことで表すことができ、これらの値は格子定数と呼ばれます。
隣接する格子点を結んでできる単位胞は単純単位胞、面や中心に格子点を含む単位胞は非単純単位胞と言言います。
結晶構造の分類
結晶系
続いて、単位胞をその回転対称性から分類した結晶系というものについて、お話しします。
分子について対称操作を考えたときと同様に、ある軸を中心として回転させても、元の形の単位胞と重なることがあります。
どの回転対称性をもつかにより、単位胞は7つに分類されます。
単位胞がその結晶系に属するために必須となる対称要素とその名称は、こちらの表のとおりです。

例えば、3辺の長さがすべて異なり、3つの角度もすべて異なる場合は、回転軸をもたず、三斜単位胞に分類されます。
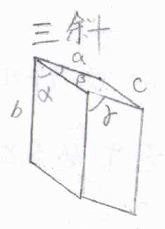
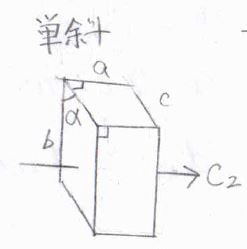
3つのうち2つの角度が\(90^\circ\)で、3辺の長さが異なる場合、2回回転軸を1つもつことになり、これを単斜単位胞と言言います。
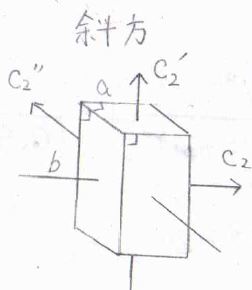
3つの角度がすべて\(90^\circ\)のときには、3本の2回回転軸をもつことになり、これを斜方単位胞と言言います。
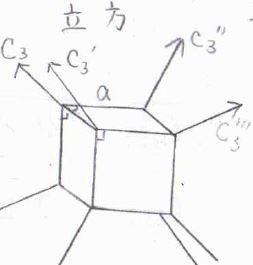
さらに3辺もすべて同じ長さのときには、この図のように4本の3回回転軸が存在することになり、これを立方単位胞と言言います。
ブラべ格子
以上が回転対称性によって分類した結晶系でしたが、ここまでの話だと、単純単位胞と非単純単位胞が区別できていません。
実は、三次元において可能な空間格子は14個しかないことが知られており、それを分類したものはブラべ格子とい言います。
格子点の配置に対応する大文字のアルファベットを結晶系の後につけることで、ブラベ格子は記述されます。

\(\rm{P}\)は単純単位胞、\(\rm{F}\)は面心単位胞、\(\rm{I}\)は体心単位胞、\(\rm{R}\)は菱面体単位胞、\(\rm{C}\)(または\(\rm{A}\)か\(\rm{B}\))は底心単位胞を指します。
14種類のブラべ格子は、こちらの表に示したとおりです。
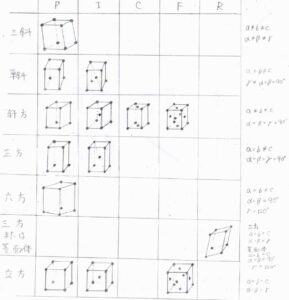
黒丸は、格子点を指します。
一番右には、格子定数の条件を書いて言いますが、\(a\neq b\neq c\)は、3辺の長さがすべて異なるということを意味していると思ってください。
この表の注意点ですが、黒丸で示した格子点の位置が原子や分子の中心と一致するのは、必須事項ではありません。
空間格子はあくまで点の集合に過ぎず、ブラべ格子の単位胞内にある等価な格子点は、すべて同じ周辺構造をもちます。
格子点となる位置に原子中心がなかったとしても、その結晶に対応する単位胞であることに変わりありません。
格子面とミラー指数
続いて、結晶格子内を通る平面をどのように表すのかを考えます。
これから説明する表記の方法は、結晶にX線を当てたときに、どの面で光の回折が起こったのかを文献等で表すために利用されます。
ここでは、すべての角が\(90^\circ\)で、3辺の長さが異なる斜方格子を例に考えていきます。
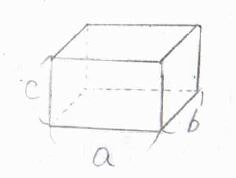
まず、こちらの図のように、格子内を平面が通るとしましょう。
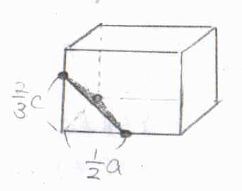
ラベルを付けることでこの面を指定したいとき、3つの点の座標が必要になります。
そこで、結晶格子の頂点の1つを原点として、三次元の直交座標を考えます。
これを結晶座標とい言います。
3点の座標は、\(\displaystyle (\frac{1}{2}a, 0, 0)\)と\(\displaystyle (0, b, 0)\)と\(\displaystyle (0, 0, \frac{2}{3}c)\)であるため、これを文献に書けば、どの面を指しているのかが一応伝わります。
ただ、切片の座標で指定する前提なら、\(0\)を書かなくてもわかるので、\(\displaystyle (\frac{1}{2}, 1, \frac{2}{3})\)と表記しても、特定の面を指定することができます。
同様に、こちらの図のように、どんな平面にも切片の座標を使ってラベルを付けることができます。
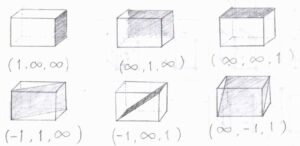
格子のいずれかの辺と平行な面の場合は、切片が無限大であるとして考えます。
隣り合った格子を考えれば、切片が負の値となるような面も考えることができます。
そして、これから紹介するミラー指数を使えば、このラベルを簡単な整数の組に直すことができます。
まず、切片座標によるラベルについて、それぞれの逆数をとります。
その際、負の指数には数字の上に横線を引きます。
逆数をとった結果、分数が出てくる場合は、全体を整数倍して、\(1\)以外の公約数をもたない整数の組を作ります。
例えば、切片座標が\((-1, 1, \infty)\)の面をミラー指数で表すと\((\bar{1}\ 1\ 0)\)となります。
\(\displaystyle (2, -1, \frac{1}{2})\)は、\((1\ \bar{2}\ 4)\)となります。
これは表記上の注意ですが、まず\((h\ k\ l)\)面と書くと、格子中を通る1つの面を指します。
その小かっこを中かっこにして、\(\{h\ k\ l\}\)面と書かれている場合には、特定の面ではなく、\((h\ k\ l)\)面に平行なすべての面の組を指すことになるので、覚えておいてください。
格子面の間隔
そして、平行な2つの面の間隔\(d_{hkl}\)とX線の波長との関係によって干渉が起こるのですが、\(d_{hkl}\)は次のように計算することができます。
まず切片座標を\((a’, b’, c’)\)とすると、\(\displaystyle h=\frac{a}{a’}\)、\(\displaystyle k=\frac{b}{b’}\)、\(\displaystyle l=\frac{c}{c’}\)であることから、\(\displaystyle a’=\frac{a}{h}\)、\(\displaystyle b’=\frac{b}{k}\)、\(\displaystyle c’=\frac{c}{l}\)と書けます。
格子の底面にだけ着目すると、図中の角度\(\phi\)について、\(\displaystyle \sin{\phi}=\frac{hd_{hk0}}{a}\)、\(\displaystyle \cos{\phi}=\frac{kd_{hk0}}{b}\)と求められます。
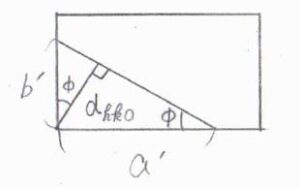
\(\sin^2{\phi}+\cos^2{\phi}=1\)より、\(\displaystyle \frac{1}{d_{hk0}^2}=\frac{h^2}{a^2}+\frac{k^2}{b^2}\)という関係式が得られます。
どの辺の長さを\(a\)、\(b\)、\(c\)とするかによって面の間隔は変化しないはずなので、これを三次元に拡張すれば、\(\displaystyle \frac{1}{d_{hkl}^2}=\frac{h^2}{a^2}+\frac{k^2}{b^2}+\frac{l^2}{c^2}\)となります。
右辺を数値的に計算し、その逆数の平方根をとることで、面の間隔が計算されます。
仮にミラー指数が\(1\)以外の公約数をもつことを許容すると、自然数\(n\)として\(d_{nh, nk, nl}\)も計算可能です。
その結果、\(\displaystyle d_{nh, nk, nl}=\frac{d_{hkl}}{n}\)となるため、ミラー指数を\(n\)倍すると、もとの面と平行なまま、面の間隔が\(\displaystyle \frac{1}{n}\)倍になると言えます。
練習問題
斜方単位胞について、\(a=0.82\ \rm{nm}\)、\(b=0.94\ \rm{nm}\)、\(c=0.75\ \rm{nm}\)のとき、\(d_{132}\)と\(d_{264}\)は、それぞれいくらになるでしょうか?
その逆数の平方根を取れば、\(d_{132}=0.23\ \rm{nm}\)と計算できます。
そして、\(\displaystyle d_{264}=\frac{d_{132}}{2}\)より\(d_{264}=0.12\ \rm{nm}\)と求められます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




