こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(ideal phase diagram)
それでは内容に入っていきます!
2成分系における理想溶液と理想気体の平衡状態
モデル
こちらが今回考えるモデルです。

2成分\(\rm{A}\)と\(\rm{B}\)はともに揮発性であり、液相と気相の両方に存在します。
液相は理想溶液、気相は理想気体です。
したがって、液相については、ラウールの法則が成り立ちます。
ラウールの法則については、こちらを参照ください。

液相中のモル分率は\(x\)、気相中のモル分率は\(y\)という文字で表します。
液相と気相それぞれの組成の関係
気相について、その全圧\(p\)は、\(\rm{A}\)の分圧\(p_\rm{A}\)と\(\rm{B}\)の分圧\(p_B\)の和なので、\(x_\rm{A}\)\(p_\rm{A}\)\(^\ast+x_\rm{B}\)\(p_\rm{B}\)\(^\ast\)となります。
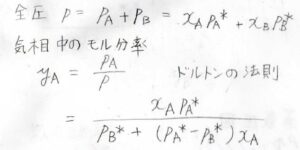
また、気相は理想気体であることより、ドルトンの法則から\(y_\rm{A}\)\(\displaystyle =\frac{p_\rm{A}}{p}\)となります。
したがって、\(y_\rm{A}\)\(\displaystyle =\frac{x_\rm{A}\mathit{p}_A^\ast}{p_\rm{B}^\ast+(\mathit{p}_A^\ast-\mathit{p}_B^\ast)\mathit{x}_A}\)となります。
これが液相の組成と気相の組成の関係です。
\(\rm{B}\)よりも\(\rm{A}\)の方が揮発性が高いとき、つまり\(p_\rm{A}\)\(^\ast \gt p_\rm{B}\)\(^\ast\)のときには、このグラフのようにあらゆる組成において\(y_\rm{A}\)\( \gt x_\rm{A}\)となります。

なお、グラフに書かれた値は、\(\frac{p_\rm{A}^\ast}{p_\rm{B}^\ast}\)を表しています。
液相と気相の組成は、一般的に一致しません。
気相では、揮発性が高い成分のモル分率が大きくなります。
それぞれの成分の飽和蒸気圧が等しい場合のみ、液相と気相の組成が一致することになります。
そして、先ほど求めた\(y_\rm{A}\)と\(x_\rm{A}\)の関係式を、\(x_\rm{A}\)について整理すると、\(x_\rm{A}\)\(=\displaystyle \frac{y_\rm{A}\mathit{p}_B^\ast}{p_\rm{A}^\ast+(\mathit{p}_B^\ast-\mathit{p}_A^\ast)\mathit{y}_\rm{A}}\)となります。
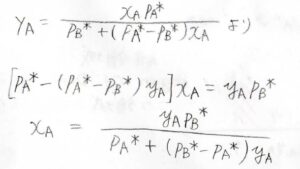
\(x_\rm{B}\)も\(1-x_\rm{A}\)として、このように表されます。
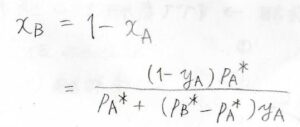
蒸気圧図
これを代入すれば、全圧\(p\)と気相中の\(\rm{A}\)のモル分率\(y_\rm{A}\)の関係を導くことができます。
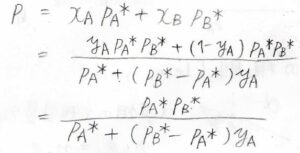
\(\displaystyle p=\frac{p_\rm{A}^\ast \mathit{p}_B^\ast}{p_\rm{A}^\ast+(\mathit{p}_B^\ast-\mathit{p}_A^\ast)\mathit{y}_A}\)となります。
これをグラフにすると、このような曲線が書けます。
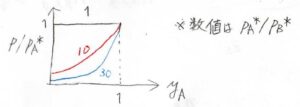
反比例のグラフを平行移動したものです。
横軸が\(y_\rm{A}\)、縦軸が\(\displaystyle \frac{p}{p_\rm{A}^\ast}\)です。
\(\rm{A}\)の揮発性が高いほど、全圧に占める\(\rm{A}\)の分圧が大きくなります。
液相については、ラウールの法則が成り立つので、全圧はモル分率の一次関数であり、グラフは直線になります。
縦軸を全圧、横軸をそれぞれのモル分率として、1つのグラフにすると、下のようになります。

このように、全圧と組成の関係を表した図を蒸気圧図と呼びます。
上側が液相で、下側が気相になります。
そして、もうひとつ液相の直線と気相と曲線に囲まれた領域が存在します。
この領域は、相分離領域、略してRODと呼ばれるもので、この領域の圧力と組成は、どちらの相にも存在しないことになります。
状態変化の過程
RODが存在するとき、液相の1相状態から気相1相状態までの変化の過程は、下のようになります。
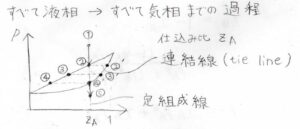
\(z_\rm{A}\)は仕込み比と言って、液相と気相を合わせた全体の組成を表します。
まず、液相の点①から減圧していくと、仕込み比の組成を保ちながら直線状の点②に到達します。
ここから下の領域には、液相は存在できないので、一部が気相へ移ります。
そのとき、気相の組成は、曲線上で点②と同じ全圧となる点②’となります。
さらに減圧していくと、液相は点③、気相は③’の点をとるというように、両者がグラフの左下へ移動していきます。
そして、気相の組成が仕込み比と同じになった点④’で、すべての分子が気体になったことになります。
その直前の液相の組成が点④になります。
これ以降は、すべて気相であるため、その組成は仕込み比のまま、点④’から見て真下の点⑤へ移ります。
グラフ中では、仕込み比\(z_\rm{A}\)を表す縦方向の直線を定組成線と呼びます。
また、平衡状態にある液相の組成と気相の点を結んだ線のことを連結線、英語ではtie lineと呼びます。
てこの規則
この連結線には、てこの規則というものが成り立ちます。

ある連結線について、定組成線との交点の左側の長さを\(l_\alpha\)、右側の長さを\(l_\beta\)とします。
それぞれの相の全物質量を\(n_\alpha\)、\(n_\beta\)とすると、\(n_\alpha l_\alpha=n_\beta l_\beta\)が常に成り立ちます。
証明はこのようになります。
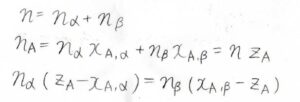
まず、全体の物質量\(n\)は\(n_\alpha+n_\beta\)です。
そして、\(\rm{A}\)の物質量は、\(n_\alpha x_{\rm{A}, \alpha}+n_\beta x_{\rm{A}, \beta}\)です。
これは、全物質量\(n\)と仕込み比\(z_\rm{A}\)の積とも書けます。
これを整理すると、\(n_\alpha (z_\rm{A}\)\(-x_{\rm{A}, \mathit{\alpha}})=n_\beta (x_{\rm{A}, \beta}-z_\rm{A})\)となります。
\(l_\alpha\)と\(l_\beta\)はそれぞれ\(z_\rm{A}\)\(-x_{\rm{A}, \alpha}、x_{\rm{A}, \beta}-z_\rm{A}\)に対応しています。
温度-組成図
ここで、先ほどは温度を固定して圧力を変化させていましたが、今度は圧力を固定して温度を変化させてみます。
温度を変化させると、それぞれの成分の飽和蒸気圧が変化することになります。
飽和蒸気圧と温度の関係は、以前紹介したクラウジウス-クラペイロンの式で書かれます。
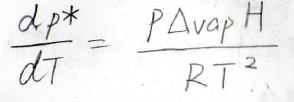
詳しくは、こちらを参照ください。
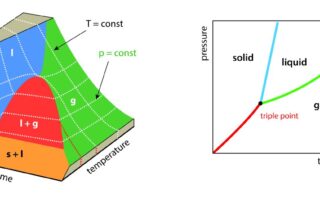
ここで\(\Delta_\rm{vap}\)\( H\)は蒸発エンタルピー、\(R\)は気体定数です。
基準の温度を\(T_0\)とすると、温度\(T\)における飽和蒸気圧\(p^\ast(T)\)は、\(\displaystyle p^\ast(T_0)\exp{[-\frac{\Delta_\rm{vap} \mathit{H}}{R}(\frac{1}{\mathit{T}}-\frac{1}{\mathit{T}_0})]}\)となります。
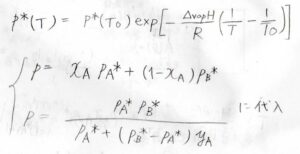
これを、先ほどの圧力と組成の関係式に代入し、温度について整理します。
ただし、ここでは蒸発エンタルピーの温度依存性を無視しています。
そのようにすると、こちらの右側のようなグラフになります。
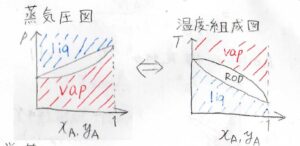
温度と組成の関係を表した図なので、温度-組成図と呼びます。
蒸気圧図との違いとして、液相がグラフの下側、気相がグラフの上側にあるという特徴があります。
液相1相状態から気相1相状態への変化は、先ほどとまったく同じように考えることができます。
仮に、溶質\(\rm{B}\)の揮発性が低いときには、溶液の温度を上げることで出てくる気体を集めて、それを凝縮し液体にすれば、純度の高い溶媒が得られます。
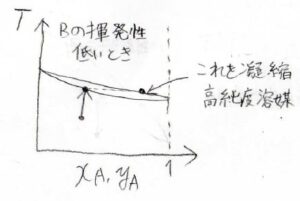
これを単蒸留といいます。
また、両方の成分が揮発性であったとしても、蒸留で集めてきた液体をさらに蒸留することで、純度を高めることができます。
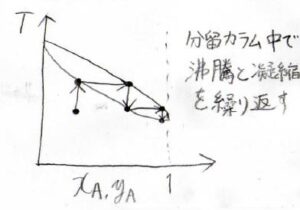
これを複数回行うことで2成分を分離させる操作のことを一般的に分別蒸留、もしくは分留といいます。
複数回といっても、実際に何回も蒸留の操作をするわけではなくて、分留カラムの中で蒸留を繰り返させることができます。
繰り返される蒸留の回数は、理論段数といいます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!