こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(ideal solution)
それでは内容に入っていきます!
単成分系気-液平衡状態
始めに、純粋な液体について化学ポテンシャルを考えます。
容器の中にある液体\(\rm{A}\)\(\)を入れて、平衡状態になるまで放置します。
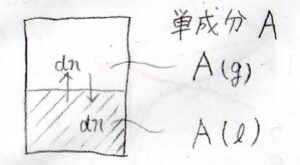
容器の中の空気は完全に取り除かれており、気相も純粋な\(\rm{A}\)\(\)の気体であるとします。
温度は標準温度としておきます。
純粋なときの化学ポテンシャルは\(\mu^\ast\)と表すことにします。
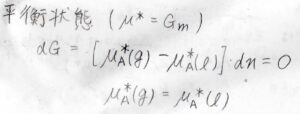
もちろんこれは、モルギブズエネルギーと等しいものです。
平衡状態では、それぞれの相の化学ポテンシャルは等しくなるため、\(\mu^\ast(\rm{g}\)\()=\mu^\ast(\rm{l}\)\()\)となります。
さらに気体が理想気体のときには、前回求めたとおり、化学ポテンシャルは圧力の関数として、このように書けます。
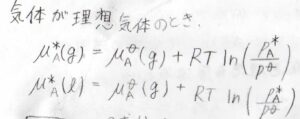
\(p^\circ\)は標準圧力、\(\mu^\circ\)は標準圧力における化学ポテンシャルもしくはモルギブズエネルギーで、標準化学ポテンシャルといいます。
\(R\)は気体定数、\(p^\ast\)は飽和蒸気圧です。
また、この値は液相の化学ポテンシャル\(\mu^\ast(\rm{l}\)\()\)と等しくなります。
標準圧力においても、2相それぞれの化学ポテンシャルは等しいので、液相の標準化学ポテンシャル\(\mu^\circ(\rm{l}\)\()\)を気相についての値\(\mu^\circ(\rm{g})\)として書いても問題ありません。
2成分系気-液平衡状態
では続いて、2成分系を考えてみましょう。
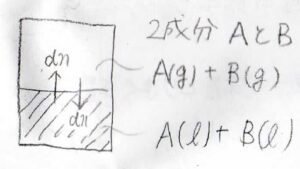
このとき、気相における\(\rm{A}\)\(\)の化学ポテンシャル\(\mu_\rm{A}\)\((\rm{g}\)\()=\mu^\circ(\rm{g}\)\()+RT\ln{(p_\rm{A}/\mathit{p}^\circ)}\)と書けて、この値は液相の化学ポテンシャル\(\mu_\rm{A}\)\((\rm{l}\)\()\)と等しくなります。
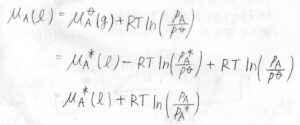
ただし、\(p_\rm{A}\)\(\)は気体\(\rm{A}\)\(\)の分圧です。
さらに\(\mu^\circ(\rm{g}\)\()\)を\(\mu^\ast(\rm{l}\)\()-RT\ln{(p_\rm{A}^\ast/\mathit{p}^\circ)}\)と書き換えると、\(p^\ast\)が消去できて、\(\mu_\rm{A}\)\((\rm{l}\)\()=\mu^\ast(\rm{l})\)\(+RT\ln{(p_\rm{A}/\mathit{p}^\ast)}\)となります。
つまり、\(\rm{A}\)\(\)の化学ポテンシャルは純粋なときの化学ポテンシャルと飽和蒸気圧を基準に、分圧によって求められるということです。
理想溶液
そして、混ざり合っている化合物の構造が、例えばベンゼンとトルエンのように似通っていた場合、次のような式がよく成り立つことが実験的に確かめられています。
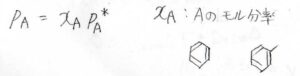
気体\(\rm{A}\)\(\)の分圧\(p_\rm{A}\)\(\)は、純粋な\(\rm{A}\)\(\)の飽和蒸気圧\(p_\rm{A}\)\(^\ast\)とモル分率\(x_\rm{A}\)\(\)の積として書けます。
この法則をラウールの法則といいます。
そして、あらゆる組成比、つまりモル分率が\(0\)から\(1\)までのどの値をとっていたとしても、すべての成分についてラウールの法則が成り立つ溶液のことを理想溶液と呼びます。
このとき、化学ポテンシャル\(\mu\)は、\(\mu^\ast(\rm{l}\)\()+RT\ln{x}\)で書けるということになります。
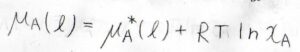
気体が理想気体であることは定義に含まれていないので、注意してください。
そして、ラウールの法則によって導かれる事実として、理想溶液の各成分は気化しにくくなるということがいえます。
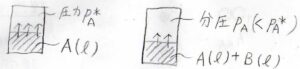
これは、混合により液相のエントロピーが増大することで、純粋なときに比べて液体であることが熱力学的に有利となるためです。
また、別の実験的事実として、その混合系の中で分率が\(1\)に近い成分があったときには、理想溶液でなくとも、その成分についてラウールの法則が成り立ちます。
この分子論的起源については、この記事の後半でお話しします。
そして、理想溶液全体のギブズエネルギー\(G\)は、\(\mu_\rm{A}\)\(n_\rm{A}\)\(+\mu_\rm{B}\)\(n_\rm{B}\)\(\)と書けるため、混合によるギブズエネルギー変化\(\Delta_\rm{mix}\)\(GはnRT(x_\rm{A}\)\(\ln{x_\rm{A}}+x_\rm{B}\)\(\ln{x_\rm{B}})\)となります。
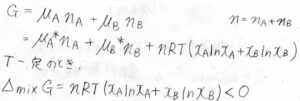
ここで\(n=n_\rm{A}\)\(+n_\rm{B}\)\(\)です。
この式は、理想気体の混合ギブズエネルギーとまったく同じ式です。
したがって、混合エントロピー、混合エンタルピー、混合による体積変化いずれも理想気体の結果と同じになります。
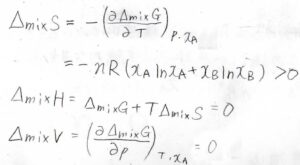
理想気体と理想溶液の違い
ここで、理想気体と理想溶液の違いを整理しておきます。
まず、理想気体、より厳密には完全気体というべきなのですが、これには分子間相互作用がありません。
これに対して、利用溶液は液体なので、分子間距離が近く、互いに相互作用があります。
ただ、純粋なときと混合したときでその相互作用に変化がなかったときには、混合エンタルピーが\(0\)になって、理想気体と同じ式で熱力学量変化が書けることになります。
図にするとこんな感じです。

2成分系における各分子間の相互作用エネルギーを、\(\rm{A}\)\(\)同士について\(h_\rm{AA}\)\(\)、\(\rm{B}\)\(\)同士について\(h_\rm{BB}\)\(\)、\(\rm{AB}\)\(\)間について\(h_\rm{AB}\)\(\)とします。
いま、分子の大きさの違いは考えていません。
理想溶液で考えているのは、\(h_\rm{AA}\)\(=h_\rm{AB}\)\(=h_\rm{BB}\)\(\)までであり、理想気体ではさらにこれらがすべて\(0\)になるということを考えています。
理想溶液とならない要因
理想溶液とならないパターンとしては、まずこれらの異種分子間相互作用が同種分子間相互作用と大きく異なるということが考えられます。

わかりやすいのが、水と油の組み合わせで、これらを混ぜようとしても、多くの場合は相分離します。
また、混合により錯体やもっと大きなネットワーク構造を形成する場合は、分子の配置に秩序ができるので、混合エントロピーも理想系の式からずれてきます。
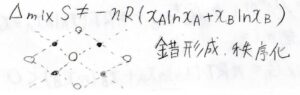
理想希薄溶液
では、理想溶液と実在溶液はどのような違いがあるのかを見ていきます。
次の2つのグラフは、横軸が\(\rm{A}\)\(\)のモル分率、縦軸が各成分の分圧と全圧を書いたものです。
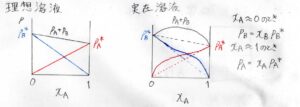
赤が\(\rm{A}\)\(\)の分圧、青が\(\rm{B}\)\(\)の分圧、黒が全圧です。
左が理想溶液、右が実在溶液のグラフです。
まず、左の理想溶液では、分圧がモル分率に比例するので、すべて直線のグラフになります。
対して、右の実在溶液では、このような曲線になります。ただし、前半でも言ったとおり、モル分率が\(1\)に近い成分については、ラウールの法則が成り立ちます。
つまり、\(x_\rm{A}\)\(=0\)付近で\(p_\rm{B}\)\(=x_\rm{B}\)\(p_\rm{B}\)\(^\ast\)となり、\(x_\rm{A}\)\(=1\)付近で\(p_\rm{A}\)\(=x_\rm{A}\)\(p_\rm{A}\)\(^\ast\)となります。
しかし実は、分率が\(0\)に近い成分についても、次のような比例関係が成り立つことが実験的に確かめられています。
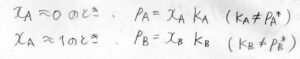
\(x_\rm{A}\)\(=0\)付近で\(p_\rm{A}\)\(=x_\rm{A}\)\(K_\rm{A}\)\(\)となり、\(x_\rm{A}\)\(=1\)付近で\(p_\rm{B}\)\(=x_\rm{B}\)\(K_\rm{B}\)\(\)となります。
この法則をヘンリーの法則といいます。
ここで、\(K_\rm{A}\)\(\)、\(K_\rm{B}\)\(\)は圧力と同じ次元をもつ比例定数で、飽和蒸気圧\(p_\rm{A}\)\(^\ast\)、\(p_\rm{B}\)\(^\ast\)とはそれぞれ異なる値となります。
この比例定数と飽和蒸気圧の差は、同種分子間、異種分子間の相互作用の差を反映しています。
溶媒についてラウールの法則が成り立ち、溶質についてヘンリーの法則が成り立つほど濃度が低い溶液のことを、理想希薄溶液といいます。
ここで、溶媒とは分率が大きい成分、溶質とは分率が小さい成分のことを指しています。
法則の分子論的解釈
最後に、ラウールの法則、ヘンリーの法則の分子論的起源について、お話しして終わります。
両者の違いを考えるために、1個の分子とそのまわりの環境を考えます。
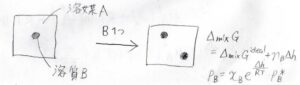
その着目している分子とは異なる成分を添加していったとしても、分子をとりまく環境が純粋なときと大きく変わらないとき、ラウールの法則が成り立ちます。
自身とは異なる成分と構造が似ているとき、もしくは分率が\(1\)に近いときに、このような状態になります。
対して、ヘンリーの法則ですが、まず全体の混合エンタルピーが溶質分子の個数に比例します。
いま、\(\rm{B}\)\(\)の周りがすべて\(\rm{A}\)\(\)だったときの分子1個あたりエンタルピー変化を\(\Delta h\)とします。
すると、ギブズエネルギー変化は、理想溶液の値から\(n_\rm{B}\)\(\Delta h\)だけ大きくなったことになります。
これを変形すると、分圧がモル分率に比例するのは変わりませんが、飽和蒸気圧が見かけ上大きくなった形になります。
したがって、比例定数が変化した形で比例関係が成り立つことになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!